自动搬运

查看原文

来自洛谷，原作者为

	ComplexPlanck 这个家伙没留下什么，什么都没留下

搬运于2025-08-24 22:34:52，当前版本为作者最后更新于2022-07-25 17:31:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题面非常简洁，注意到一次操作之后，$\,a_{i}\,$的值会变为$\,a_{a_{i}}\,$，所以我们不妨建立一张图，并连出$\,a_{i}\rightarrow i\,$的边。

画出这样一张图之后，你会发现这张图有$\,n\,$个点$\,n\,$条边，由于可能存在自环，所以这张图是基环树森林（其中可能存在环是自环的基环树）

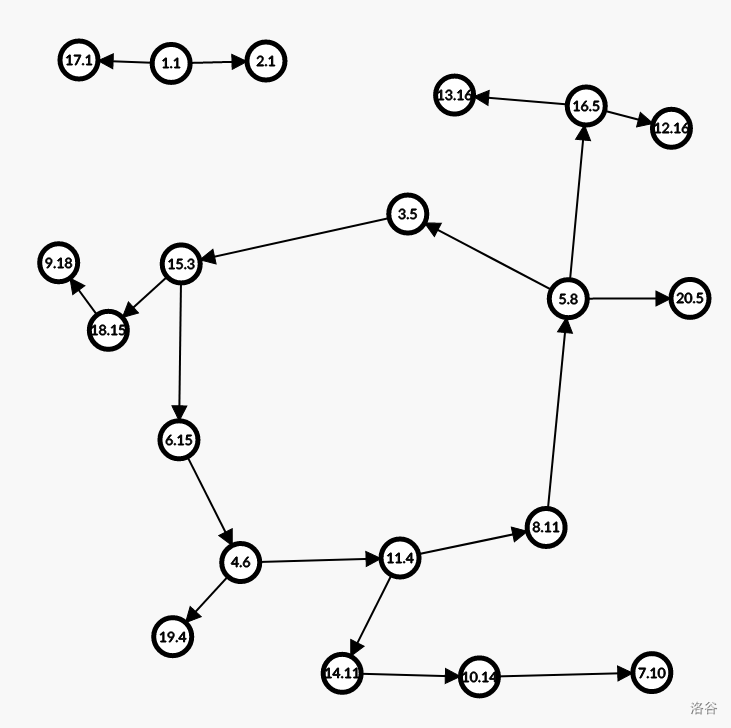
（样例 2 的图，$\,x.y\,$表示序号为$\,x\,$，$\,a_x\,$的值为$\,y\,$的点，自环 Graph Editor 画不出来...）

并且显然的，这是一个内向树森林，所有点的入度都为$\,1\,$，定义对于边$\,u\rightarrow v\,$，$\,u\,$为$\,v\,$的父亲，注意父亲可能是自己。

注意到这样一个事实：

第一次操作后，$\,a_{i}\,$的值会变为$\,a_{a_{i}}\,$；

第二次操作后，$\,a_{i}\,$的值会变为$\,a_{a_{a_{a_{i}}}}\,$（有$\,4\,$个$\,a\,$）；

第$\,r\,$次操作之后，$\,a_{i}\,$的值会变为

（不知道看不看得清）总之就是有$\,2^{r}\,$个$\,a\,$，相当于是从点$\,i\,$开始，跳到父亲$\,2^r\,$次。

我们不妨对基环树的环和附属子树（设$\,i\,$是环上的点，那么断开其在环上的边，剩下的是一棵树，称其为附属子树）分开讨论。

先讨论附属子树，由于附属子树树高不超过$\,\mathcal{O}(n)\,$，所以对于附属子树上的点，至多只需要$\,\mathcal{O}(\log n)\,$次就能跳到环中。

所以我们可以先跳$\,\left\lceil\log_{2}n\right\rceil\,$次，这样基环树森林的附属子树的高都变为$\,0\,$或$\,1\,$了。高为$\,0\,$的附属子树不用管，对于高为$\,1\,$的附属子树，此时的$\,a_{i}\,$是$\,i\,$下一步要跳到的点，假设$\,ans[p]\,$为点$\,p\,$最终跳到的点，$\,pre[p]\,$为跳到$\,p\,$的点上一步跳到的点，那么点$\,i\,$最终跳到的点就是$\,pre[ans[a_i]]\,$。

那么我们现在只需要处理环以及$\,pre\,$数组就行了。

由于我们之前已经跳过$\,\left\lceil\log_{2}n\right\rceil\,$次，所以接下来我们只需要跳$\,2^{k-\left\lceil\log_{2}n\right\rceil}\,$就够了，假设环长为$\,leng\,$，那么显然每个点只需要跳$\,2^{k-\left\lceil\log_{2}n\right\rceil}\operatorname{mod}leng\,$次就够了。

注意这里不能每个点都跳这么多次，因为这显然对于每个点，最坏是$\,\mathcal{O}(leng)\,$的，最坏复杂度可能到达$\,\mathcal{O}(n^2)\,$，所以我们不妨钦定一个起点$\,st\,$，我们让$\,st\,$跳这么多次就够了，假设最后跳到$\,ed\,$，因为$\,st\,$的后一个点最终跳到的位置显然是$\,ed\,$的后一个点，递推即可，这是$\,\mathcal{O}(1)\,$的。

显然在递推的过程中，我们可以顺带处理出$\,pre\,$数组，所以这个问题我们也解决了。

至此，这道题的流程就结束了，瓶颈在于那个快速幂，总体上时间复杂度是$\,\mathcal{O}(n\log k)\,$的，可以通过，具体实现可以看带注释的代码。

#include <bits/stdc++.h>

namespace io
	// 省略快读快写
using namespace io;
namespace problems
{
	const int N = 500010;
	int n, k;
	int a[N], b[N], ans[N], pre[N];
	bool vis[N];
	int idc[N], cidx = 0, large;

	void go(void)
	{
		for (int i = 1; i <= n; ++ i)
			b[i] = a[a[i]];
		for (int i = 1; i <= n; ++ i)
			a[i] = b[i];
		return;
	}
	int ksm(int a, int b, int p)
	{
		int res = 1;
		while (b)
		{
			if (b & 1) res = 1ll * res * a % p;
			a = 1ll * a * a % p, b >>= 1;
		}
		return res;
	}

	int main(void)
	{
		memset(vis, false, sizeof(vis));

		read(n), read(k);
		for (int i = 1; i <= n; ++ i)
			read(a[i]);
		int lgn = log2(n) + 1;
		while (lgn && k)
		{
			-- lgn, -- k;
			go();
		}
		if (!k)
		{
			for (int i = 1; i <= n; ++ i)
				writesp(a[i]);
			puts(""); return 0;
		}
		for (int i = 1; i <= n; ++ i)
			if (!vis[i])
			{
				int now = i;
				for ( ; !vis[now]; now = a[now])
					vis[now] = true;
				// 找环
				if (idc[now]) continue;
				// i 是附属子树上的点，找到了旧环
				++ cidx, large = 0;
				int st = now;
				for ( ; !idc[now]; now = a[now])
					idc[now] = cidx, pre[a[now]] = now, ++ large;
				// 给环编号
				int times = ksm(2, k, large);
				// 需要偏移 2^k 次，模数为环长 large
				now = st;
				while (times --)
					now = a[now];
				ans[st] = now;
				// 找到起点对应的位置
				int x = st, y = now;
				x = a[x], y = a[y];
				while (x != st)
				{
					ans[x] = y;
					x = a[x], y = a[y];
				}
				// 将环上的点的答案处理掉
			}
		for (int i = 1; i <= n; ++ i)
			if (!idc[i])
			// 处理附属子树
				ans[i] = pre[ans[a[i]]];
		for (int i = 1; i <= n; ++ i)
			writesp(ans[i]);
		puts("");

		return 0;
	}
}

int main(void)
{
	problems::main();

	return 0;
}