1 条题解
-
0
自动搬运
来自洛谷,原作者为

Math_rad_round
旋转卡壳有2^4种读法,你知道吗?||NOIP退役苕皮搬运于
2025-08-24 22:34:49,当前版本为作者最后更新于2021-11-28 16:09:56,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
我们把这道题直观化。
可以将数列想象成二维地图, 就是在 位置上的山的高度。自然我们到不了山里(你的行数 不小于 )。
向左上、正上、右上花费 ;向左,右花费 ;左下、正下、右下花费 。
样例说明这幅图就挺合适。
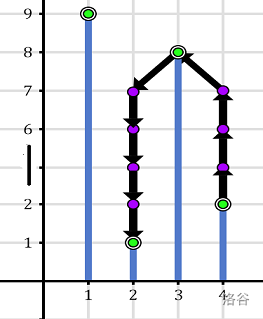
对于一个询问,我们可以先认为 。
这样,我们水平移动的次数就决定好了,因此我们应当尽量的利用水平移动的步数向上(向下)走。
对于 来说,我们让他尽量向右上走,这样它的轨迹就是一条斜率为 的直线(下图红色)。
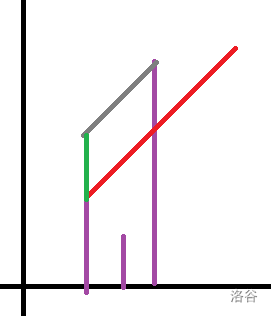 (紫色的是山)
(紫色的是山)显然我们可以发现,等到撞上墙了再往上升,不如再起点处就向上。(绿+灰)
那我们要预先向上多少个呢?根据上图,我们可以看出这个值是:
即:
因此我们只需要维护一个 的 即可得到答案。
从 开始向左也是类似,维护 。
但是,这并没有结束,如下图所示,显然不能从 一路向右走到 。
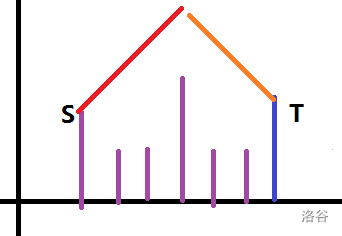
因此我们在得到 以后,还要知道 (可以发现 )。
然后我们就可以知道路径了。
从 向上;然后一路斜上至 ,斜上到与 平高;向右经过 到一个合适的位置;向右下经过 一直斜下 那一列;向下到 。

至于具体长度我相信各位看懂上一幅图也不会有难度。
剩余的就是细节问题了,对于 可以先交换 ,然后把上升和下降的费用对调。同时注意本题必须开 。
用ST表实现最大值维护的话时间复杂度 ,空间 。
代码:
#include<iostream> int n; #define he(i,j) (h[st[i][j]]+st[i][j]) #define eh(i,j) (h[ts[i][j]]+n-ts[i][j]) #define hh(i,j) (h[tt[i][j]]) #define ll long long using namespace std; ll st[300000][20]; ll ts[300000][20]; ll tt[300000][20]; ll d[300000]; ll h[300000]; ll maxnn(ll a,ll b){ if(a==b)return ts[a][0]; ll le=b-a+1;ll o=(b-(1<<d[le]))+1; if(he(a,d[le])>he(o,d[le])){ return st[a][d[le]]; }else return st[o][d[le]]; } ll maxn(ll a,ll b){ if(a==b)return st[a][0]; ll le=b-a+1;ll o=b-(1<<d[le])+1; if(eh(a,d[le])>eh(o,d[le])){ return ts[a][d[le]]; }else return ts[o][d[le]]; } ll maxt(ll a,ll b){ if(a==b)return tt[a][0]; ll le=b-a+1;ll o=b-(1<<d[le])+1; if(hh(a,d[le])>hh(o,d[le])){ return tt[a][d[le]]; }else return tt[o][d[le]]; } ll len(ll a,ll b,ll f){//这里我是直接分别求这四段的路径长度 if(a==b)return 0;//和题解不同 ll ans=0; ans+=(b-a)*2; if(h[a]<h[b]){ ans+=(h[b]-h[a])*(2-3*f); if(h[b]-h[a]>b-a)ans+=(h[b]-h[a]-(b-a))*1LL*2; }else{ ans+=(h[a]-h[b])*(-1+3*f); if(h[a]-h[b]>b-a)ans+=(h[a]-h[b]-(b-a))*1LL*2; } return ans; } int main(){ ll q; cin>>n; for(ll i=1;i<=n;i++){ cin>>h[i]; st[i][0]=ts[i][0]=tt[i][0]=i; } for(ll i=1;i<=19;i++){//三个ST表 ll le=1<<(i-1); for(ll j=1;j+le*2-1<=n;j++){ if(he(j,i-1)>he(j+le,i-1)){ st[j][i]=st[j][i-1]; }else st[j][i]=st[j+le][i-1]; if(eh(j,i-1)>eh(j+le,i-1)){ ts[j][i]=ts[j][i-1]; }else ts[j][i]=ts[j+le][i-1]; if(hh(j,i-1)>hh(j+le,i-1)){ tt[j][i]=tt[j][i-1]; }else tt[j][i]=tt[j+le][i-1]; } } ll le=0,g=1; for(ll i=1;i<=n;i++){//预处理对数 if(2*g<i){ le++;g*=2; }d[i]=le; }cin>>q; for(ll i=1;i<=q;i++){ ll a,b;cin>>a>>b; ll lo=0; if(a>b){ swap(a,b);lo=1; } ll yg=maxnn(a,b),zg=maxn(a,b); ll zz=maxt(zg,yg); // cout<<a<<" "<<zg<<" "<<zz<<" "<<yg<<" "<<b<<endl; ll ans=0; ans+=len(a,zg,lo); ans+=len(zg,zz,lo); ans+=len(zz,yg,lo); ans+=len(yg,b,lo); cout<<ans<<endl; } return 0; }
- 1
信息
- ID
- 7316
- 时间
- 2000ms
- 内存
- 256MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
