自动搬运

查看原文

来自洛谷，原作者为

	AsunderSquall The cruelest fate is to have hope and see it crushed before your eyes.

搬运于2025-08-24 22:34:36，当前版本为作者最后更新于2021-11-17 19:51:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

逆转比特

题意

一个点在长为 $n$ 的 只含有 0/1 的序列上随机游走（下标从 1 开始），点的初始坐标为 $p$，重复进行以下操作：

• 1. 当序列全为一种字符时，停止操作；
• 2. 记点当前位置 $p$，等概率随机选择一个点 $q$，把点移动到 $q$，将 $q$ 处的字符的取反，总代价加上 $f(|p-q|)$，这里 $f(x)=Ax^2+Bx$，其中 $A,B$ 是两个给定常数；
• 3. 回到第一条。

你需要进行 $q$ 次修改，具体而言，每次修改包括

• 1. 将序列第 $\mathit{idx}$ 位的 0/1 翻转；
• 2. 查询初始坐标为 $p$ 时，停止操作后的期望代价。

注意，一旦修改一直有效。

你需要输出 $q$ 次询问期望代价模 $998244353$ 的结果的异或和。

题解

下述先考虑单组询问， 用 $s$ 表示 01 串，$p$ 表示点的位置。

算法一

我会暴力高斯消元！

一个显然的做法类似随机游走，在 $n 2 ^ n$ 种状态（01 串形态与点的位置）中列出线性方程组，直接高斯消元解出变量，这样做复杂度 $O(8^nn ^ 3)$。

期望得分：5。

算法二

我会期望的线性性！

上述做法很大的缺陷是状态数太多。注意到 $i$ 走到 $j$ 的代价是固定的，并且只与 $|i-j|$ 有关，枚举所有的 $i\neq j$ 计算 $i\rightarrow j$ 的期望次数 $E_{i\rightarrow j}$，

$$ans=\sum_{i=1}^n\sum_{j=1}^n[i\neq j]f(|i-j|)E_{i\rightarrow j} $$

对于一组$i,j$，有效信息只有

• $r = \sum_{k = 1} ^ n [s_i = s_k]$
• $u = [p = i]$
• $v = [s_i = s_j]$

有效信息可用三元组 $(r,u,v)$ 表示，只有 $O(n)$ 种，直接高斯消元，一组 $(i,j)$ 就可以 $O(n^3)$。冷静一下，所有 $i\neq j$ 不需要分开求，合起来列方程求解就可以，此时总复杂度 $O(n^3+qn^2)$。

按照点移到 $i,j$，其他位置的 $0$，其他位置的 $1$ 四种情况分类讨论转移及系数，具体转移如下：

$$\begin{aligned} f(a, 0, 0)&= \frac{1}{n} f(n - a + 1, 1, 1) + \frac{a - 1}{n} f(a - 1, 0, 0)\\ &+ \frac{1}{n} f(a + 1, 0, 1) + [a < n] \frac{n - a - 1}{n} f(a + 1, 0, 0)\\ f(a, 1, 0)&= \frac{1}{n} f(n - a + 1, 1, 1) + \frac{a - 1}{n} f(a - 1, 0, 0)\\ &+ \frac{1}{n} (f(a + 1, 0, 1) + 1) + [a < n] \frac{n - a - 1}{n} f(a + 1, 0, 0)\\ f(a, 0, 1) &= \frac{1}{n} f(n - a + 1, 1, 0) + \frac{1}{n} f(a - 1, 0, 0)\\ &+ [a > 1]\frac{a - 2}{n} f(a - 1, 0, 1) + \frac{n - a}{n} f(a + 1, 0, 1)\\ f(a, 1, 1) &= \frac{1}{n} f(n - a + 1, 1, 0) + \frac{1}{n} (f(a - 1, 0, 0) + 1)\\ &+ [a > 1]\frac{a - 2}{n} f(a - 1, 0, 1) + \frac{n - a}{n} f(a + 1, 0, 1)\\ \end{aligned} $$

（其实这些方括号都是不需要的，因为这些不合法的状态前面系数都为 $0$，不妨设其值也为 $0$）

由于要做大小为 $4n \times 4n$ 的矩阵的高斯消元，所以常数很大不能忽略。

期望得分：23。

算法三

我会观察性质！

仔细观察，容易发现，在 $a$ 不为 $n$ 的时候，$f(a, 1, b) = f(a, 0, b) + \frac{1}{n}$，由此 $(r,v)$ 才是有效的，只有 $2n$ 种。

这个观察非常容易所以没有给这一档部分分。（除非你是松怪用它过了 Subtask 3）

$$\begin{aligned} f(a, 0)&= \frac{1}{n} f(n - a + 1, 1) + \frac{a - 1}{n} f(a - 1, 0)\\ &+ \frac{1}{n} f(a + 1, 1) + \frac{n - a - 1}{n} f(a + 1, 0) + \frac{1}{n ^ 2}\\ f(a, 1) &= \frac{1}{n} f(n - a + 1, 0) + \frac{1}{n} f(a - 1, 0)\\ &+ \frac{a - 2}{n} f(a - 1, 1) + \frac{n - a}{n} f(a + 1, 1) + \frac{1}{n ^ 2}\\ \end{aligned} $$

特别的，当 $a=1$ 时，没有 $\frac 1 {n^2}$ 项。

记 $g(a) = f(a, 0) - f(a, 1)$，显然只有 $1<a<n$ 的时候该式有意义。
但是考虑到，式子中涉及到 $g(1)$ 和 $g(n)$ 前面的系数均为 $0$，所以不妨设其为 $0$。 两式相减得

$$ng(a)+g(n-a+1)=(a-2)g(a-1)+(n-a-1)g(a+1)(1<a<n)$$

可以证明 $\forall 1<a<n,g(a)=0$。

---

证明：

记 $g(k)-g(n+1-k)$ 为 $S(k)$。

考察 $a=k$ 和 $a=n+1-k$ 的情况，注意到

$$\begin{aligned} ng(k)+g(n+1-k)&=(k-2)g(k-1)+(n-1-k)g(k+1)\\ ng(n+1-k)+g(k)&=(k-2)g(n+2-k)+(n-1-k)g(n-k) \end{aligned} $$

两式相减得

$$(n-1)S(k)=(k-2)S(k-1)+(n-1-k)S(k+1)$$

稍微整理得好看一点

$$(n-k-1)S(k+1)-(k-1)S(k)=(n-k)S(k)-(k-2)S(k-1)$$

令 $A(k)= (n-k)S(k)-(k-2)S(k-1)$，我们得到 $A(k+1)=A(k)$。

考虑 $(n-1)S(2)=(n-3)S(3)$，有

$$A(3)=(n-3)S(3)-S(2)=(n-2)S(2)$$ $$(n-k)S(k)=(n-2)S(2)+(k-2)S(k-1)$$

可以看出所有 $S(a)$ 的正负性相同。

考虑到 $S(a)+S(n+1-a)=0$，因此只能所有 $S(a)=0$。 由此证明了 $\forall 1<a<n,g(a)=g(n+1-a)$。

思考一个问题，为什么我们列出了一个期望的方程丢进高斯消元里，他一定有解？

因为他的解确实存在，而且我们给出的方程可以描述整个问题。

$$\begin{aligned} ng(a)+g(n-a+1)&=(a-2)g(a-1)+(n-a-1)g(a+1)\\ (n+1)g(a)&=(a-2)g(a-1)+(n-a-1)g(a+1)\\ g(a)&=\dfrac{(a-2)g(a-1)+(n-a-1)g(a+1)}{n+1} \end{aligned} $$

这东西看着就很像一个期望的方程组，我们随便给他赋一个组合意义。
比如一个人在 $2 \sim n-1$ 的数轴上随机游走，然后有一定概率往左/往右/螺旋升天。
这个人走到任何一个位置都会获得 $0$ 的贡献，问从某个位置出发的期望贡献和，答案显然是 $0$。

不过其实也可以大眼观察法看出来。

---

有效状态压缩至 $n$ 个，设 $h_a = f(a, 0) = f(a, 1)$ 则有:

$$h_a = \frac{1}{n} h_{n - a + 1} + \frac{a - 1}{n} h_{a-1} +\frac{n - a }{n} h_{a + 1} + \frac{1}{n^2} $$

或者也可以对 $g$ 高斯消元，再回带回 $f$ 中高斯消元，相当于是解 $2$ 个 $n \times n$ 的方程组，常数会大一点，但应该能过 Subtask 3。

期望得分：35。

算法四

考虑一个常见技巧，如果 $h_a$ 只与 $h_{a-1}$ 与 $h_{a+1}$ 有关，可以把所有变量表示为 $h_i=k_ih_1 + b_i$ 的形式，列出一个等式求出$h_1$，从而推出全部 上面的式子中 $h_a$ 还与 $h_{n+1-a}$ 有关，有关系的点连边之后形成梯子状结构。
以下是 $n=8$ 时的一个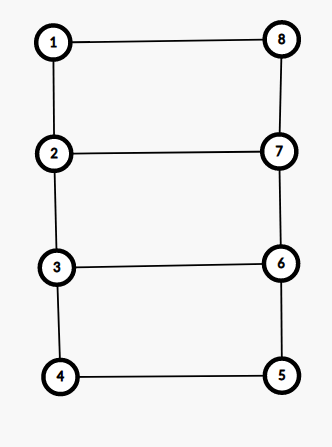例子：

类似上面做法，设 $h_1=x, h_{n-1}=y$，将 $h_i$ 表示为 $Ax + By + C$ 的形式，列出两个线性无关的额外方程解出 $x, y$。

值得注意的是这个方法在 $n \le 2$ 的时候会出问题，这就是为什么数据范围中 $n \ge 3$。

预处理已经可以线性，考虑询问。

$$\begin{aligned} ans &= \sum_{i = 1} ^ n \sum_{j=1, j \neq i}^n f(|i - j|) \cdot E_{i\rightarrow j}\\ &= \sum_{i = 1} ^ n \sum_{j = 1, j \neq i} ^ n f(|i - j|) \cdot ([p = i]\frac{1}{n} + h(\sum_{k = 1} ^ n [s_i = s_k])) \end{aligned} $$

需要注意如果 $a$ 全部相等需要加特判，由于大数据随机不到所以选择了添加子任务依赖关系。

预处理 $d_i=\sum_{j=1}^n f(|i-j|)$，单次询问做到 $O(1)$ 不成问题。

至此，复杂度 $O(n + q)$，期望得分：100。