自动搬运

查看原文

来自洛谷，原作者为

	耶梦加得 In the end it doesn't even matter.

搬运于2025-08-24 22:34:18，当前版本为作者最后更新于2021-11-22 22:32:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

不清楚是不是正解反正能过

分析问题

这个题可能乍一看很高大上排列，同构，字典序 blablabla

然而我们稍微模拟一下，很容易建立出一个更直观的模型

给这个树的节点填上 $1-n$ 的数字，让它成为一个小根堆，并且把这些数字按照某个 dfs 序排列能够使得字典序最大。

我怀疑那个样例故意往图上填下标就是为了不让这个模型太过明显

（接下来我们以 $a[x]$ 指代标号为 $x$ 的节点上写的数字）

首先堆顶肯定是 $1$，接下来我们希望第二个遍历到的数字尽可能大，有没有可能第二个数字是 $n$ 呢？根据样例显然有可能

$n$ 已经是最大的数了，这又是一个小根堆，那么它不能有任何子节点。也就是说我们希望这个根有一个子节点是叶子节点，子树大小为 $1$。

我们进一步推广这个结论，容易发现，假如当前还没写上去的最大的数是 $mx$，当前节点为 $x$ 子树大小为 $sz[x]$，由于我们必须先写上 $sz - 1$ 个数，满足它们比 $a[x]$ 更大，所以 $a[x] \le mx - sz + 1$。

那么对于任何一个局面，$mx$ 固定，根据字典序的比较规则，我们贪心地希望 $a[x]$ 最大，那么就需要 $sz[x]$ 最小。

如果一样呢？

那就递归处理（雾）。

此时问题变成了两个固定了根的子树 （否则就是递归到原问题原地爆炸） ，选一个字典序大的排在前面。我们可以归纳地处理这个问题。

我们比较的不再是 $sz[x]$，而是一个由若干 sz 值构成的序列 $f[x]$。这个序列的构造，使得我们可以通过比较两个子节点的 $f[x]$ 的字典序，判断它们在 dfs 序中的先后。

算了太绕了我们直接举例子吧

手写丑图预警，轻喷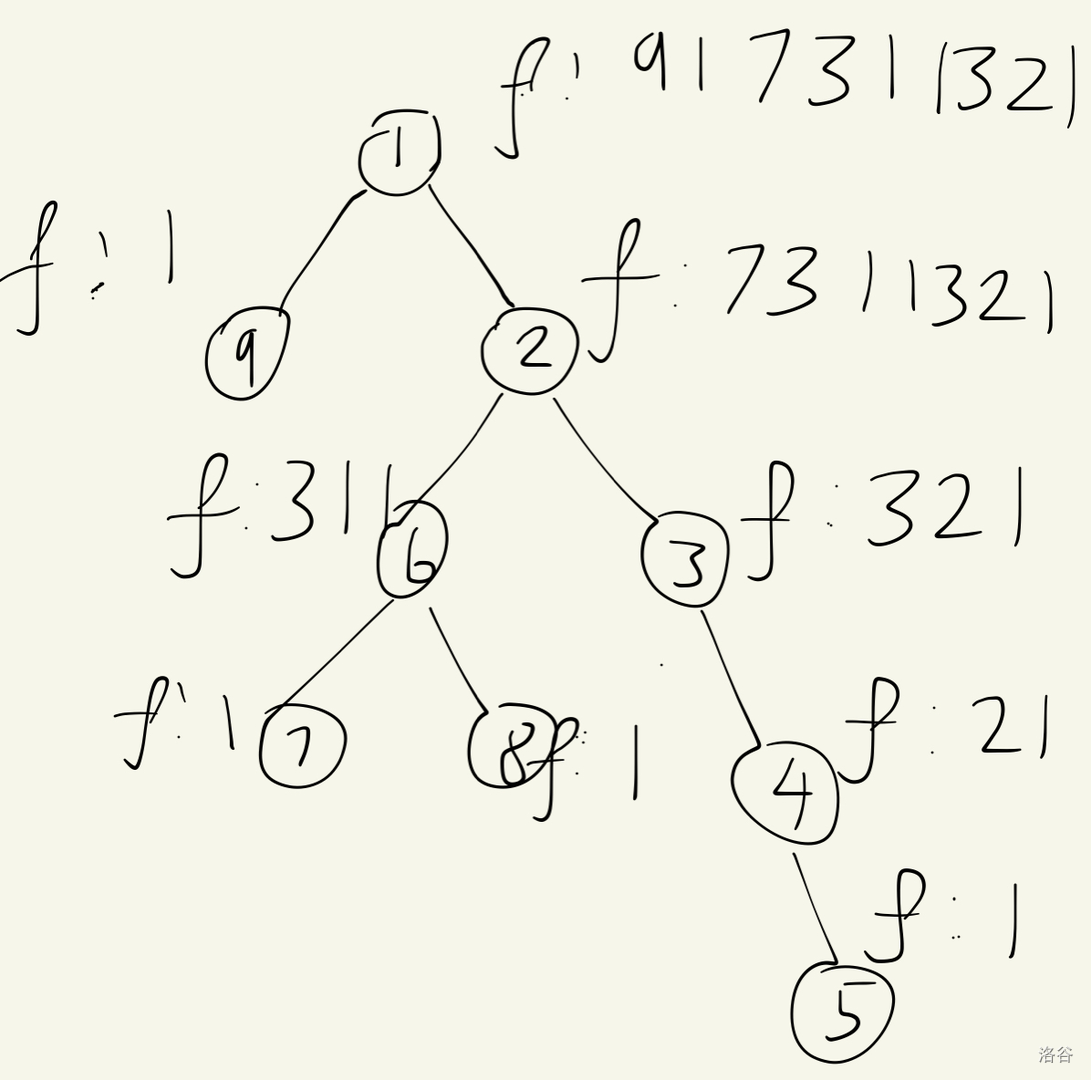

圆圈内是我们填上的数（而非标号），这个图最终得到的序列是 1 9 2 6 8 7 3 4 5

大概能懂这个 $f$ 序列是什么意思了吧

由于我们优先考虑 $sz[x]$，因此 $f[x]$ 的首项就是 $sz[x]$，接下来是按 dfs 序的 $sz[v]$ （$v$ 为 $x$ 后代），具体实现时我们可以直接把它的儿子的 $f[x]$ 按照 dfs 序拼接起来（容易证明二者等价）。

算法本身正确性由字典序的贪心性可以感性理解一下。

定根时的 DP 解法

vector<int> g[5007], f[5007];
int fa[5007];
inline bool cmp(int x, int y) {
    bool flag = true;
    if(f[x].size() > f[y].size()) {swap(x, y); flag = false;}
    for(int i = 0; i < f[x].size(); ++i) {
        if(f[x][i] < f[y][i]) return flag;
        if(f[x][i] > f[y][i]) return !flag;
    }
    if(f[x].size() < f[y].size()) return flag;
    return !flag;
}
int sz[5007];
int n;
void dfs1(int x) {
    sz[x] = 1; f[x].clear();
    for(int i = 0; i < g[x].size(); ++i) {
        if(g[x][i] != fa[x]) {
            fa[g[x][i]] = x;
            dfs1(g[x][i]);
            sz[x] += sz[g[x][i]];
        }
    }
    f[x].push_back(sz[x]);
    sort(g[x].begin(), g[x].end(), cmp);
    for(int i = 0; i < g[x].size(); ++i) {
        int k = g[x][i]; if(k == fa[x]) continue;
        for(int j = 0; j < f[k].size(); ++j) {
            f[x].push_back(f[k][j]);
        }
    }
}

由于 $|f[x]| = sz[x]$，易证所有 $f[x]$ 的总长度小于 $n^2$，那么瓶颈在于 sort 这一行上。

对于一个点 $u$ 和它的所有儿子 $v$，令 $u$ 有 $w$ 个儿子，那么比较次数是 $O(w \log w)$ 的。而单次比较的操作次数最多为两者 $f[x]$ 长度（亦即 $sz[x]$）的较小值。不严谨地说，我们总的操作次数应该不会超过（且实际上远小于）：

$\sum\overline{sz[v]}wlogw \approx \sum sz[x] logn = \sum n^2logn$

（欢迎各位大佬在评论区留言给出更严谨的说明 wtcl）

好了细心的同学可能已经发现了，我们写的是 dfs1

那势必有 dfs2

开始换根

不难发现如果我们对每个节点都作为根跑一次 dfs1 势必会 T

换根的思维难度不高，然而我自己的实现丑的要死

假设此时我们处理好了 $fa[x]$ 为根时的信息，那么我们把 $x$ 换成根，我们就要把 $fa[x]$ 旋下来，重新更新一遍信息。

暴力地遍历 $fa[x]$ 的儿子（我们已经排好序了），遇到不是 $x$ 的就合并。

但是停一下！在此之前，要二分地查找 $fa[fa[x]]$ 作为 $fa[x]$ 的儿子该塞在哪个位置，然后才能开始合并。

（由于我们似乎不能破坏已经排序好的数组，所以我只能用这种方式粗暴地解决问题）

然后我们故技重施，暴力查找 $fa[x]$ 应该扔在哪里，然后遍历 $x$ 的儿子，合并。

由于前面 cmp 函数写丑了所以这里会有一些 n + 2, n + 3 之类的数，本身并没有特别的意义。

int ansi;
vector<int> F[5007];
void dfs2(int x) {
    F[fa[x]].clear(); F[fa[x]].push_back(n - sz[x]);
    f[n + 3] = F[fa[fa[x]]];
    int pos = lower_bound(g[fa[x]].begin(), g[fa[x]].end(), n + 3, cmp) - g[fa[x]].begin();
    for(int i = 0; i < pos; ++i) {
        if(g[fa[x]][i] == x || g[fa[x]][i] == fa[fa[x]])continue;
        for(int j = 0; j < f[g[fa[x]][i]].size(); ++j) {
            F[fa[x]].push_back(f[g[fa[x]][i]][j]);
        }
    }
    for(int j = 0; j < F[fa[fa[x]]].size(); ++j) {
        F[fa[x]].push_back(F[fa[fa[x]]][j]);
    }
    for(int i = pos; i < g[fa[x]].size(); ++i) {
        if(g[fa[x]][i] == x || g[fa[x]][i] == fa[fa[x]])continue;
        for(int j = 0; j < f[g[fa[x]][i]].size(); ++j) {
            F[fa[x]].push_back(f[g[fa[x]][i]][j]);
        }
    }
    f[n + 3] = F[fa[x]]; f[n + 2].clear(); f[n + 2].push_back(n);
    pos = lower_bound(g[x].begin(), g[x].end(), n + 3, cmp) - g[x].begin();
    for(int i = 0; i < pos; ++i) {
        if(g[x][i] == fa[x])continue;
        for(int j = 0; j < f[g[x][i]].size(); ++j) {
            f[n + 2].push_back(f[g[x][i]][j]);
        }
    }
    for(int j = 0; j < F[fa[x]].size(); ++j) {
        f[n + 2].push_back(F[fa[x]][j]);
    }
    for(int i = pos; i < g[x].size(); ++i) {
        if(g[x][i] == fa[x])continue;
        for(int j = 0; j < f[g[x][i]].size(); ++j) {
            f[n + 2].push_back(f[g[x][i]][j]);
        }
    }
    if(cmp(n + 2, n + 1)) {
        ansi = x; f[n + 1] = f[n + 2];
    }
    for(int i = 0; i < g[x].size(); ++i) {
        if(g[x][i] != fa[x]) dfs2(g[x][i]);
    }
}

完结撒花！

gg，我们还没有输出

int ans[5007];
void dfs(int x) {
    static int cnt = 0;
    ans[x] = ++cnt;
    for(int i = g[x].size() - 1; i >= 0; --i) {
        if(g[x][i] == fa[x]) continue;
        dfs(g[x][i]);
    }
}
void sfd(int x) {
    printf("%d ", ans[x]);
    for(int i = 0; i < g[x].size(); ++i) {
        if(g[x][i] == fa[x]) continue;
        sfd(g[x][i]);
    }
}
signed main() {
    scanf("%d", &n);
    for(int i = 1; i < n; ++i) {
        int a, b; scanf("%d %d", &a, &b);
        g[a].push_back(b); g[b].push_back(a);
    }
    dfs1(1); ansi = 1;
    f[n + 1] = f[1];
    for(int i = 0; i < g[1].size(); ++i) dfs2(g[1][i]);
    fa[ansi] = 0; dfs1(ansi);
    dfs(ansi); sfd(ansi);
    return 0;
}

（两个 dfs 用来输出看上去不太优雅，但是它能解决这道题）