自动搬运

查看原文

来自洛谷，原作者为

	MuYC 这个人蠢爆了，但是他是 ZHY 的耶耶

搬运于2025-08-24 22:33:59，当前版本为作者最后更新于2021-10-06 17:49:46，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Solution

线段树合并 + 线段树二分。

设 $f_u$ 表示所有完全在 $u$ 子树内并包含 $u$ 的连通点集，权值之和最大的是多少。

那么有 $f_u = \displaystyle \sum_{v \ is \ u's \ son} f_v [f_v \ge 0]$。

考虑从小到大枚举 $x$ 的过程中，一定存在一个最小的 $x$ 使得 $f_{u} \ge 0$，我们设对于 $u$ 这个最小的 $x$ 为 $t_u$。

很显然，对于一个叶子节点来说，$t_u = -val_u$，任意一个 $t_u$ 均可以通过二分得到，不妨假设我们现在二分到的值是 $k$。

注意这样一个事实：

当 $v$ 是 $u$ 的子树中的节点的时候，必然已经求得了 $t_v$。那么设 $u$ 到 $v$ 的路径上的所有点对应的 $t$ 的最大值为 $t_{max}$ 的话：

那么当 $k \ge t_{max}$ 的时候，这个 $v$ 就会对于 $u$ 造成贡献，这个贡献的值就会是 $k + val$ 。

于是可以想到开一棵线段树，以 $t_u$ 为下标，节点 $[l,r]$ 里面存 $\sum val$ 以及 $cnt$ ，其中 $\sum val$ 表示 $t$ 落在区间 $[l,r]$ 中的点的和，$cnt$ 即为有多少个节点。

但是我们这里对于每一个节点 $v$ 不能以 $t_{v}$ 为下标，而是要以上文的 $t_{max}$ 为下标，于是要动态维护下标，在线段树合并之前，我们把每个以 $u'$ 为根点的线段树中所有 $t < t_{u'}$ 的点都移动到 $t_{u'}$ 的位置，我们需要知道 $t$ 在 $(-10^8, t_{u'})$ 的节点的个数以及它们的 $\sum val$ 即可，这个可以直接用线段树查，修改就是单点修改。

考虑样例的那棵树：

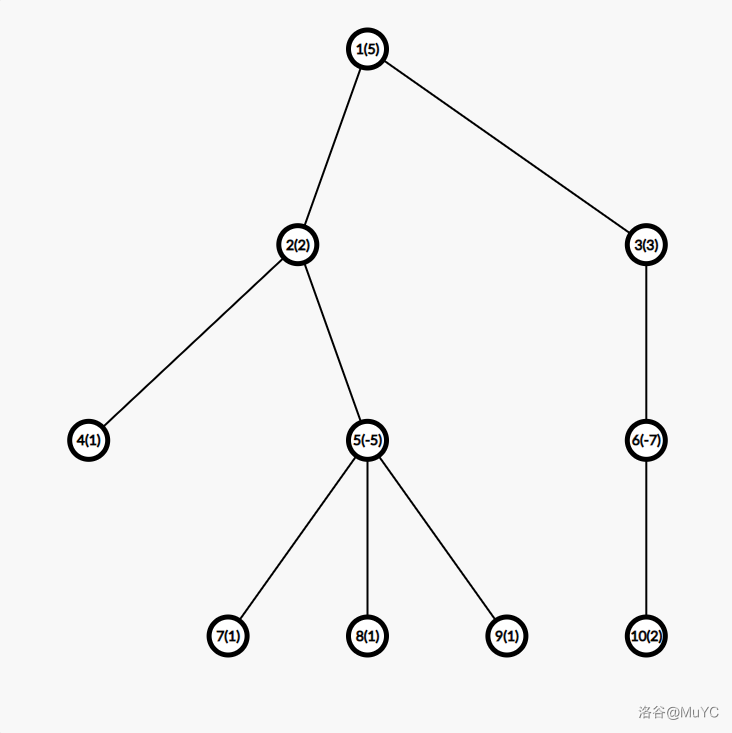
我们假设要求 $t_2$，那么我们现在知道：$t_{4} = -1,t_{5} = t_{7} = t_{8} = t_9 = 1$（$7,8,9$ 号点都被 $5$ 给覆盖了）。

那么假设二分到 $k = 1$ 的时候，那么就会是 $Sum = 1 \times 5 + 1 + 1 + 1 - 5 + 1 = 4$，显然大于 $-val[2]$，这个时候说明 $k = 1$ 是可以的。

当 $k = 0$ 的时候，$Sum = 0 \times 1 + 1 = 1$，也大于 $-val[2]$，可行。

$k = -1, Sum = -1 \times 1 + 1 = 0$，也大于 $-val[2]$，可行。

（上面的式子中 $Sum$ 的形式为：$Sum = k \times cnt + \sum val$）

那么 $k = -2$ 即为极小值，说明 $t_{2} = -2$。

于是我们可以对于每一个点 $u$ 求出 $t_{u}$。

现在我们能够求出 $t_{u}$ 后，就直接利用线段树查询当加上的权值为 $x$ 的时候所有节点的贡献为多少（与求 $t_{u}$ 的时候求 $Sum$ 是一样的做法）。

时空复杂度均为 $O(n \log n)$。

Code

可能人菜常数大，这份代码有一点卡常（）。

#include <bits/stdc++.h>
using namespace std;
#define Rep(i, l, r) for(int i = l ; i <= r ; i ++)
#define Lep(i, r, l) for(int i = r ; i >= l ; i --)

inline int read() {
    int x = 0, flag = 1;
    char ch = getchar();
    for( ; ch > '9' || ch < '0' ; ch = getchar()) if(ch == '-') flag = -1;
    for( ; ch >= '0' && ch <= '9' ; ch = getchar()) x = x * 10 + ch - '0';
    return x * flag;
}
const int MAXN = 1e6 + 50;
typedef long long LL;
int n, val[MAXN], tim[MAXN], siz[MAXN];
int rt[MAXN], pos[MAXN], cnt = 0, m;
LL Ans[MAXN], TSUM;
vector <int> E[MAXN];
struct SegmentTree1 {
    int ls, rs, siz; LL tsum;
} T[MAXN * 62];
struct Qs { 
    int tim, id; 
    bool operator <(const Qs& f) const { return tim < f.tim; }
} ;
vector <Qs> Q[MAXN];
bool cmp(int a, int b) { return tim[a] < tim[b]; }
void erase(int x) { T[x].ls = T[x].rs = T[x].siz = T[x].tsum = 0; }
int Get(int x, int P, int l, int r, int w, LL Sz, LL tsum) { // 线段树上二分求 t[x]
    if(l == r) return l - 1e8;
    int mid = (l + r) >> 1; LL SumL = mid - 1e8, sz = 0, t = 0;  //下面的所有 1e8 都是为了防止下标为负数
    for(int i = 0 ; i <= P ; i ++) {
        int u = pos[E[x][i]], ls = T[u].ls, p = mid - 1e8;
        if(mid - 1e8 < tim[E[x][i]]) continue;
        SumL += 1ll * p * T[ls].siz - T[ls].tsum;
        sz += T[ls].siz, t += T[ls].tsum;
    } SumL -= tsum, SumL += 1ll * (mid - 1e8) * Sz;
    if(SumL >= w) {
        Rep(i, 0, P) pos[E[x][i]] = T[pos[E[x][i]]].ls;
        return Get(x, P, l, mid, w, Sz, tsum);
    }
    Rep(i, 0, P) pos[E[x][i]] = T[pos[E[x][i]]].rs;
    return Get(x, P, mid + 1, r, w, sz + Sz, tsum + t);
}
int merge(int x, int y) { // 线段树合并
    if(!x || !y) return x | y;
    int cur = ++ cnt;
    T[cur].siz = T[x].siz + T[y].siz;
    T[cur].tsum = T[x].tsum + T[y].tsum;
    T[cur].ls = merge(T[x].ls, T[y].ls);
    T[cur].rs = merge(T[x].rs, T[y].rs);
    erase(x), erase(y); return cur;
}
void insert(int &x, int l, int r, int pos, int a, LL b) { // 修改某个点的权值
    if(!x) x = ++ cnt; int mid = (l + r) >> 1;
    T[x].siz += a, T[x].tsum += b;
    if(l == r) return ;
    if(pos + 1e8 <= mid) insert(T[x].ls, l, mid, pos, a, b);
    else insert(T[x].rs, mid + 1, r, pos, a, b);
    T[x].siz = T[T[x].ls].siz + T[T[x].rs].siz;
    T[x].tsum = T[T[x].ls].tsum + T[T[x].rs].tsum;
    return ;
}
int Cover(int &x, int l, int r, int pos) { //区间全部置 0
    int cur = x, Sz = 0;
    if(l == r) { TSUM += T[x].tsum, Sz = T[cur].siz, erase(x), x = 0; return Sz; }
    int mid = (l + r) >> 1;
    if(pos + 1e8 <= mid) Sz = Cover(T[x].ls, l, mid, pos);
    else {
        Sz += T[T[x].ls].siz, TSUM += T[T[x].ls].tsum,
        erase(T[x].ls), T[x].ls = 0, 
        Sz += Cover(T[x].rs, mid + 1, r, pos);
    }
    T[x].siz = T[T[x].ls].siz + T[T[x].rs].siz;
    T[x].tsum = T[T[x].ls].tsum + T[T[x].rs].tsum;
    return Sz;
}
LL Find(int x, int l, int r, int pos) {
    if(!x) return 0;
    if(l == r) return 1ll * pos * T[x].siz - T[x].tsum;
    int mid = (l + r) >> 1;
    if(pos + 1e8 <= mid) return Find(T[x].ls, l, mid, pos);
    return Find(T[x].rs, mid + 1, r, pos) +  1ll * pos * T[T[x].ls].siz - T[T[x].ls].tsum;
}
void dfs1(int x) {
    int Siz = E[x].size() - 1, now = 0;
    Rep(i, 0, Siz) {
        dfs1(E[x][i]);
        pos[E[x][i]] = rt[E[x][i]]; TSUM = 0;
        int fs = Cover(rt[E[x][i]], 0, 2e8, tim[E[x][i]] - 1);
        insert(rt[E[x][i]], 0, 2e8, tim[E[x][i]], fs, TSUM);
    }
    tim[x] = Get(x, Siz, 0, 2e8, -val[x], 0, 0);
    sort(E[x].begin(), E[x].end(), cmp);

    while(now != Q[x].size()) {
        int Tim = Q[x][now].tim, Id = Q[x][now].id;
        if(E[x].size() == 0) { Ans[Id] = val[x] + Tim; now ++; continue; }
        if(Tim < tim[E[x][0]]) { Ans[Id] = val[x] + Tim; now ++; continue; }
        break;
    }

    Rep(i, 0, Siz) {
        rt[x] = merge(rt[x], rt[E[x][i]]);
        if(now == Q[x].size()) continue;
        int Tim = Q[x][now].tim, Id = Q[x][now].id, f;
        while(Tim >= tim[E[x][i]] && now < Q[x].size()) {
            if(i != Siz) if(Tim >= tim[E[x][i + 1]]) break;
            Ans[Id] = Find(rt[x], 0, 2e8, Tim) + Tim + val[x];
            now ++; if(now == Q[x].size()) break;
            Tim = Q[x][now].tim, Id = Q[x][now].id;
        }
    }
    insert(rt[x], 0, 2e8, tim[x], 1, -val[x]);
    return ;
}
inline void Write(LL x, char c) {
    LL Putout[35], Numbercnt = 0;
    if(x < 0) putchar('-'), x = -x;
    if(!x) { putchar('0'), putchar(c); return ; }
    while(x) Putout[++ Numbercnt] = x % 10, x /= 10;
    for(int i = Numbercnt ; i >= 1 ; i --) putchar(Putout[i] + '0');
    if(Numbercnt == 0) putchar('0'); putchar(c);
    return ;
}

int main() {
    n = read(), m = read();
    Rep(i, 2, n) E[read()].push_back(i);
    Rep(i, 1, n) val[i] = read();
    Rep(i, 1, m)  {
        int u = read(), x = read();
        Q[u].push_back((Qs) { x, i } );
    } 
    Rep(i, 1, n) sort(Q[i].begin(), Q[i].end()); dfs1(1);
    Rep(i, 1, m) Write(Ans[i], ' '), putchar('\n');
    return 0;
}
// time limit: 3 s
// memory limit: 2.00 GB
// Author: MuYC