自动搬运

查看原文

来自洛谷，原作者为

	persimmon2008 **

搬运于2025-08-24 22:33:57，当前版本为作者最后更新于2021-10-01 16:33:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

这不就是一个最最最简单的找规律吗!?

思路

我们先来看一下这两种特殊情况：

case1:

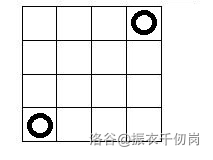
即 $|a-c|=|b-d|$

因为相邻两边方向不相同，所以有最小代价如下图：

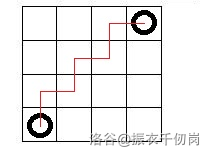
即最小代价 $=|a-c| + |b-d|$

case2:

即 $a==c \parallel b==d$

相邻两边方向不相同,只能以 $→↑→↓→↑→↓$ 的方向移动，如下图：

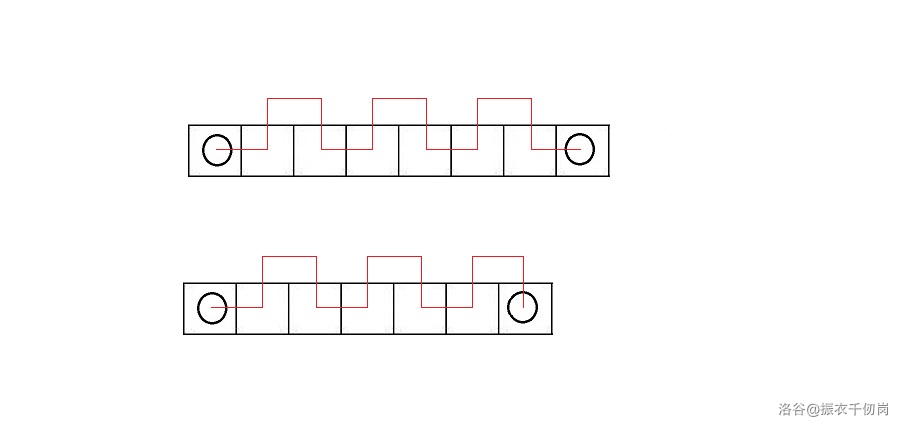
此时的最小距离分为两类：(假设b $=$ d)

直线距离为偶数时：距离为 $|a-c| \div 2 \ast 4$

直线距离为奇数时：距离为 $|a-c| \div 2 \ast 4 + 1$

$|a-c| \div 2 \ast 4$ 可以约成 $|a-c| \ast 2$

而在$|a-c| \div 2$中，向下取整后会把多出的一步加在后面，便不能约了。

Code

容易想到，任何两点都可以由上述两种情况构成的，如:

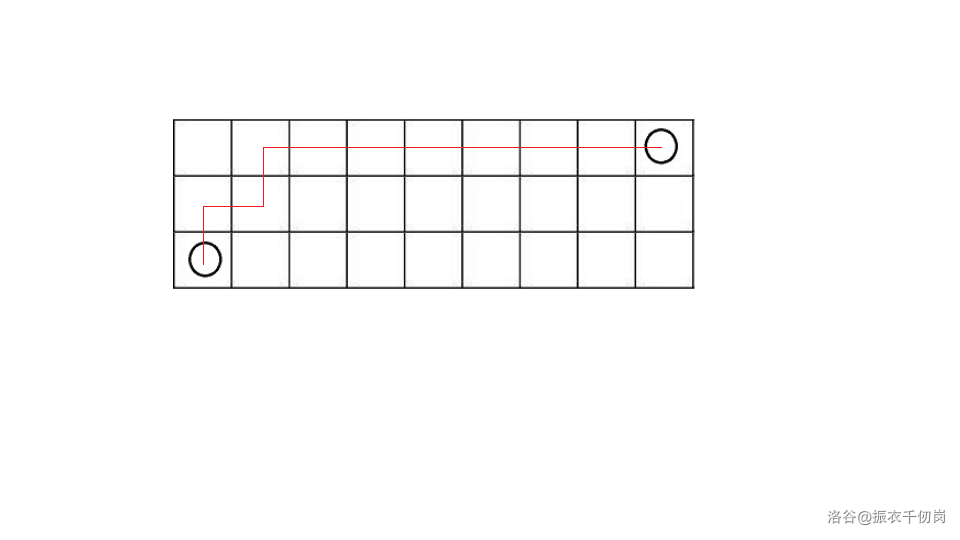
所以，我写出了如下代码，仅供参考。

#include<iostream>
#include<cstdio>
#include<cmath>
#define int long long
using namespace std;
inline int read() {
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') {
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
		s=(s<<1)+(s<<3)+(ch^48),ch=getchar();
	return s*w;
}
inline void write(int x) {
	if(x>9)
		write(x/10);
	putchar(x%10+'0');
}
signed main() {
	int n=read();
	while(n--){
		int a=read(),b=read();
		int c=read(),d=read();
		int x=abs(a-c),y=abs(b-d);
		if(x>y)swap(x,y);
		int ans=0;
		ans+=x*2;
		if(abs(x-y)%2)ans+=abs(x-y)/2*4+1;
		else ans+=abs(x-y)*2;
		write(ans);
		putchar('\n');
	}
}

完结撒花，不点个赞再走吗。