自动搬运

查看原文

来自洛谷，原作者为

	Avocadooo ZEST FOR LIFE

搬运于2025-08-24 22:33:46，当前版本为作者最后更新于2021-09-16 13:12:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

正经教学

1.题目类型判断

有两个帅哥人，他们都需要运用最优策略以获得胜利。

每个人可以在一回合内摘叶子节点。

很明显，这是一道关于树的叶子节点的博弈论题目。

2.基本思路

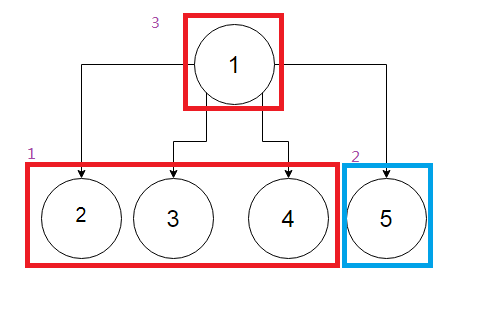
结论1：若当前存在一棵树 $S$，那么在树 $S$ 上的任意一非叶子节点上添加一个子节点，生成一棵新的树 $S'$，那么 $S'$ 对于先手一定为必胜态。

证明：

(1) 如果开始是必胜态。因为我们是通过一个非叶子节点添加点 Extra ，可知 Extra 也是一个叶子节点，先手根据必胜态所取点加上 Extra ，留给对方的同样是必败态。

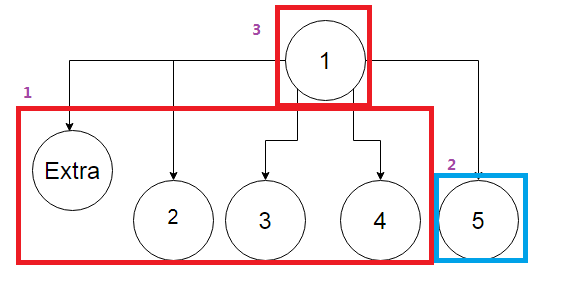
(2) 如果开始是必败态，利用非叶子节点增加一个点 Extra ，且第一次直接选择 Extra，那么必败态就送给对面了对面很喜欢。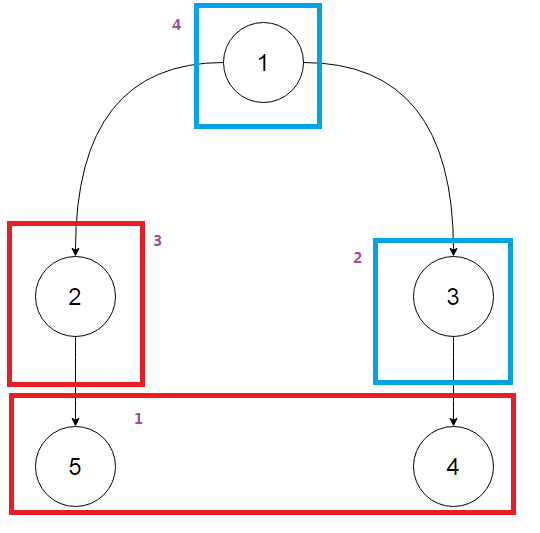

结论2：若树 $U$ 存在任意一个叶子节点不是“孤独的叶子”（便于理解,自己取的名字 （作者觉得这个名字很美妙）） (即该叶子节点的父亲节点的子节点为叶子节点的数量 $\geq 2$ ) ，则树 $U$ 对于先手必胜。

证明：

题目条件 $n \geq 1$ 可知树 $S \neq \varnothing$，所以 $S$ 中至少存在一个节点为叶子节点；

我们把非“孤独的叶子”的一个节点的父亲的其它子节点的其中一个看作结论1证明中的 Extra ，无论去掉 Extra 后的树 $U'$ 为必胜态还是必败态；

根据结论1，加上了 Extra 的树 $U$ 一定为必胜态。欧耶！！！

这是一个例子：

原始树是这个样子；

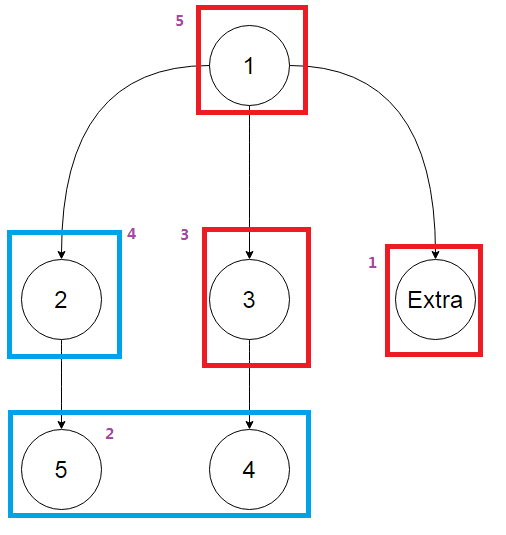
我们把点5看为 Extra ；

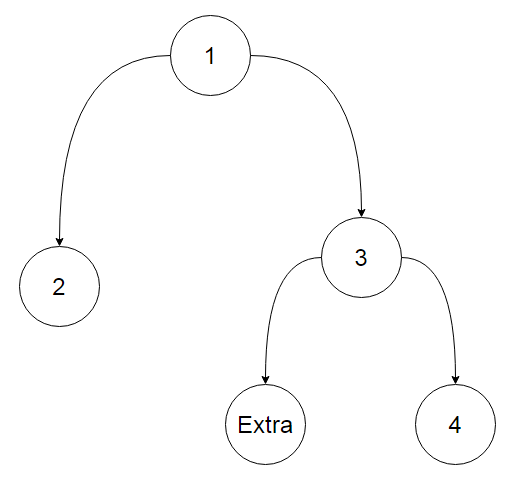
此时不管下图是否为必胜或者必败，加上 Extra 的树一定是必胜态（结论1）。

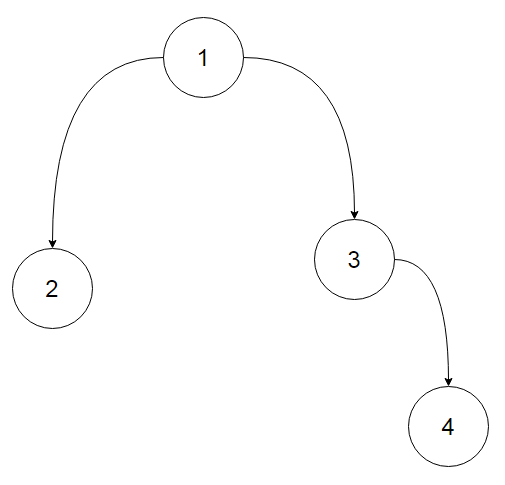
(2) 若不存在一个叶子结点父亲有多于一个儿子，考虑每个叶子（含）到深度最大的儿子个数多于1的祖先（不含）之间的点数。若所有的这些数都是偶数，那么后手必胜，因为后手可以模仿先手直到存在一个叶子结点父亲有多于一个儿子（也就是某个叶子到深度最大的儿子个数多于1的祖先只剩1的距离了），从而达到必胜态。否则先手必胜，因为先手可以一步转换为后手必胜状态。

（这位作者很懒，什么也没有画）

3.std代码

#include<bits/stdc++.h>
using namespace std;
int fa[1000005];
vector<int> leaves;
int du[1000005],Ks[1000005];
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		int n,x;
		scanf("%d",&n);
		leaves.clear();
		for(int i=1;i<=n;i++)
		{
			Ks[i]=du[i]=0;
		}
		for(int i=2;i<=n;i++)
		{
			scanf("%d",&x);
			fa[i]=x;
			du[x]++;
			Ks[x]++;
		}
		for(int i=1;i<=n;i++)
			if(du[i]==0) leaves.push_back(i);
		bool flag=0;
		for(vector<int>::iterator it=leaves.begin();it!=leaves.end();it++)
		{
			int v=*it;
			int father=fa[v];
			if(Ks[father]>=2)
			{
				flag=1;
				break;
			}
			int cnt=1;
			while(Ks[fa[v]]==1)
			{
				cnt++;
				v=fa[v];
			}
			if(cnt&1)
			{
				flag=1;
				break;
			}
		}
		if(flag) printf("1\n");
		else printf("0\n");
	}
	return 0;
}