自动搬运

查看原文

来自洛谷，原作者为

	Binary_Lee Away From OI

搬运于2025-08-24 22:33:44，当前版本为作者最后更新于2022-09-06 19:22:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题面传送门

好题。

主要思路和另一位巨佬差不多，详细讲一下判断的部分。

解决思路：

首先考虑本题与拓扑排序有和关系。可以想到，某些棍子的先后移动顺序是有限制的。比如：

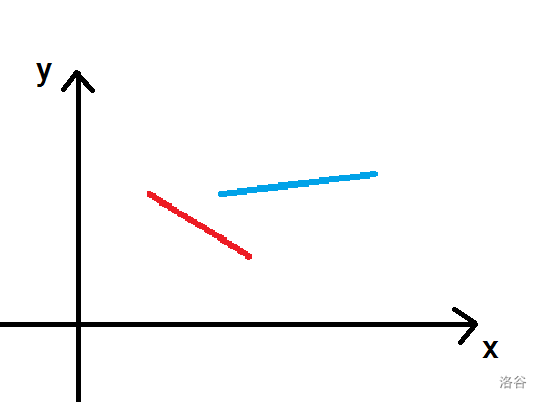
这里红色的必须比蓝色的先移动，因为它们在 $x$ 轴的投影有重叠，蓝色在上，会被红色卡住。

所以，棍子两两之间可能存在限制关系，这就符合拓扑排序的条件了。考虑根据每一对限制关系建边。若 $u$ 必须比 $v$ 先移动，就从 $u$ 向 $v$ 连边，这样就转化为求拓扑序问题了。

其次，也是较麻烦的一部分，就是如何根据两线段的坐标判断其移动先后限制。

为了方便，在读入时判断并交换好，用 $x1,y1$ 表示左边端点，$x2,y2$ 表示左边端点。

$\text {check}$ 函数，分以下几种情况讨论：

1. 没有限制关系，返回 $0$。
2. $u$ 比 $v$ 要先移动，返回 $-1$。
3. $v$ 比 $u$ 要先移动，返回 $1$。

为了方便，设 $u$ 为靠左的线段，若不是，在开始判断前将交换一下，并需要把 $op$（返回值）取反。

首先看 $op=0$，即两线段在 $x$ 轴上投影不重合：

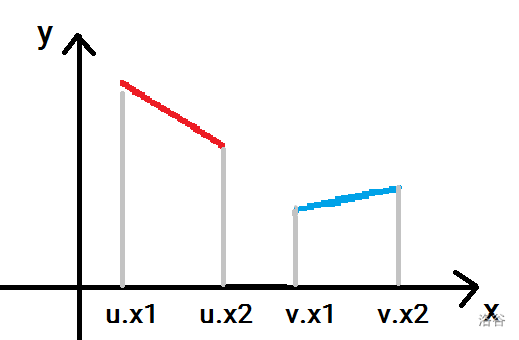
肉眼可见，$u.x2<v.x1$，注意等号不可以取到（照提交意思来看...）。

然后看一般情况。多画几个图，可以发现，只需要比较 $u$ 上 $x=v.x1$ 时 $u.y'$ 的值与 $v.y1$ 的大小 即可（或 $v$ 上 $x=u.x2$ 时 $v.y'$ 的值与 $u.y2$ 的大小）。在下的先移，在上的后移。

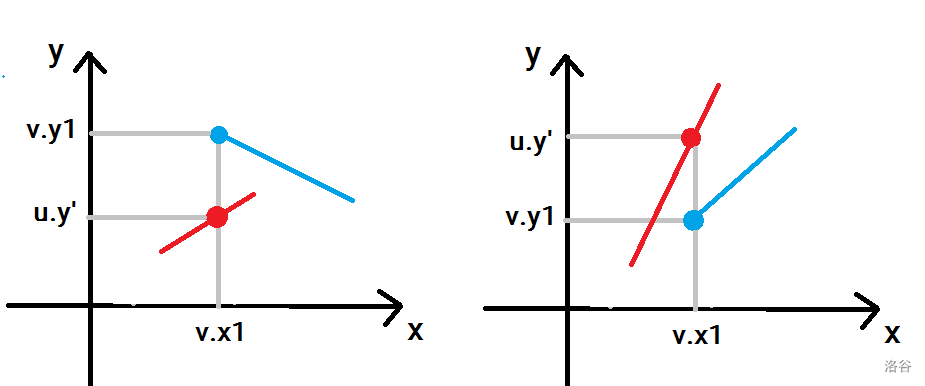
至于如何求函数值。。上过初中数学都会。具体可以看程序，变量名都遵从 $y=kx+b$ 的基本形式了。

然鹅，这样写获得了 $95$ 分的高分。哪里出问题了？

还有一种比较坑的情况，就是 $u$ 是竖直的！

这时候函数 $u$ 的 $k$ 是无限大的，不是一次函数，无法求出值。所以需要特判，算出 $x=u.x1$ 时 $v$ 的函数值再比较。

Code：

#include<bits/stdc++.h>
using namespace std;
int n,m,in[5005];
struct node{
	int x1,x2,y1,y2;
}b[5005];
vector<int> a[5005];
queue<int> q;
int check(node u,node v){ //0:无关，-1:先移u，1:先移v 
	int op=1;		
	if(u.x1>v.x1) swap(u,v),op=-op;	
	if(u.x2<v.x1) return 0; 
	double K,B,tmp;
	if(!(u.x2-u.x1)){
		K=1.0*(v.y2-v.y1)/(v.x2-v.x1);
		B=(double)v.y1-K*v.x1;
		tmp=K*u.x1+B;
		if(u.y1>tmp) return op;
		return -op;
	}
	K=1.0*(u.y2-u.y1)/(u.x2-u.x1);
	B=(double)u.y1-K*u.x1;
	tmp=K*v.x1+B;   //求函数
	if(tmp>v.y1) return op;
	return -op;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d%d",&b[i].x1,&b[i].y1,&b[i].x2,&b[i].y2);
		if(b[i].x1>b[i].x2) swap(b[i].x1,b[i].x2),swap(b[i].y1,b[i].y2);
	}
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			int op=check(b[i],b[j]);
			if(op==-1) a[i].push_back(j),in[j]++; 
			if(op==1) a[j].push_back(i),in[i]++;   //连边
		}
	}
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i),printf("%d ",i);
	while(q.size()){        //拓扑
		int k=q.front();
		q.pop();
		for(int i=0;i<a[k].size();i++){
			int tmp=a[k][i];
			in[tmp]--;
			if(!in[tmp]) q.push(tmp),printf("%d ",tmp);
		}
	}
	return 0;
}