1 条题解
-
0
自动搬运
来自洛谷,原作者为

Rainbow_qwq
**搬运于
2025-08-24 22:33:29,当前版本为作者最后更新于2022-01-21 23:48:33,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
bfs 序会把图分成若干层,考虑 DP 不停的加一层,有一个限制:原有的边不能有从第 层到第 层的;代价则是第 层中没有向第 层有边的。
可以设 表示分 为一层,转移枚举 ,可以得到 做法。
但是最终二维的做法还是不太行,需要再挖掘一下转移的性质。
设 表示前 个分成若干段的代价最小值,考虑从 ,发现如下的 是不能转移的:
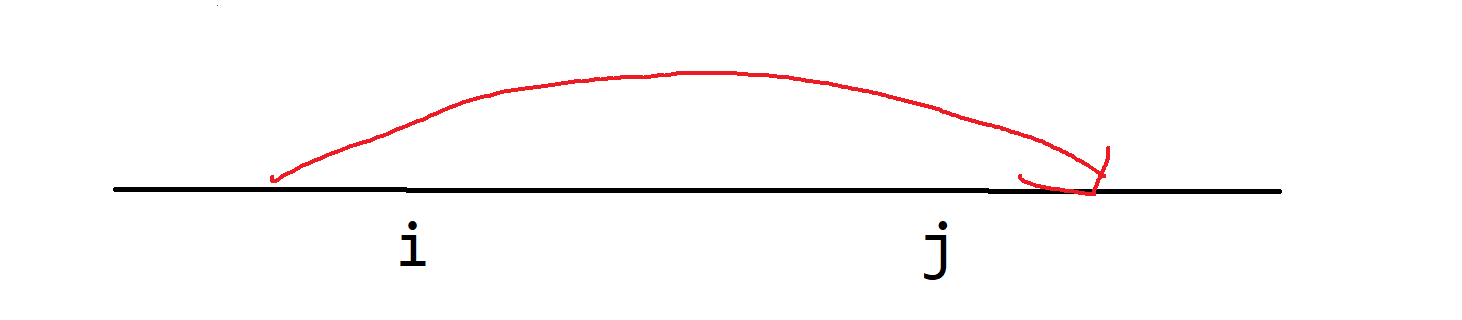
于是我们发现能转移的 是一段后缀。设 为 中 的最大值, 需要 。并且在 的部分, 每增大 1 代价就增大 1,代价是一段连续的数。
于是推一下就可以简单 DP 了,可以只向 能到的最小地方转移,后面 。
#include<bits/stdc++.h> #define For(i,a,b) for(register int i=(a);i<=(b);++i) #define Rep(i,a,b) for(register int i=(a);i>=(b);--i) //#define int long long using namespace std; inline int read() { char c=getchar();int x=0;bool f=0; for(;!isdigit(c);c=getchar())f^=!(c^45); for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48); if(f)x=-x;return x; } #define fi first #define se second #define pb push_back #define mkp make_pair typedef pair<int,int>pii; typedef vector<int>vi; #define maxn 200005 #define inf 0x3f3f3f3f bool vis[maxn]; int n,m,f[maxn],sum,mn[maxn],mx[maxn],g[maxn]; vi e[maxn]; void addin(int x){sum+=(!vis[x]),vis[x]=1;} signed main() { n=read(),m=read(); For(i,1,n)mn[i]=n+1; For(i,1,m){ int u=read(),v=read(); mn[u]=min(mn[u],v); mn[v]=min(mn[v],u); mx[u]=max(mx[u],v); mx[v]=max(mx[v],u); e[min(u,v)].pb(max(u,v)); } For(i,1,n)mx[i]=max(mx[i],mx[i-1]); memset(f,63,sizeof f); // For(j,2,n){ // int sum=0,p=j-1; // For(i,max(j,mx[j-1]),n){ // while(p<i) ++p,sum+=(mn[p]>j-1); // f[i]=min(f[i],f[j-1]+sum); // } // } For(j,1,n-1){ f[j]=min(f[j],f[j-1]+1); int nowf=(j==1?0:f[j]); addin(j); for(auto v:e[j])addin(v); // mx[j] int to=max(mx[j],j+1); f[to]=min(f[to],nowf+to-sum); } cout<<f[n]; return 0; }
- 1
信息
- ID
- 7163
- 时间
- 1000ms
- 内存
- 128MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
