1 条题解
-
0
自动搬运
来自洛谷,原作者为

hensier
**搬运于
2025-08-24 22:33:15,当前版本为作者最后更新于2021-08-17 18:45:37,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题目中出现了至多和最小等字眼,因此很有可能需要使用二分答案。
怎么进行二分呢?我们对 进行二分并检验当前 值是否符合题意。不难发现,如果一个点到原点的距离不超过 ,那么这个点一定符合(所有正比例函数都经过原点)。因此我们只需考虑 的点。
由于到一个点距离不超过 的集合就是以该点为圆心, 为半径的圆内,因此我们只需要求出该圆过原点的两条切线的斜率即可。显然在这两条直线 和 之间(不一定是斜率之间)的所有直线都是符合题意的:
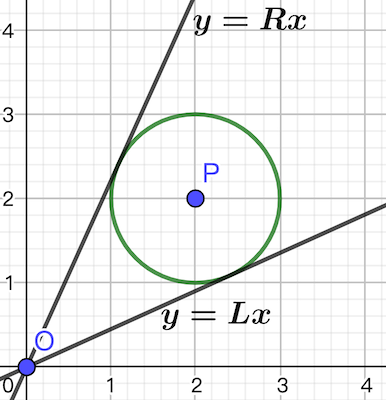
我们只需要找到这 个点对应的 值,将这些点的 抽象成 条线段,就可以把问题转化成用最少的点覆盖所有线段的经典贪心问题,并以最少的点数是否小于等于 作为二分答案的判断条件。
那么最关键的就是如何求解每个点的 。这里有三种方法:
Solution 1 二分套二分
为什么题目要提供点和直线的距离公式呢?实际上,根据之前插图的演示,不难发现直线与点的距离满足一定的单调性。我们可以利用这个性质再一次二分,得到 的值。
对于斜率等于 的情形,我们可以直接在二分前进行处理,例如将其修改成一个足够大的数。
该做法的时间复杂度为 ( 为二分区间大小):
#include<bits/stdc++.h> using namespace std; int n,k; long double l,r=100000,ans; // 将二分区间右端点 r 调成一个较大的值 struct point { long double x,y; }p[25001]; struct interval { long double L,R; bool operator<(const interval &x)const { return R<x.R; } }a[25001]; bool check_dis(int x,int y,long double k,long double d) { long double dis=fabs(y-k*x)/sqrt(k*k+1); return dis<=d; } interval get(point p,long double d) { if(!p.x)return (interval){-p.y/d,p.y/d}; // 特判 x 为 0 的特例 interval ans; long double l=0,r=p.y/p.x; // 第一条切线一定在点 P 的下方 while(l<=r) { long double mid=(l+r)*0.5; if(check_dis(p.x,p.y,mid,d)) { r=mid-0.00000001; // 第二个二分需要很高的精度,否则无法通过 ans.L=mid; } else l=mid+0.00000001; } l=p.y/p.x,r=100000; // 第二条切线一定在点 P 的上方 while(l<=r) { long double mid=(l+r)*0.5; if(check_dis(p.x,p.y,mid,d)) { l=mid+0.00000001; ans.R=mid; } else r=mid-0.00000001; } return ans; } bool check(long double d) { int cnt=0; for(int i=1;i<=n;++i) { if(sqrt(p[i].x*p[i].x+p[i].y*p[i].y)<=d)continue; // 不需要考虑到原点距离已经不超过 d 的点 a[++cnt]=get(p[i],d); // 二分得到斜率区间 } sort(a+1,a+cnt+1); // 排序并用贪心求解 int tot=0; long double tmp=0; for(int i=1;i<=cnt;++i) { if(tmp<=a[i].L) { tmp=a[i].R; if(++tot>k)return false; // 一旦需要的直线数量超过 k 就说明不可行 } } return true; } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y); while(l<=r) { long double mid=(l+r)*0.5; if(check(mid)) { r=mid-0.0001; // 由于只需要保留两位小数,因此精度可以稍低 ans=mid; } else l=mid+0.0001; } printf("%.2Lf",ans); return 0; }Solution 2 二分+导角
我们可以通过角和斜率之间的转化求解。
考虑下图的情形(两条直线斜率都非负):
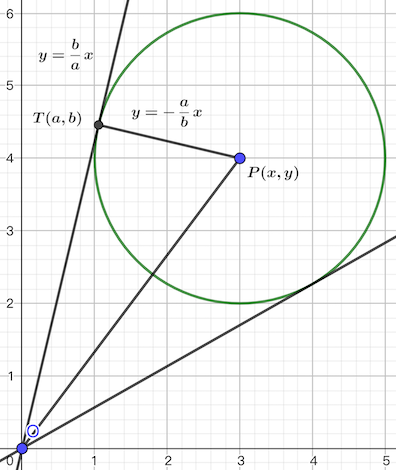
我们可以用反正切函数求出 与 轴正方向的夹角 ,用反正弦函数求出 。由于两条切线与 之间的夹角相等,因此两条切线与 轴正半轴的夹角为 。
我们还需考虑下面两种情形:
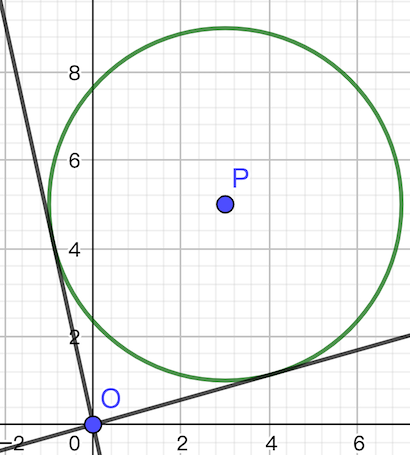
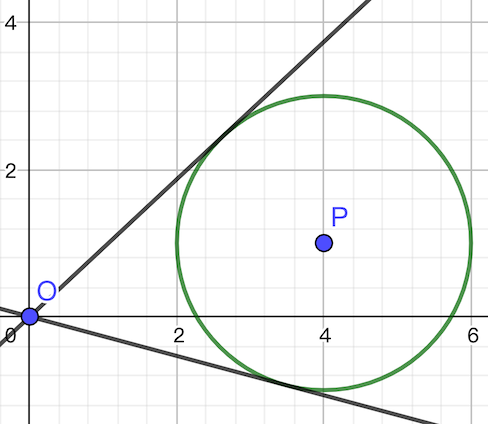
这种情形下切线斜率一正一负,而这此时直接把负的当左端点、正的当右端点显然是错误的(有一个跨 的过程)。又因为题中没有负坐标,因此只需要保留正斜率。那么:
- 在第一种情形中,符合题意的所有斜率的最小值为其中的正斜率,最大值为 。
- 在第二种情形中,最小值为 ,最大值为其中的正斜率。
考虑当前的点属于哪一种情形:
- 当切点位于第二象限时(此时 ),属于第一种。
- 当切点位于第四象限时(此时 ),属于第二种。
那么,为什么二分套二分的方法不需要对此进行考虑呢?这是因为,我们可以在求解 时将二分下界设为 ,这样就避免了需要讨论负斜率的情况。
该做法的时间复杂度为 :
#include<bits/stdc++.h> using namespace std; const double rt=acos(-1)*0.5; // 预处理 90° 弧度制下的值,即 0.5π int n,k; long double l,r=100000,ans; struct point { long double x,y; }p[25001]; struct interval { long double L,R; bool operator<(const interval &x)const { return R<x.R; } }a[25001]; bool check(long double d) { int cnt=0; for(int i=1;i<=n;++i) { long double x=p[i].x,y=p[i].y; if(x*x+y*y<=d*d)continue; ++cnt; long double alpha,beta; alpha=atan(y/x); // 求出 OP 与 x 轴的夹角 if(!x)alpha=rt; // 如果 x=0 则与 x 轴的夹角为 90° beta=asin(d/sqrt(x*x+y*y)); // 求出切线与 OP 连线的夹角 a[cnt].L=tan(alpha-beta),a[cnt].R=tan(alpha+beta); if(a[cnt].L>a[cnt].R)swap(a[cnt].L,a[cnt].R); if(a[cnt].L<0) { if(alpha+beta>rt) { a[cnt].L=a[cnt].R; a[cnt].R=1e18; } else a[cnt].L=0; } } sort(a+1,a+cnt+1); int tot=0; long double tmp=0; for(int i=1;i<=cnt;++i) { if(tmp<=a[i].L) { tmp=a[i].R; if(++tot>k)return false; } } return true; } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y); while(l<=r) { long double mid=(l+r)*0.5; if(check(mid)) { r=mid-0.0001; ans=mid; } else l=mid+0.0001; } printf("%.2Lf",ans); return 0; }Solution 3 二分+导边
借助之前的示意图:

不妨设 的坐标为 ,则 的斜率为 , 的斜率为 。把 和 代入得 。化简得 。
又因为 ,因此有 。化简得 。
由于 为常数,因此可设 。
因此
$$\begin{cases} a^2+b^2=ax+by & (1) \cr a^2+b^2-2ax-2by=c & (2) \cr \end{cases}$$把 代入 得
因此我们可以将 用 进行表示(仅在 时成立):
再代回 得:
$$a_{1,2}=\dfrac{-2cx±\sqrt{4c^2x^2-4(x^2+y^2)(c^2+cy^2)}}{2(x^2+y^2)} $$$$=\dfrac{-cx±\sqrt{c^2x^2-(x^2+y^2)(c^2+cy^2)}}{x^2+y^2} $$最后求出 即可得到两条直线的斜率。
特判 的情形:
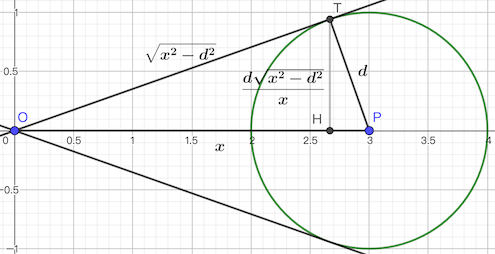
此时 ,,。
作 于 ,则 。因此 ,即 。然后再在 中用一次勾股定理即可求出 。最后斜率即为 。
由于 ,因此较下方的切线的斜率必然为负。之前提到了本题无需考虑负斜率,因此取斜率的最小值为 ,最大值为 即可。
的情形不需单独考虑,因为其斜率的范围显然为 ,适用于一般情况。
与导角的方法类似,我们仍需考虑这两种情形:


考虑每个点属于哪一种情形:
- 当负斜率的切点位于 轴上方时,第一种情形成立。
- 当负斜率的切点位于 轴下方时,第二种情形成立。
相比于导角的做法,该做法时间复杂度仍为 ,但不涉及反三角函数的使用,因此常数较小:
#include<bits/stdc++.h> using namespace std; int n,k; long double l,r=100000,ans; struct point { long double x,y; }p[25001]; struct interval { long double L,R; bool operator<(const interval &x)const { return R<x.R; } }a[25001]; bool check(long double d) { int cnt=0; for(int i=1;i<=n;++i) { long double x=p[i].x,y=p[i].y; if(x*x+y*y<=d*d)continue; ++cnt; if(!y) // 考虑 y=0 的情况 { a[cnt].L=0; long double b1=d*sqrt(x*x-d*d)/x; long double a1=sqrt(x*x-d*d-b1*b1); a[cnt].R=b1/a1; } else { long double c=d*d-x*x-y*y,delta=-c*(x*x+y*y+c); long double a1=(-c*x+y*sqrt(delta))/(x*x+y*y); long double a2=(-c*x-y*sqrt(delta))/(x*x+y*y); long double b1=(-c-a1*x)/y,b2=(-c-a2*x)/y; a[cnt].L=b1/a1,a[cnt].R=b2/a2; if(a[cnt].L>a[cnt].R) { swap(a[cnt].L,a[cnt].R); swap(a1,a2); swap(b1,b2); // 一定要注意连同 a1,a2,b1,b2 同时 swap,否则会影响下面对答案的修正 } if(a[cnt].L<0) // 一正一负的情形下,负的必然存储在 L 中 { if(b1>0) { a[cnt].L=a[cnt].R; a[cnt].R=1e18; // 将右端点赋为极大值 } else a[cnt].L=0; // 否则将左端点由负改为 0 即可 } } } sort(a+1,a+cnt+1); int tot=0; long double tmp=0; for(int i=1;i<=cnt;++i) { if(tmp<=a[i].L) { tmp=a[i].R; if(++tot>k)return false; } } return true; } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y); while(l<=r) { long double mid=(l+r)*0.5; if(check(mid)) { r=mid-0.0001; ans=mid; } else l=mid+0.0001; } printf("%.2Lf",ans); return 0; }
- 1
信息
- ID
- 7121
- 时间
- 1000ms
- 内存
- 128MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
