自动搬运

查看原文

来自洛谷，原作者为

	佬头 {暴力出奇迹，骗分过样例，暴搜挂着机，打表出省一}ด้้้้้็้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้(已退役)

搬运于2025-08-24 22:32:46，当前版本为作者最后更新于2023-11-15 16:26:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Description

有 $k$ 种颜色和 $n$ 个图像，图像编号从 $1$ 到 $n$。给定 $n$ 个 $f_i$ 并按照如下方法用 $k$ 种颜色涂色：

• 若 $f_i\ne i$，则图像 $i$ 不能与图像 $f_i$ 的颜色相同。
• 若 $f_i=i$，图像 $f_i$ 可以涂成任何颜色。

求出可能的涂色总方案数，答案对 $\bm{10^9+7}$ 取模。

Solution

由 $i$ 向 $f_i$ 建边，那么每个点就仅有一条出边，如果从一个点 $i$ 不断沿着 $f_i$ 走，总会陷入一个环中（包括 $f_i=i$），因此不难想到它会是一棵内向基环树，整幅图就是一张内向基环森林。类似于：

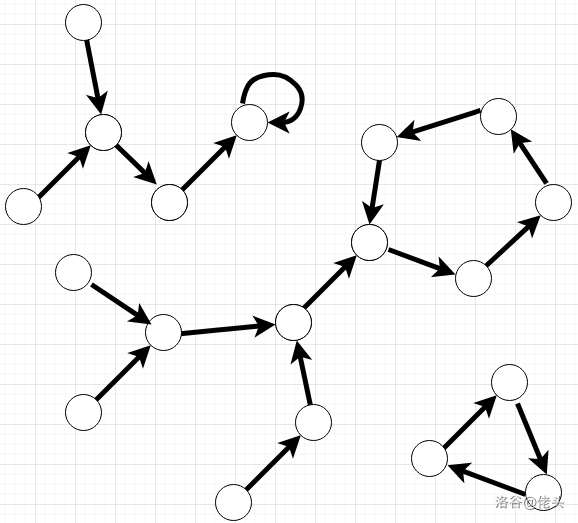
内向基环树可以形象地理解为一个环上长了若干棵树，当然也存在某个没长树的环，那就把环和树分开来考虑（显然两种情况的限制是不一样的）：

• 对于一棵树而言，如果其根结点的涂色固定，则其儿子结点的涂色就都是 $(k-1)$ 种。同理：对于所有树上的非叶子结点，他们的儿子结点的涂色方案数也都为 $(k-1)$ 种（仅保证每个结点与其父结点的涂色不同即可）。那么一棵大小为 $size$ 的树对答案的贡献就是 $ans\gets ans\times (k-1)^{size-1}$（根结点的涂色固定了，因此减一）。
• 接下来就是环。显然每个环除结点数以外都是相类似的，考虑 dp：设 $dp_i$ 表示有 $i$ 个结点的环的方案数：

  • 当 $1\le i\le3$ 的情况是显然的（每个点都互不相同）：

    • $dp_1=k$；
    • $dp_2=k\times(k-1)$；
    • $dp_3=k\times(k-1)\times(k-2)$。

  • 当 $i\gt3$ 时：

    • 从 $i-1$ 的环里插入一个结点 $A$，此时与 $A$ 相连的两个结点互不相同，则 $A$ 的涂色方案就有 $(k-2)$ 种。
    • 把 $i-2$ 的环里的一个结点拆成两个完全相同的结点，同时在中间插入结点 $A$，此时与 $A$ 相连的两个结点完全相同，则 $A$ 的涂色方案就有 $(k-1)$ 种。

    则递推式就是 $dp_i=dp_{i-1}\times\left(k-2\right)+dp_{i-2}\times\left(k-1\right)~(i\gt 3)$。

    这个显然可以预处理掉，最后我们只需要把每个环的大小 $size$ 求出来再更新答案即可 $ans\gets ans\times dp_{size}$。（$i\gt3$ 是因为 $i=1$ 拆成的两个完全相同的结点相邻）

最后思考如何把树和环分开来。就用拓扑排序吧，把环以外的结点全部先计算掉，那么剩下的肯定都是单独的环，就很方便处理了。（我一开始还想用 tarjan 缩点来着，但是好像不用这么麻烦）

时间复杂度 $\mathcal O(n)$。

Code

#include <iostream>
using namespace std;
const int N = 1000006, mod = 1000000007;
int n, k, dp[N], f[N], out[N], ans = 1, q[N], back;
bool vis[N];
int read(){
	int x = 0;
	char a = getchar();
	while(a < '0' || '9' < a) a = getchar();
	while('0' <= a && a <= '9') x = (x << 1) + (x << 3) + (a ^ 48), a = getchar();
	return x;
}
void write(int x){
	if(x > 9) write(x / 10);
	putchar(x % 10 | 48);
}
int main(){
	n = read(), k = read();
	dp[1] = k;
	dp[2] = (long long)k * (k - 1) % mod;
	dp[3] = (long long)dp[2] * (k - 2) % mod;
	for(int i = 4; i <= n; ++ i) dp[i] = (long long)dp[i - 1] * (k - 2) % mod + (long long)dp[i - 2] * (k - 1) % mod;
	for(int i = 1; i <= n; ++ i) ++ out[f[i] = read()];
	for(int i = 1; i <= n; ++ i) if(!out[i]) q[++ back] = i;
	for(int front = 1; front <= back; ++ front){
		vis[q[front]] = 1;
		ans = (long long)ans * (k - 1) % mod;
		if(!-- out[f[q[front]]]) q[++ back] = f[q[front]];
	}
	for(int i = 1, cnt, x; i <= n; ++ i)
		if(!vis[i]){
			for(cnt = 0, x = i; !vis[x]; x = f[x]) vis[x] = 1, ++ cnt;
			ans = (long long)ans * dp[cnt] % mod;
		}
	write(ans);
	return 0;
}

Strengthen

P2607 [ZJOI2008] 骑士