1 条题解
-
0
自动搬运
来自洛谷,原作者为

ChengJY_
AFOed搬运于
2025-08-24 22:32:43,当前版本为作者最后更新于2021-10-05 21:27:26,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题目大意
给定一棵初始权值已知的树,每次操作:
- 对某个节点子树上的所有节点加上 。
- 查询某个节点的权值。
具体思路
-
1.暴力(112 pts)
对于每次修改操作,我们把修改值储存下来,然后每次询问操作我们历遍所求点的祖先,计算总和。
这看起来是 的正解,但是这仅限于这棵树是平衡的时候。在退化成链的极限条件下会被卡到 ,在 的数据范围下会T掉。
核心代码:
int a=read(); int x=tree[a].fa,w=tree[a].num; while(1){ if(x==0) break; w+=tag[x]; x=tree[x].fa; } printf("%d\n",w); -
2.正解(树状数组)(140 pts)
我们观察两个操作:
- 修改树上的一段区间。
- 求树上单点的值。
这不就是树状数组吗!
我们可以将树转化为一个差分数组,然后就是树状数组的模板了。
这题并不是完全意义上的树上差分,但是我们可以用类似于树剖的方法做。
这是样例二的树:
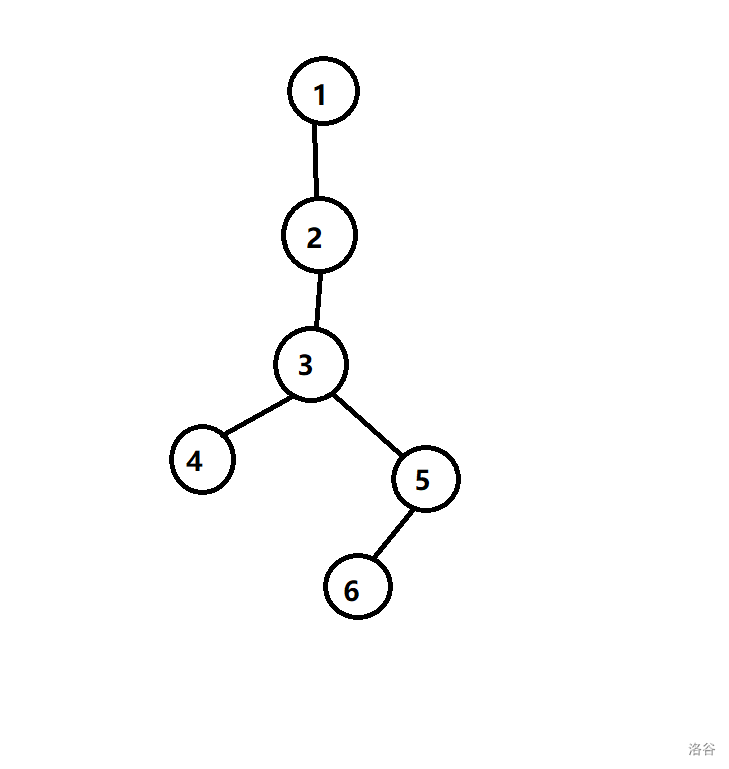
我们将其转化为一个差分数组。
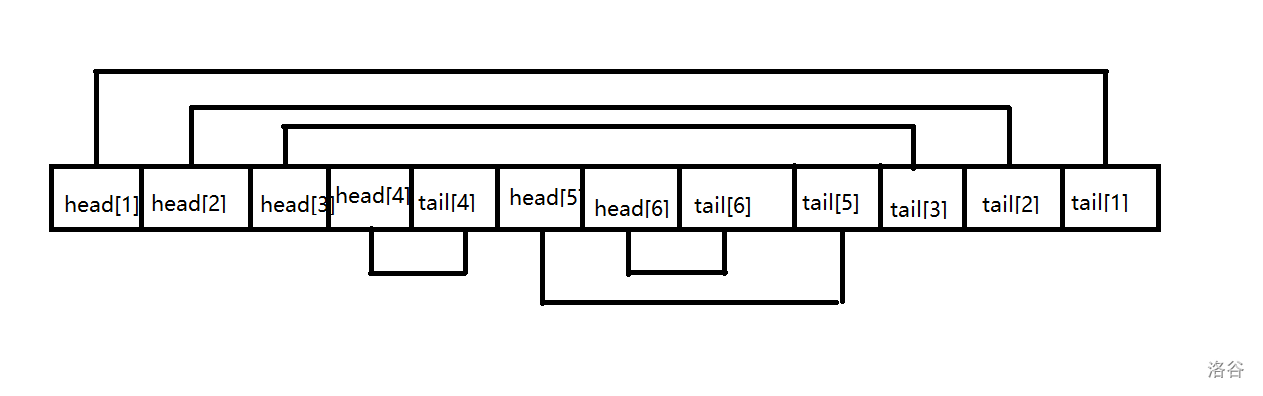
对于每次修改的 ,我们将 加上要加的值,在 上减去要加的值。
查询操作即为求区间和。
这样实现出来就是严格 的了。
具体实现看代码。
Code
#include<bits/stdc++.h> #define int long long #define maxn 1000005 #define maxm 1000005 using namespace std; inline int read(){ int x=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); return x*w; } int cnt,n,m,k,tot=1; int head[maxn],h[maxn],t[maxn],num[maxn],c[maxn]; struct e{int to,next;}edge[maxm]; int tree[maxn]; inline void addedge(int u,int v){ edge[++cnt].to=v; edge[cnt].next=head[u]; head[u]=cnt; } void dfs(int x){ h[x]=++tot; for(int i=head[x];i;i=edge[i].next) dfs(edge[i].to); t[x]=++tot; } inline int lowbit(int x){ return x&-x; } void add(int x,int k){ while(x<=tot){ c[x]+=k; x+=lowbit(x); } } int query(int x){ int sum=0; while(x){ sum+=c[x]; x-=lowbit(x); } return sum; } signed main(){ n=read();m=read(); tree[1]=read(); for(int i=2;i<=n;++i){ tree[i]=read(); int x=read(); addedge(x,i); } dfs(1); for(int i=1;i<=m;++i){ char opt; cin>>opt; if(opt=='p'){ int a=read(),x=read(); add(h[a]+1,x); add(t[a],-x); } else{ int a=read(); printf("%d\n",tree[a]+query(h[a])); } } return 0; }码风比较丑,还请见谅。
- 1
信息
- ID
- 7055
- 时间
- 1500ms
- 内存
- 64MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
