1 条题解
-
0
自动搬运
来自洛谷,原作者为

kyBWE
“时间会冲淡一切,但也只能冲淡。”搬运于
2025-08-24 22:32:34,当前版本为作者最后更新于2021-07-27 11:33:29,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
P7731题解
题意简述
起点为第 部电梯且横坐标为 (横坐标是 就及其别扭),终点为第 部电梯且横坐标为 ,换乘一次电梯花费 ZMB(注意所有电梯都是向右走的)。
题目分析
通过
简单的分析可以得知,如果能到达终点,那么至多需要换乘两次电梯。证明
- 情况一
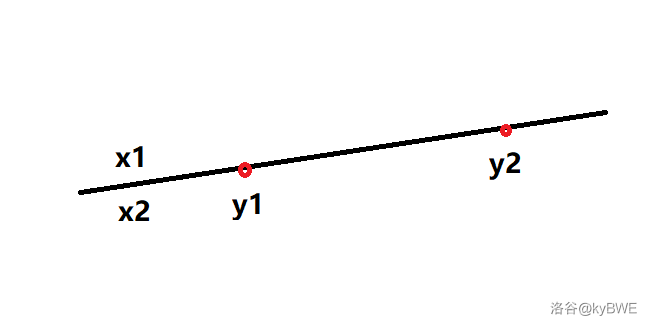
如果起点和终点在同一部电梯上(即在同一条直线上),并且起点在终点左侧,显然不需要换乘即可到达。
此时需要满足 且 (注意 可以等于 ,即起点和终点相同)。
- 情况二
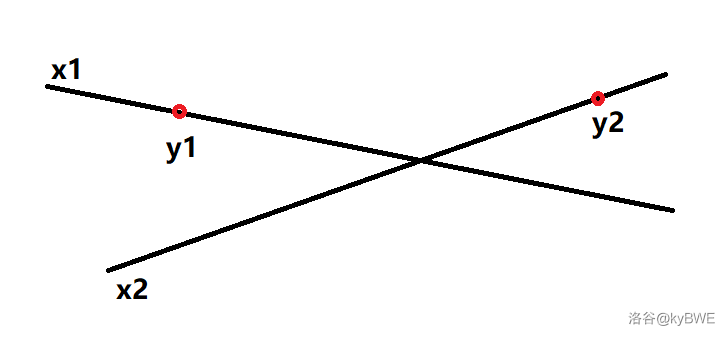
如果起点所在直线 和和终点所在直线 有交点且交点位于 之间,那么只需在交点处换乘一次即可到达。
此时需要满足 交点横坐标 。(如果 交点横坐标,那显然 在一条直线上,若为这种情况则已经在情况一中判断并输出结果了,所以不用担心误判)
顺便来推一下交点坐标:设交点坐标为 ,那么我们可以得到方程组
上减下可以得到
由此我们很容易就能得出交点横坐标 的关系式。
- 情况三
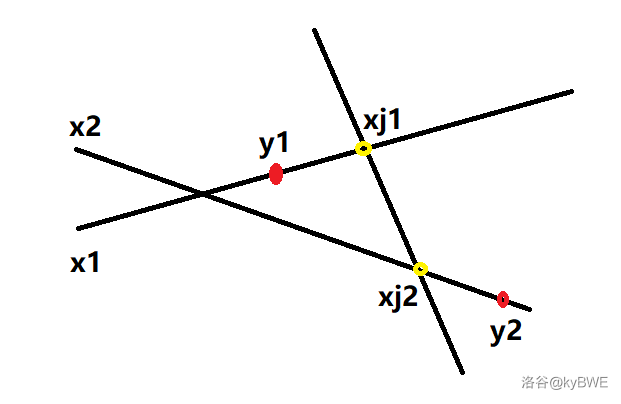
如果直线 和直线 的交点位于 两侧,有一条直线分别与 交于点 ,若两交点位于 之间且 ,那么只需在 和 两点各换乘一次即可到达
此时需要满足 ,所以我们可以枚举每一条直线的 和 ,并算出相应的 和 ,判断是否满足条件。
- 除上述三种情况外,其他情况都不能达到。
我们顺便来看一下不能到达的情况:
- 时显然不可能到达(因为电梯只能往右走)。
- 与 的交点位于 两侧,但没有一条直线与 的交点位于 之间。
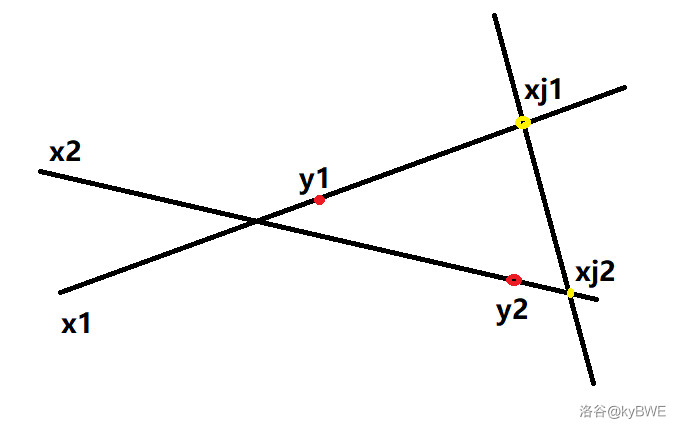
- 与 的交点位于 两侧,并且有一条直线与 的交点位于 之间,但是 。
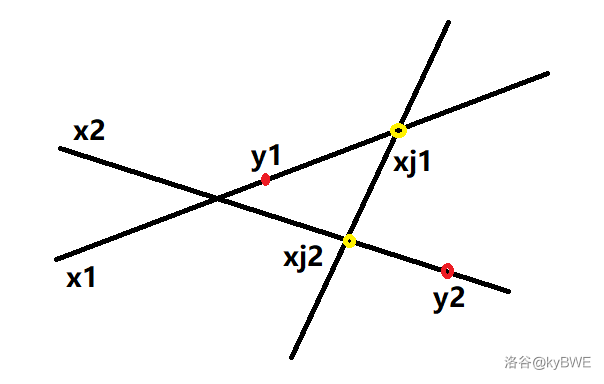
(因为电梯只能向右走,所以无法从 到达 )
最后附上AC代码
#include <iostream> using namespace std; int k[100005],b[100005]; int main() { int n,x1,x2,y1,y2; cin>>n; cin>>x1>>y1>>x2>>y2; for(int i=1;i<=n;i++) cin>>k[i]>>b[i]; if(x1==x2&&y1<=y2)//情况一 {//y1,y2在一条直线上 cout<<"0"; return 0;//直接结束程序防止后面误判 } //情况二 double x0=(b[x2]-b[x1])*1.0/(k[x1]-k[x2]); //先求出交点横坐标(注意要 *1.0把 k和 b转成 double型) if(y1<=x0&&y2>=x0) { cout<<"1"; return 0; } //情况三 for(int i=1;i<=n;i++)//枚举每一条直线 { double xj1=(b[i]-b[x1])*1.0/(k[x1]-k[i]); double xj2=(b[x2]-b[i])*1.0/(k[i]-k[x2]); //先求出两交点 xj1,xj2的横坐标 if(y1<=xj1&&xj1<=xj2&&xj2<=y2) { cout<<"2"; return 0; } } //若上述三种都不满足,则无法到达 cout<<"-1";//输出-1走人 return 0; }蒟蒻的第一篇题解qvq
- 情况一
- 1
信息
- ID
- 6767
- 时间
- 1000ms
- 内存
- 128MiB
- 难度
- 2
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
