1 条题解
-
0
自动搬运
来自洛谷,原作者为

xh39
**搬运于
2025-08-24 22:32:31,当前版本为作者最后更新于2021-08-18 06:14:28,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
注:文中所有 符号表示整除。设 表示所求排列。
从简单情况入手,一步步推,找规律。
如何确定 的位置?
由于 是最小的数,所以任何包含 的区间最小值都是 。
因此,在 的集合中出现个数可以作为1的位置。如下图:
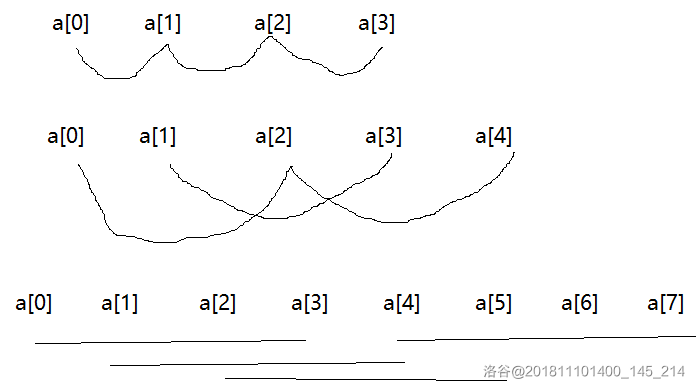
如上图第 的例子,查询长度为 的区间。若 在位置 则重复出现 次,在位置 则出现 次。
如上图 的例子,查询长度为 的区间。若 在位置 ,则出现次数依次为 。
如上图 的例子,查询长度为 的区间。若 在位置 ,则出现次数依次为 。
则出现次数为 , 那么 。
由与选取 的位置就是选取 的位置倒过来,所以实质上无影响。本篇题解默认选取 位置。
如何确定 的位置?
此时麻烦一些,因为包含 的区间最小值可能是 或 。
由于出现了 的区间最小值只可能是 。所以选完 以后, 的左右裂成了两个部分。所以判断到底是在哪个部分。然后就用之前的方法求解。
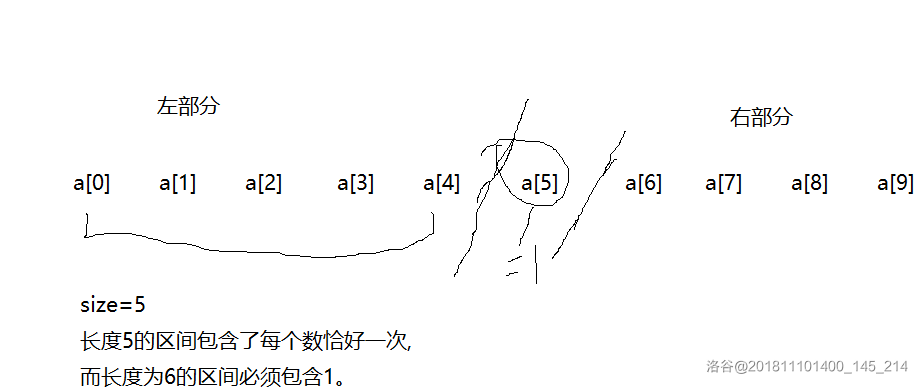
如何判断区间内是否有解?设区间长度为 ,则 中一定出现了 次最小值。而 中一定没有出现最小值。所以就判断 中 的出现次数。
若两部分内都有解,此时两部分长度相等,那么选取任意一部分都是等价的,本题解选取左部分。
确定完部分就与选取 时用同样的方法。
如何选取更多的数?(实现)
又可以将排列划分,现在有了 个部分。那么选取 也是一样的操作。但以上步骤不好直接模拟。因为不能快速找到区间。复杂度会超。
假设当前要选取 。考虑用一个链表记录当前已经确定了的数 1~。同时记录这个数选取的位置 。这样区间就是 [当前.id+1,下一个.id-1]。
这样一来,插入操作,查找操作都方便了很多。就可以在 的复杂度内出解。
参考代码
#include<iostream> using namespace std; struct i_am_aking_ioi{ int id,next; }_[1000005]; //链表。 int mark[1005][1005]; //mark[i][j]:长度为i的区间(S[i])内出现了几次j。 int main(){ int n,i,j,A,ykb; cin>>n; for(i=1;i<=n;i++){ for(j=i;j<=n;j++){ scanf("%d",&A); mark[i][A]++; } } _[0].next=n+1; _[0].id=-1; _[n+1].id=n; //初始化不能漏,一开始的区间是[0,n-1],由于区间是[now.id+1,next.id-1],所以要一开始要设为-1和n。 for(i=1;i<=n;i++){ //依次插入1~n for(j=0;j<=n;j=_[j].next){ //在每个区间内查找。 ykb=_[_[j].next].id-_[j].id; //区间长度 if(!mark[ykb][i]&&mark[ykb-1][i]){ _[i].id=_[j].id+mark[ykb+1>>1][i];//这个区间时从now.id+1开始编号的。所以需要加上_[j].id。同时+1-1抵消。 _[i].next=_[j].next; _[j].next=i; break; //已经找到,不需要再找。因为多个可行区间任选一个。 } } } for(i=_[0].next;i<=n;i=_[i].next){ cout<<i<<" "; } return 0; }月赛过去了这么久都没有题解。于是就写一篇。
- 1
信息
- ID
- 7091
- 时间
- 1000ms
- 内存
- 256MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
