1 条题解
-
0
自动搬运
来自洛谷,原作者为

xfrvq
**搬运于
2025-08-24 22:32:23,当前版本为作者最后更新于2022-12-20 09:30:31,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
这个修改实际上就是点加,询问就是点和。所以很好拆贡献。
操作分块,根号重构
因为询问的答案只会来自之前操作的修改。
我们对操作序列分块,块长 ,一次询问的答案分为:
类型一: 同块内在这个询问之前的修改
类型二:在这个询问之前的块的修改然后这个题的大体思路就是
- 第一类贡献计算:分别处理每个操作块(未重构部分)
- 第二类贡献计算:用一个全局数据结构
- 在扫完一个块就把这个块修改的贡献加进去(重构)
- 使用那个全局数据结构对每个点计算第二类贡献(已重构部分)
三维数点
指的是这样一个问题:对于若干个点 ,权 和若干询问 ,求出每个询问的三维偏序的权值和。
然后我们把这三个部分都转化为三维数点问题。然后三维数点就用二维分块做。
大概就是用一个全局二维分块,从小到大枚举 这一维,枚举完就把当前 这层的所有点加进二维分块,然后在用二维分块处理这一层的所有询问。
我们知道二维分块点修矩阵查和矩阵修点查都可做,并且可以把修改和询问的复杂度控制为 或 。
- 三维数点 个点 个询问,应该用 二维分块(显然)
- 三维数点 个点 个询问,应该用 二维分块(还是显然)
已重构部分
在每个询问块开始之前,(用一个能做三维数点的数据结构)维护好此时每个点的 权情况。
然后拿这个块的 次询问,和维护好的这 个点,做一次三维数点。
因为有 个块,所以留给每个块做这个三维数点的时间是 ,根据之前分析要用 二维分块。
重构部分
这部分相当于把 次修改,用 的时间累加到那个数据结构上。
我们还是三维数点,但是把询问当做点,点当做询问。三维数点做的是:对于每个点,有几个修改会对它产生影响。
对于这个三维数点而言,“点”数是询问数的 ,“询问”数是点数的 ,根据之前分析要用 二维分块。
未重构部分
这次对于每个询问,只需要考虑和它一个块内的修改。
所以我们大可以分析一个修改对一个询问的贡献,因为这样的一对只有 组。
- 考虑修改 ,询问 。(首先他俩得同块且修改在询问前面)
- 对于一个点 ,权值分别为 。
- 如果 ,产生 的贡献
- 综合起来,就是在 三维偏序中的点,他们的 之和乘上修改的 。
那就相当于
- 个点,权值为他们的 权。
- 次 的三维数点。
因为只用做一次,所以可以有 的时间。
三维数点
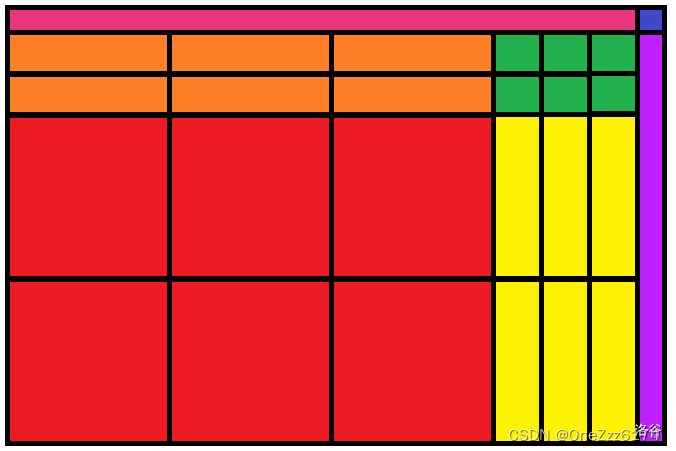
- 【整块】红色正方形
- 【整块】橙色长方形
- 【整块】黄色长方形
- 【整块】绿色正方形
- 【散块】紫色粉色长方形窄的边
- 【散块】蓝色长方形长和宽都
- 整块维护块和
- 散块借助 点 轴坐标互不相同 性质,所以看起来很大的散块只会有 的总点数,枚举点计算即可
然后是重头戏。未重构部分的三维数点。这个三维数点和上面那个结构不太一样。
原因是询问有 个,在随机的情况下每个 都对应着 级别询问。
如果按正常方法写,为了做到询问 就要拿点去匹配询问。
在这种情况下,依赖每个 坐标对应 询问的上述散块实现方法就不能用了。
所以我们整块散块分开做,整块还是维护那四种矩形的和。
对于上述整块,因为它只能查整块的和,所以我们不妨抽象地把一个 的东西叫做点,那单点修改和整块的询问就等价于在这个新的 $\dfrac n{n^{\frac12}}\times\dfrac n{n^{\frac12}}=n^{\frac12}\times n^{\frac12}$ 的结构上进行单点修矩阵查。
然后我们考虑散块,根据上面那个图,散块分为粉色、紫色的大散块,和蓝色的小散块。
因为小散块的定义,所以将原平面划分为 的小矩形,此时小散块必在 个小矩形的其中一个里面。
因为有 个点且点随机,所以期望到一个小矩形里只会有一个点,这样每个询问的小散块做到了 。
大散块就复杂一些,我讲讲紫色竖条怎么做,粉色横条类似。
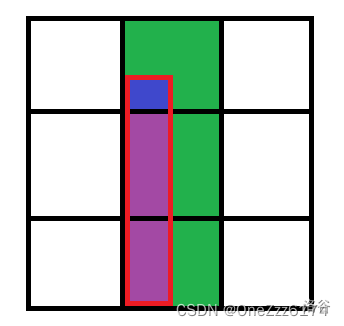
这里我们枚举每个像绿色这样的 矩形。每个询问的散块如红色所示,但是其中我们不管蓝色小散块,只算紫色竖条散块。
绿色矩形中会有 个点和 的询问,总共是 的操作。我们把这些操作按照 坐标排好序,在二维分块上做。
然后我们意识到现在原问题被简化了:
- 只有 个修改, 个询问
- 横轴因为是散块,只有 的范围
- 纵轴因为是整块,所以我们可以用块编号代替它的位置,也只有 的范围。
而根据我上面所说,二维分块做整块可以支持对一个 的矩形做单修区查。这里根据修改和询问的规模,采取 修改 查询的二维分块。
但是这些操作怎么排序?排序会多 。
对于点和询问分别的排序,我们把每个 值的点或询问用
vector装一下就排好了。然后它们在归并一下,或者说双指针一下,就可以按顺序来做了。
(2022.12.20)代码是五个月前写的,断断续续写了一个月,特别不可读。最近有点忙,等有空了我回来重构,重构完的代码会放到 这里。
因为没有代码。如有不理解欢迎私信询问。
- 1
信息
- ID
- 7057
- 时间
- 36000ms
- 内存
- 512MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
