自动搬运

查看原文

来自洛谷，原作者为

	hellhell 路漫漫其修远兮 吾将上下而求索

搬运于2025-08-24 22:32:10，当前版本为作者最后更新于2021-11-11 21:19:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[CEOI2005] Depot Rearrangement

题目描述

一家公司经营着 $n$ 个店铺，每个店铺都销售 $m$ 种不同的产品。该公司有一个大型仓库，产品在运送到商店之前在都会那里进行包装。每家商店将会收到相同数量的每种产品。因此，该公司将一定数量的相应产品分别包装到一个集装箱中，并用产品标识符标记该集装箱。产品由 $1$ 到 $m$ 的数字标识。

因此，在包装结束后，仓库中将会有 $n\cdot m$ 个集装箱，并且正好 $n$ 个集装箱贴有每种产品的对应标签。由于该仓库位于一个狭窄的建筑物内，所以集装箱排成了一排。但为了加快配送速度，仓库经理想要重新排列集装箱。由于将产品配送到商店是通过向每个商店发出一辆卡车来实现的，并且每辆卡车运载每种产品的一个集装箱，其合适的安排如下。该行最前部分 $m$ 个集装箱必须贴有不同的产品标签，该行的第二部分 $m$ 个集装箱必须贴有不同的产品标签，依此类推。

不幸的是，在这一行的尽头只有一个空闲的地方可以放置一个集装箱。因此，必须通过依次拿起集装箱并将其移动到空闲位置来进行重新排列。重新排列后，空闲位置也必须在行的末尾。目标是通过最少的移动以实现所需的重新排列。

计算需要最少移动多少次使得达成目标重排，输出最少的移动次数和具体的操作方案，每一步操作是形如 $(x,y)$ 的二元组，表示将 $x$ 位置上的集装箱移动到位置 $y$ 上。

样例输入：

5  6
4 1 3 1 6 5 2 3 2 3 5 6 2 1 4 5 6 4 1 3 2 4 5 5 1 2 3 4 6 6

样例输出：

8
9 31
18 9
10 18 
4 10
31 4
30 31
24 30
31 24

思路分析

不难发现，对于每一部分的集装箱，同种类只出现过一次的集装箱我们是不会动它的，我们会移动的是同种类出现次数大于 $1$ 的集装箱。

设 $t_{i,j}$ 表示 $[(i-1)\cdot m+1,i\cdot m]$ 区间内，种类为 $j$ 的集装箱出现的次数。

考虑构造二分图，左边点集为 $\{p_1,p_2,p_3\cdots,p_n\}$ 表示第 $i$ 段长度为 $m$ 的区间，右边点集为 $\{ q_1,q_2,q_3,\cdots q_m\}$ 表示集装箱的种类。

若 $t_{i,j}>1$，则在图中从 $p_i$ 向 $q_j$ 连接 $t_{i,j}-1$ 条有向边。

若 $t_{i,j}=0$，则在图中从 $q_j$ 向 $p_i$ 连接一条有向边。

对样例建立二分图

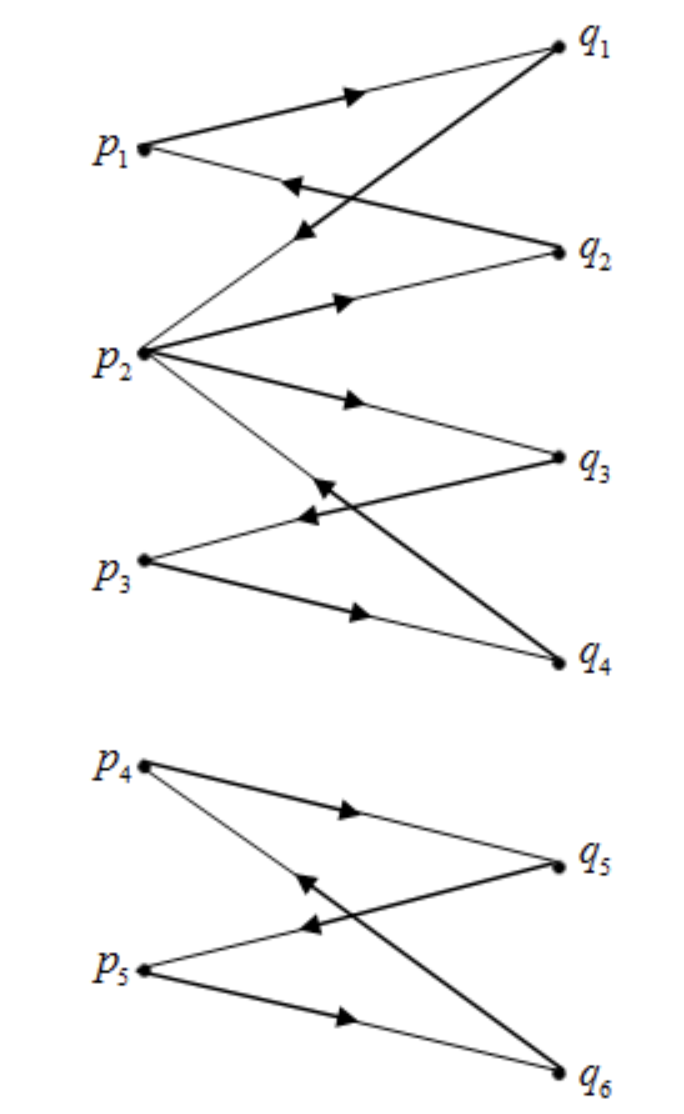
通过这样的方法构造出的二分图，其中一条从左到右再到左的路径为 $p_i\to q_j \to p_k$，表示将 $p_i$ 中种类为 $q_j$ 的集装箱放到 $p_k$ 的空位中。每次被放入集装箱的一段区间，一定要保证存在一个空位，为了保证操作次数最小，我们要尽可能地让 $n\cdot m+1$ 变成空地的次数最小。

每当我们在图中走完一条回路时，$n\cdot m+1$ 会为空，所以我们需要让找到的回路条数尽可能地少。也就是对于图中的每一个极大联通子图求一遍欧拉回路。然后按照欧拉回路构造方案即可。

可以证明图中每个子图一定存在欧拉回路。因为我们建边是根据 $t_{i,j}$ 来建边的，最终对集装箱安排好位置后，每一部分一定都有每种集装箱各 $1$ 个，所以初始状态，每多一个相同的种类的集装箱，就会少一种不同种类的集装箱。也就是每连接一条 $p_i\to q_j$ 的边同时也会伴随着连接一条 $q_k\to p_i$ 的边。有向图中，每一个点的入度与出度都相等，则一定存在欧拉回路。

具体的构造方案为，对于每一个极大联通子图任选一个点当起点，求欧拉回路。

记录经过的边的编号序列，倒序遍历序列，每遇到 $p_i\to q_j$ 的边就把 $q_j$ 移到空地上，同时更新空地的位置。

为什么要倒序枚举序列？每次的移动相当于在图中经过 $p_i\to q_j\to p_k$，每次移动都要保证 $q_j$ 想移动到的位置 $p_k$ 是空的，那么倒序枚举就可以保证 $p_k$ 一定是空的了，因为我们在移动 $p_i$ 中的集装箱时，上一步一定是移动了 $p_k$ 中的集装箱。 第一次移动集装箱，将集装箱移动到 $n\cdot m+1$ 上。最后再将 $n\cdot m+1$ 位置上的集装箱移动到现在的空地即可。

对于一个具有 $E$ 条边的极大联通子图，所需的操作次数为 $\frac{E}{2}+1$。

空间只有 $64MB$，实现时，记录每个集装箱位置的数组，要用 vector 来存。

代码实现

#include<bits/stdc++.h>
#define int long long

using namespace std;

inline int read() {
    int f = 1;
    int res = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        res = res * 10 + ch - '0';
        ch = getchar();
    }
    return res * f;
}

const int maxn = 410;

int n, m;
vector < int > pos[maxn][maxn];//用 vector 实现，不然会 MLE
int tot[maxn][maxn];

struct node {
    int from;
    int to;
    int next;
}
edge[maxn * maxn * 2];
int head[maxn << 1];
int cnt;

void add(int u, int v) {
    edge[++cnt].to = v;
    edge[cnt].from = u;
    edge[cnt].next = head[u];
    head[u] = cnt;
}

int que[maxn * maxn * 2], tag;
bool vis[maxn * maxn * 2];

void dfs(int now) {
    for (int i = head[now]; i; i = edge[i].next) {
        if (vis[i])
            continue;
        int v = edge[i].to;
        vis[i] = true;
        dfs(v);
        que[++tag] = i;
    }
}

struct ANS {
    int x;
    int y;
}
ans[maxn * maxn + maxn];
int len;

signed main() {
    n = read(), m = read();
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            int x = read();
            ++tot[i][x];
            pos[i][x].push_back((i - 1) * m + j);
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            for (int k = 1; k < tot[i][j]; k++) {
                add(i, j + n);
            }
            if (tot[i][j] < 1)
                add(j + n, i);
        }
    }
    for (int i = n + 1; i <= n + m; i++) {
        tag = 0;
        dfs(i);
        int to = n * m + 1;
        for (int i = 1; i <= tag; i++) {
            int u = edge[que[i]].from;
            int v = edge[que[i]].to;
            if (u <= n) {
                ans[++len].x = pos[u][v - n][--tot[u][v - n]];
                ans[len].y = to;
                to = ans[len].x;
            }
        }
        if (tag) {
            ans[++len].x = n * m + 1;
            ans[len].y = to;
        }
    }
    printf("%lld\n", len);
    for (int i = 1; i <= len; i++) {
        printf("%lld %lld\n", ans[i].x, ans[i].y);
    }
    return 0;
}