自动搬运

查看原文

来自洛谷，原作者为

	lmh .

搬运于2025-08-24 22:32:05，当前版本为作者最后更新于2022-03-29 12:51:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P7675 DOMINE

1.做法

COCI 出的题名字都是什么玩意

直接贪心显然不行，比如下面这组数据：

2 2
1 -100 -100
100 100 1

答案为 $202$，但是贪心会得到错误的 $101$。

正确的做法则是 $1\times2$ 骨牌的常见做法：状压 dp。

2.状压 dp

将几个状态压缩在一个 int 里面就是状压，比如：

几个球选或不选；

参加或不参加；

还有，棋盘中该位置是否为一个 $1\times2$ 骨牌的上半部分，也就是本题中的状态。

注意到宽度始终为 $3$，所以一共只有 $2^3=8$ 个状态。

时间复杂度 $O(nk)$，可以通过。

3.代码

将状态定义为一个二进制整数，从最低位开始数，第三，二，一位分别代表该行第一，二，三列是否为一个竖着放的骨牌的上半部分。

$f[i][j][k]$ 代表第 $i$ 行，已经放了 $j$ 个骨牌（半个骨牌也算），状态为 $k$。

有三种转移方法：

1：直接转移，不在该行放横着的骨牌；

2：在前两个位置放横着的骨牌；

3：在后两个位置放横着的骨牌。

放一张图片（转移处理的是中间一行）：

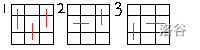
完整代码：

#include<bits/stdc++.h>
using namespace std;
long long n,a1,a2,a3,f[1001][1001][8],k,t,cnt,cnt2;
const int INF=-1e18;
inline int read(){
	char c=getchar();bool f=0;t=0; 
	while(!isdigit(c)) f|=c=='-',c=getchar();
	while(isdigit(c))t=(t<<1)+(t<<3)+(c^48),c=getchar();
	if(f)t=-t;return t;
}
int get(int state){
    return ((state&4)?a1:0)+((state&2)?a2:0)+((state&1)?a3:0);
    //特定状态覆盖的数之和
}
int cont(int state){
	return ((state&4)>>2)+((state&2)>>1)+(state&1);
//特定状态需要骨牌数
}
int q(int state,int i,int j){
    t=INF;cnt2=cont(state);
    if (j<cnt2) return INF; //骨牌不够
    for (int st=0,a;st<8;++st){
        if (st&state) continue; //一个格子上两张牌
        a=st|state;cnt=cont(a);
        if (j<cnt) continue; //骨牌不够
        if (!(a&3)&&j>cnt){
            t=max(t,get(a)+f[i-1][j-cnt2-1][st]+a2+a3);
            //第三种方式转移
        }
        if (!(a&6)&&j>cnt){
            t=max(t,get(a)+f[i-1][j-cnt2-1][st]+a2+a1);
            //第二种方式
        }
        t=max(t,f[i-1][j-cnt2][st]+get(a));
        //第一种方式
    }
    if (t-INF<30) return INF;
    return t;
}
int main(){
    scanf("%d%d",&n,&k);
    for (register int i=0;i<=k;++i) for (register int j=0;j<8;++j) f[0][i][j]=INF;
    f[0][0][0]=0;
    for (register int i=1;i<=n;++i){
        a1=read();
        a2=read();
        a3=read();//三个变量重复利用
        for (register int j=1;j<=k;++j){
            for (register int l=0;l<8;++l) f[i][j][l]=q(l,i,j);
        }
    }
    cout<<f[n][k][0];
    return 0;
}