[BalticOI 1996] A SQUARE AND A CIRCLE (Day 1)

0
15011418730 LV 7 @ 2025-8-24 22:31:53
自动搬运

查看原文

来自洛谷，原作者为

outcast
再见，只为再见

搬运于2025-08-24 22:31:53，当前版本为作者最后更新于2021-07-23 20:58:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

暂时还没有想到简单的做法

不过这个题是可以套板子的

事实上，我们不仅能做正方形与圆的面积交，还能做任意多边形与圆的面积交。

由于洛谷上没有相关的题目只好先写在这里了 ~~(虽然这是黄题)~~

前置芝士
- 向量的叉积：
如果你不知道什么是向量的叉积可以看这篇 blog，我这里直接给定理了：

设 $\Delta ABC$ 中的两条边 $\vec{a}=(x_1,y_1)$ ， $\vec{b}=(x_2,y_2)$ ，有 $S_{\Delta ABC}=\dfrac{|x_1y_2-x_2y_1|}{2}$ ，即 $\vec{a}\times \vec{b}=|\vec{a}||\vec{b}|\sin<\vec{a},\vec{b}>$

这个公式可以帮助我们利用向量快速求三角形面积

解析

我们知道任意一个多边形内选取一点，可以把多边形划分为多个三角形，像这样：

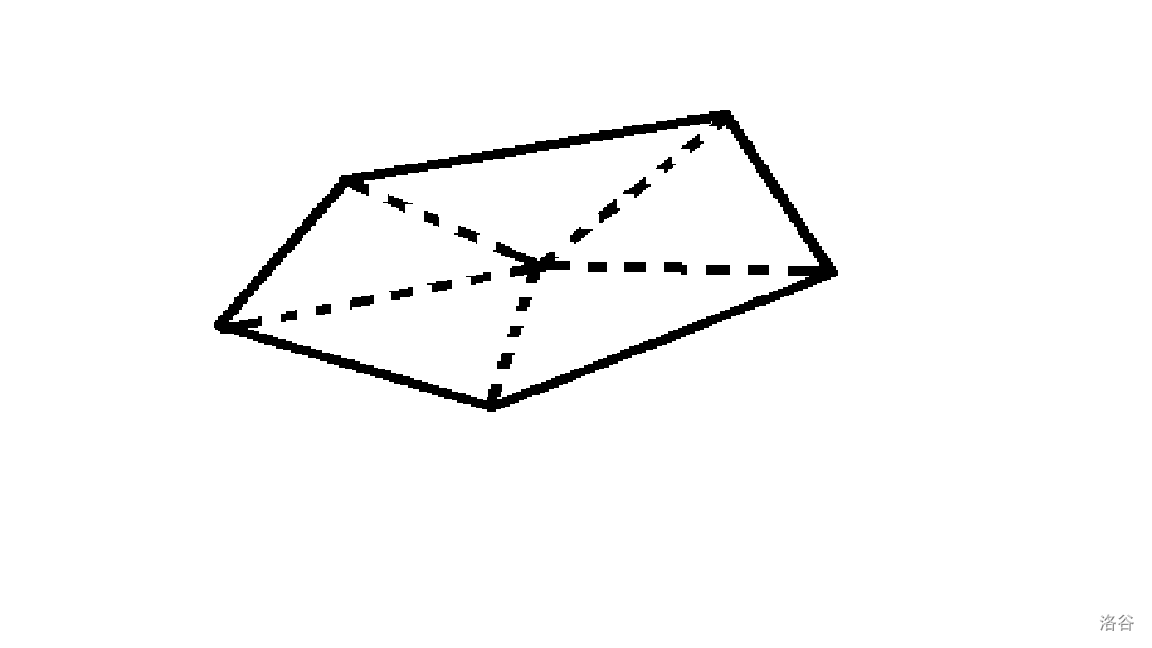
凹多边形也是可以的，你可以自己画一画（事实上平面内任意一点都可以把一个多边形划分为多个三角形）

所以问题就转化为了把一个多边形划分为多个三角形，然后分别求它与圆的面积交

新的问题产生了：我们该选哪一个点来划分呢？相信聪明的你已经猜到是圆的圆心了吧

划分的三角形有以下的情况：
- 三角形两边都在圆内
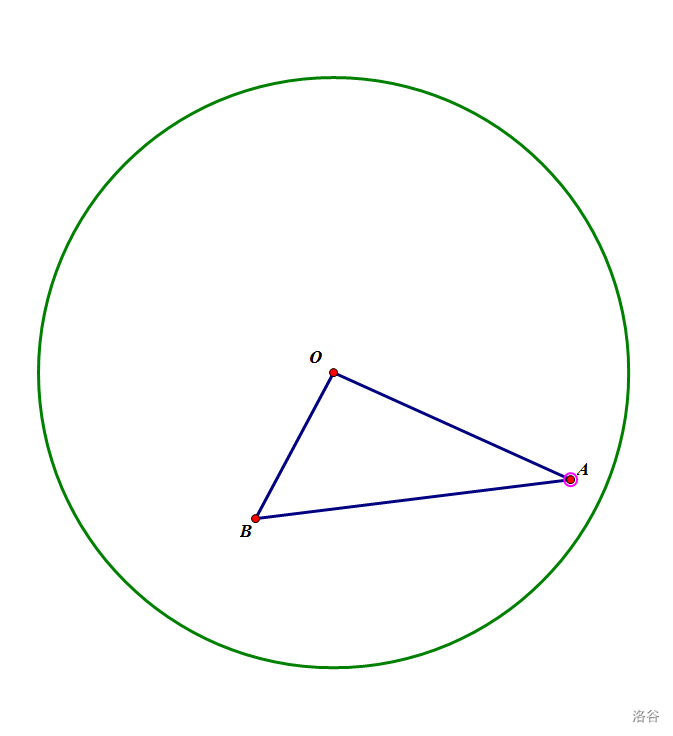
对于这种情况，直接计算三角形面积就行了
- 一边在圆内，一边在圆外
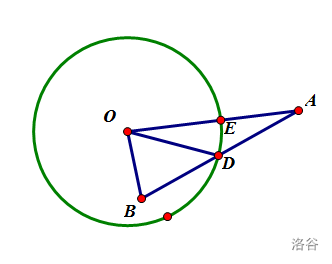
对于这种情况，计算 $\Delta OBD$ 和扇形 $OED$ 的面积
- 两边在圆外，且 $AB$ 与圆不相交
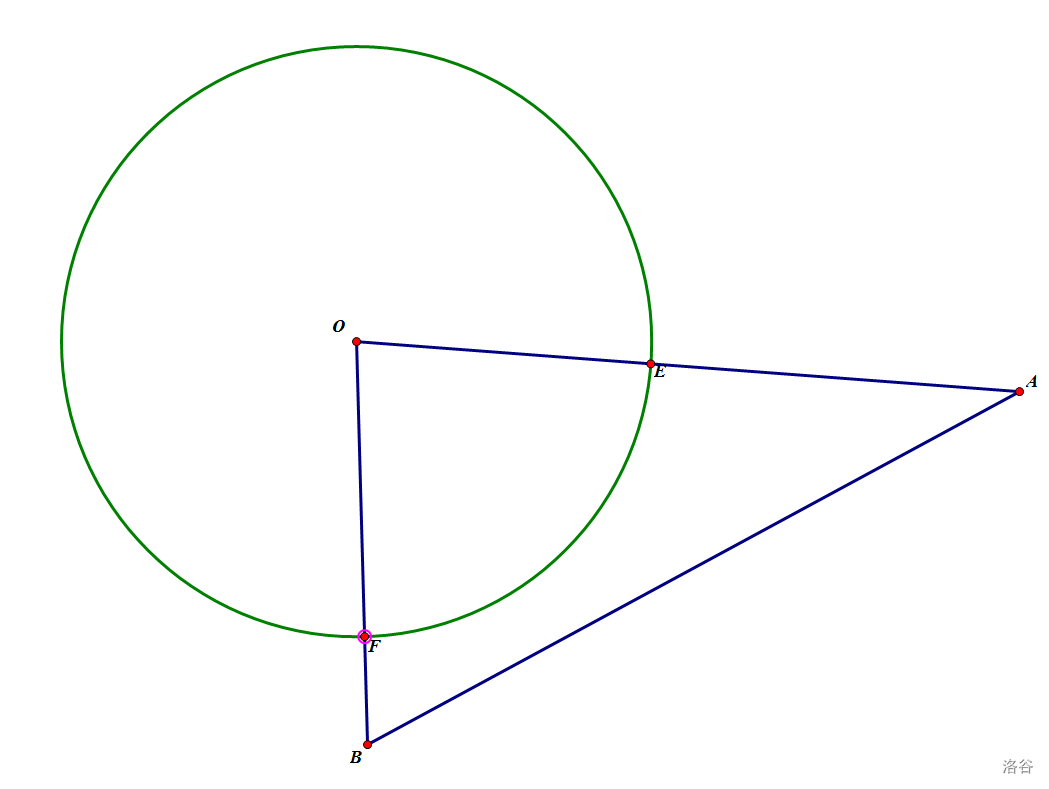
对于这种情况，计算扇形 $OEF$ 的面积
- 两边在圆外，且 $AB$ 与圆相交
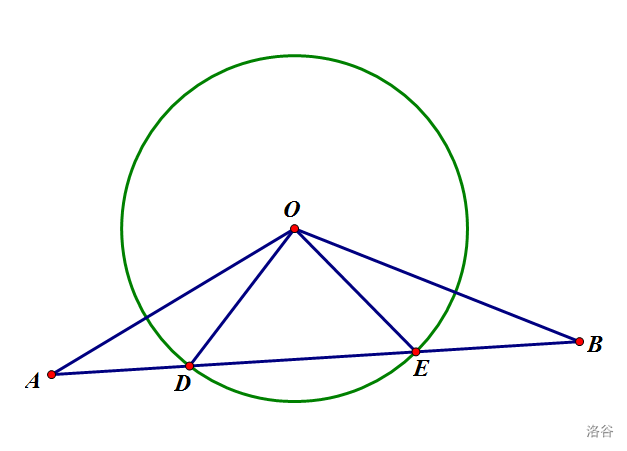
这个与第二种差不多求一个三角形和两个扇形的面积

（emm，这图片尺寸调不来啊>_<）

至此，我们相当于已经理论切掉了这道题，但是这道题的代码比较难写

代码实现

此题主要采用向量运算，来看看具体怎么实现
- 向量的基本运算
这个不用我多说了吧，看注释
```
double det(point a,point b){ return a.x*b.y-a.y*b.x;}//叉乘 
double dot(point a,point b){ return a.x*b.x+a.y*b.y;}//数量积（点乘） 
point operator *(point a,double t){ return point(a.x*t,a.y*t);}//数乘 
point operator +(point a,point b){ return point(a.x+b.x,a.y+b.y);}//加 
point operator -(point a,point b){ return point(a.x-b.x,a.y-b.y);}//减 
double Length(point A){return sqrt(dot(A,A));}//向量模长
```
- 判断一边是否在圆内
这个也非常简单，直接比较长度和圆的半径
```
int dcmp(double x){//这个函数是用来判断三角形上的向量是否在圆内（外） 
    if(fabs(x)<eps) return 0;
	if(x<0) return -1;
	return 1;
}
```
- 三角形两边都在圆内
直接叉乘算三角形面积
```
if(dcmp(DOA-C.r)<0&&dcmp(DOB-C.r)<0) return det(OA,OB)*0.5;//两边都在圆内，直接叉乘算面积 
```
（上面的 DOA，DOB 指的是向量 OA，OB 的模长，C.r 指圆的半径，下面不再赘述）
- 一边在圆内，一边在圆外
这个比较难，再来看一下图

我们先用叉乘求出 $\Delta OAB$ 的面积，我们要求 $\Delta OBD$ 的面积，就要算 $BD$ ，如何用已知量来表示 $BD$ ？

可以过 $O$ 做 $AB$ 的垂线交于 $M$ (由于图床空间不太够，我这里就不放图了，大家可以自己画一画)

推一下式子
$BD= \dfrac{(BM+MD)\times AB}{AB}$ $$BD= \dfrac{\vec{BO} \cdot \vec{BA}+AB \times MD}{AB} $$
问题转化为了用已知量求 AB $\times$ MD，于是
$AB\times MD= \sqrt{AB^2\times MD^2}$
勾股定理有
$AB\times MD= \sqrt{AB^2\times (OM^2+OD^2)}$
发现 $OD$ 正好是圆的半径， $OM=BO\sin\angle _{OBA}$ 于是
$$AB\times MD=\sqrt{AB^2r^2+AB^2BO^2\sin^2\angle _{OBA}} $$
发现 $AB\times BO\sin\angle _{OBA}$ 正好是 $\vec{BA}\times\vec{BO}$ ( 叉积 )

这样我们就把 $BD$ 用已知量表示出了
$$BD=\dfrac{\vec{OB}\cdot\vec{BA}+\sqrt{AB^2r^2+(\vec{BA}\times\vec{BO})(\vec{BA}\times\vec{BO})}}{AB} $$
再来计算扇形的面积，问题又转化为求 $\angle_{DOE}$

考虑三角形面积公式
$$S_{\Delta OAD}=\dfrac{OA\times OD\times\sin\angle_{DOE}}{2} $$
利用反正弦函数（arcsin）求出 $\angle_{DOE}$

具体看代码
```
    else if(DOB<r&&DOA>=r){//情况二 
        double x=(dot(BA,BO)+sqrt(r*r*DAB*DAB-det(BA,BO)*det(BA,BO)))/DAB;
        double TS=det(OA,OB)*0.5;
        return asin(TS*(1-x/DAB)*2/r/DOA)*r*r*0.5+TS*x/DAB;
        //这里比较难，要好好理解一下 
    }
    else if(DOB>=r&&DOA<r){
        double y=(dot(AB,AO)+sqrt(r*r*DAB*DAB-det(AB,AO)*det(AB,AO)))/DAB;
        double TS=det(OA,OB)*0.5;
        return asin(TS*(1-y/DAB)*2/r/DOB)*r*r*0.5+TS*y/DAB;
        //同上 
    }
```
- 两边在圆外，且 $AB$ 与圆不相交
这个就比较简单了，就是一个扇形的面积，反正弦函数求出角度即可

（需要注意的是反正弦函数只对 $[-\frac{\pi}{2},\frac{\pi}{2}]$ 有定义，所以对钝角的情况需要特判一下）
```
    else if(fabs(det(OA,OB))>=r*DAB||dot(AB,AO)<=0||dot(BA,BO)<=0){
        if(dot(OA,OB)<0){
            if(det(OA,OB)<0) return (-acos(-1.0)-asin(det(OA,OB)/DOA/DOB))*r*r*0.5;
            else return (acos(-1.0)-asin(det(OA,OB)/DOA/DOB))*r*r*0.5;
        }
        else return asin(det(OA,OB)/DOA/DOB)*r*r*0.5;
    }
```
- 两边在圆外，且 $AB$ 与圆相交
求法与第二种情况相似，相信聪明的你一定会做吧！
```
    else{
        double x=(dot(BA,BO)+sqrt(r*r*DAB*DAB-det(BA,BO)*det(BA,BO)))/DAB;
        double y=(dot(AB,AO)+sqrt(r*r*DAB*DAB-det(AB,AO)*det(AB,AO)))/DAB;
        double TS=det(OA,OB)*0.5;
        return (asin(TS*(1-x/DAB)*2/r/DOA)+asin(TS*(1-y/DAB)*2/r/DOB))*r*r*0.5 + TS*((x+y)/DAB-1);
    }
```
综上，我们就完成了所有情况的讨论

下面的代码给出了 n 边形与圆的面积交
```
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int maxn=200010;
const double eps=1e-12;
struct point{
    double x,y;
    point(){}
    point(double xx,double yy):x(xx),y(yy){}
};
struct Circle{
    point c; double r;
};
/*向量运算*/ 
double det(point a,point b){ return a.x*b.y-a.y*b.x;}
double dot(point a,point b){ return a.x*b.x+a.y*b.y;}
point operator *(point a,double t){ return point(a.x*t,a.y*t);}
point operator +(point a,point b){ return point(a.x+b.x,a.y+b.y);}
point operator -(point a,point b){ return point(a.x-b.x,a.y-b.y);}
double Length(point A){return sqrt(dot(A,A));}
 
int dcmp(double x){
    if(fabs(x)<eps) return 0;
	if(x<0) return -1;
	return 1;
}

/*计算圆与三角形面积交*/
double TriAngleCircle(Circle C, point A, point B){ 
    point OA=A-C.c,OB=B-C.c;
    point BA=A-B, BO=C.c-B;
    point AB=B-A, AO=C.c-A;
    double DOA=Length(OA),DOB=Length(OB),DAB=Length(AB),r=C.r;
    if(dcmp(det(OA,OB))==0) return 0;
    if(dcmp(DOA-C.r)<0&&dcmp(DOB-C.r)<0) return det(OA,OB)*0.5;
    else if(DOB<r&&DOA>=r){
        double x=(dot(BA,BO)+sqrt(r*r*DAB*DAB-det(BA,BO)*det(BA,BO)))/DAB;
        double TS=det(OA,OB)*0.5;
        return asin(TS*(1-x/DAB)*2/r/DOA)*r*r*0.5+TS*x/DAB;
    }
    else if(DOB>=r&&DOA<r){
        double y=(dot(AB,AO)+sqrt(r*r*DAB*DAB-det(AB,AO)*det(AB,AO)))/DAB;
        double TS=det(OA,OB)*0.5;
        return asin(TS*(1-y/DAB)*2/r/DOB)*r*r*0.5+TS*y/DAB;
    }
    else if(fabs(det(OA,OB))>=r*DAB||dot(AB,AO)<=0||dot(BA,BO)<=0){
        if(dot(OA,OB)<0){
            if(det(OA,OB)<0) return (-acos(-1.0)-asin(det(OA,OB)/DOA/DOB))*r*r*0.5;
            else return (acos(-1.0)-asin(det(OA,OB)/DOA/DOB))*r*r*0.5;
        }
        else return asin(det(OA,OB)/DOA/DOB)*r*r*0.5;
    }
    else{
        double x=(dot(BA,BO)+sqrt(r*r*DAB*DAB-det(BA,BO)*det(BA,BO)))/DAB;
        double y=(dot(AB,AO)+sqrt(r*r*DAB*DAB-det(AB,AO)*det(AB,AO)))/DAB;
        double TS=det(OA,OB)*0.5;
        return (asin(TS*(1-x/DAB)*2/r/DOA)+asin(TS*(1-y/DAB)*2/r/DOB))*r*r*0.5 + TS*((x+y)/DAB-1);
    }
}
point a[maxn];
int main(){
    double X,Y,r,ans=0; int N;
    cin>>N;
	rep(i,1,N) cin>>a[i].x>>a[i].y;
	cin>>X>>Y>>r;
	Circle C;
    C.c=point(X,Y); C.r=r;
    a[N+1]=a[1]; ans=0;
    rep(i,1,N) ans+=TriAngleCircle(C,a[i],a[i+1]);
    printf("%.2lf",fabs(ans));
}
```
这道题只是正方形与圆的面积交，稍微改一改上面的代码就可以了

后记

或许你不知道如何根据正方形不相邻的两点求出所有点的坐标（因为这个题不保证正方形的边与坐标轴平行）

可以看看这里

~~（其实是我太懒了）~~

还有一点 tips

细心的你一定发现我上面算叉积时没有加绝对值，而是在最后输出答案才加的，这样有什么好处呢？来看看下面一种情况

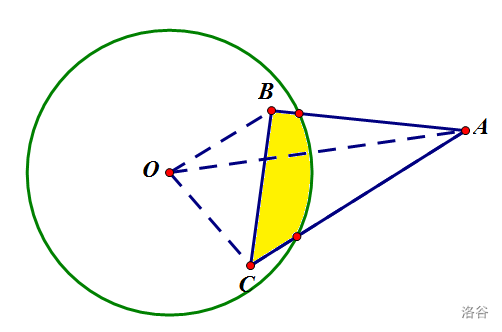
$\Delta ABC$ 与圆的面积交显然是黄色部分，但如果划分之后会发现 $\Delta OAB$ ， $\Delta OAC$ ， $\Delta OBC$ 分别与圆的面积交显然会大于黄色部分面积，算叉积时不取绝对值，就类似于容斥，可以避免上述情况