自动搬运

查看原文

来自洛谷，原作者为

	dead_X Still we rise

搬运于2025-08-24 22:31:27，当前版本为作者最后更新于2021-06-01 23:08:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

比 $\texttt{c}\color{red}\texttt{yffff}$ 那篇多描述了实现上的一些细节。

为何使用莫队

注意到如果给的是一个排列，那么问题就是区间逆序对，因此算法复杂度不会低于根号。

有两种做法：分块和二次离线莫队。

由于分块做法常数较大而且预处理之后整块散块不是很好算，我们考虑二次离线莫队。

要计算的贡献

因为两侧加入和删除都是等价的，考虑从最右侧加入一个数的贡献。

记加入的数下标为 $r$，它上一次出现为 $r'$，则 $(r',r)$ 中新出现的数会被计入贡献。

记 $f(l,r)$ 为 $[l,r]$ 中 $>a_r$ 的数的数量，贡献就可以拆成 $f(l,r)-f(l,r')$。

于是问题变成了 $n\sqrt m$ 次算 $f(l,r)$。

离线和最终问题

显然我们不能一个一个地储存 $n\sqrt m$ 个询问。

注意到在右侧插入的询问中 $l$ 都一样，而 $r$ 是一段连续的值，因此我们可以把这些值压成一段然后排序。

现在询问已经将 $l$ 从大到小排序了，我们再次简化问题：

• $n$ 次单点加。
• $n\sqrt m$ 次区间二维前缀和查询。
• 这些查询中，第二维的值只取决于第一维的值。

一个性质

在这里，我们可以将相同的 $a_r$ 直接加以区分，相同的数越靠左越大，让序列变成一个排列。

不难证明这样在题目中的查询里答案仍然正确。

这个性质会在最后一部分散块处理中用到。

人类智慧分块

我们考虑一些令人窒息的操作：

我们把询问的矩形分成 $n^{0.5}$ 个 $n^{0.75}\times n^{0.75}$ 的块。

再分成 $n^{0.75}$ 个 $n^{0.75}\times n^{0.5}$ 和 $n^{0.5}\times n^{0.75}$ 的块。

再分成 $n$ 个 $n^{0.5}\times n^{0.5}$ 的块。

于是一个询问大概可以被划分成这样：

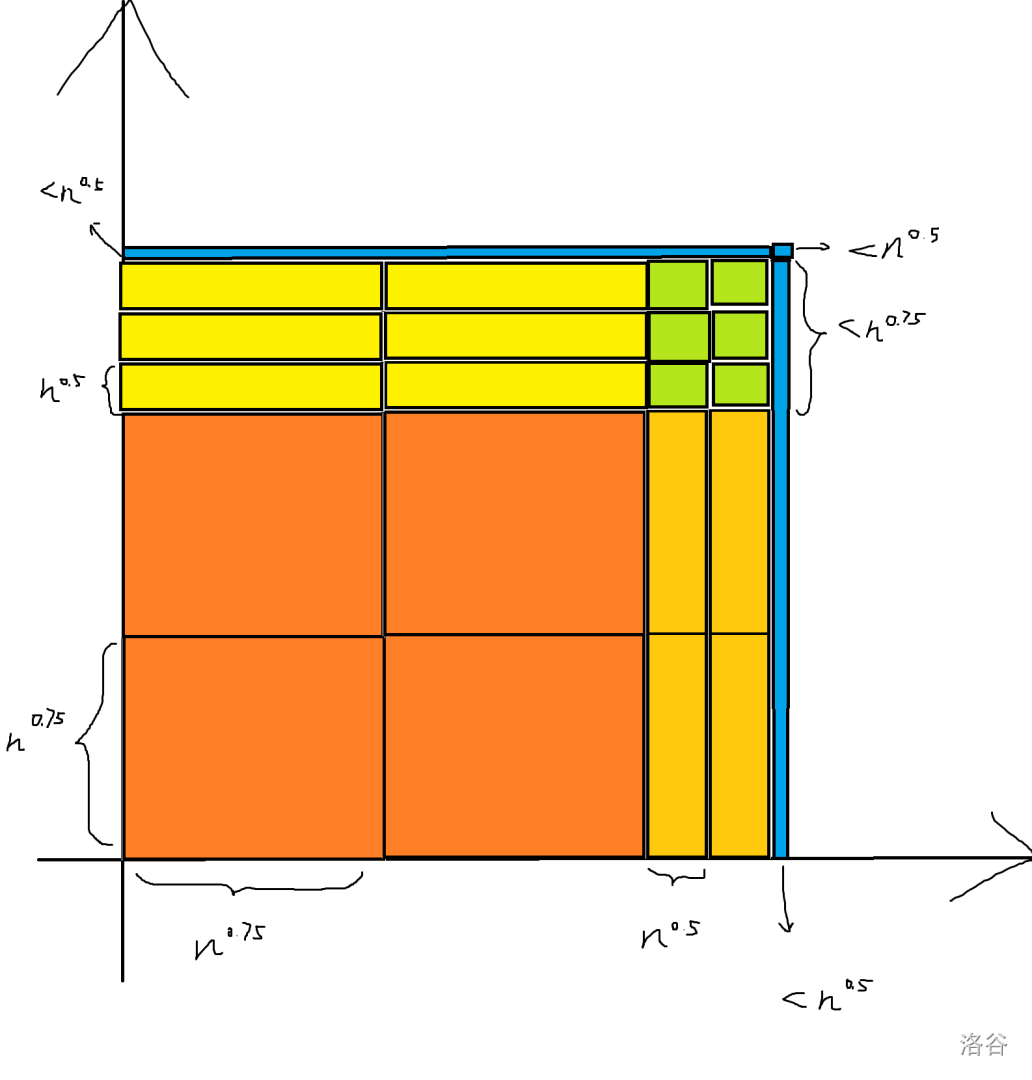
整块的处理方式

对于橙色的色块，我们暴力维护二维前缀和，复杂度为 $O(\sqrt n)-O(1)$。

对于黄，绿的色块，我们也暴力维护每个独立区域的二维前缀和。

由于一个独立区域仅包含 $\sqrt n$ 个块，因此可以做到 $O(\sqrt n)-O(1)$。

散块的处理方式

于是只剩下最后一部分了：蓝色的边角。

由于边角这一块的数量巨大，且绝大多数信息都为空，我们不能直接维护前缀和。

于是我们考虑反向维护：对于每个元素，它可能在哪些询问中从蓝色部分计入答案呢？

答案非常简单，询问符合条件当且仅当覆盖了这个元素的位置，且没有覆盖这个元素所在 $n^{0.5}\times n^{0.5}$ 块右上角的位置。

由于上文的那个性质，此时可以直接枚举两维 $\sqrt n$ 个可能合法的询问，如果满足则修改对应的值。

在查询时，直接加上第一维对应的值即可，因此这部分复杂度也是 $O(\sqrt n)-O(1)$

代码

至此本题得解，空间复杂度 $O(n+m)$，时间复杂度 $O(n\sqrt n+n\sqrt m)$。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define R(x) (n+1-x)
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
struct node
{
	int l,r,id,bl;
	bool operator<(const node&t)const{return (bl<t.bl)||(bl==t.bl&&r<t.r);}
}q[500003];
struct query
{
	int id,l,r,f;
};
vector<query> v1[500003],v2[500003];
int a[100003],pos[100003],lst[100003],nxt[100003];
ll ans[500003],lxl[500003];
int s0[30][30],s1[350][30],s2[30][350],s3[350][350],s4[110003];
int o[100003],b[100003],id[100003];
const int B1=320,B2=5760;
int n=read(),m,B;
void insert(int x)
{
	int y=b[x];
	for(int i=x/B2+1; i<20; ++i)
		for(int j=y/B2+1; j<20; ++j) 
			++s0[i][j];
	for(int i=x/B1+1,ir=(x/B2+1)*18; i<ir; ++i)
		for(int j=y/B2+1; j<20; ++j) 
			++s1[i][j];
	for(int i=x/B2+1; i<20; ++i)
		for(int j=y/B1+1,jr=(y/B2+1)*18; j<jr; ++j) 
			++s2[i][j];
	for(int i=x/B1+1,ir=(x/B2+1)*18; i<ir; ++i)	
		for(int j=y/B1+1,jr=(y/B2+1)*18; j<jr; ++j) 
			++s3[i][j];
	for(int i=x+1,ir=(x/B1+1)*B1; i<=n&&i<ir; ++i) (b[i]>y)&&(++s4[i]);
	for(int i=y+1,ir=(y/B1+1)*B1,sdt=(x/B1+1)*B1; i<=n&&i<=ir; ++i) 
	(id[i]>=sdt)&&(++s4[id[i]]);
}
void erase(int x)
{
	int y=b[x];
	for(int i=x/B2+1; i<20; ++i)
		for(int j=y/B2+1; j<20; ++j) 
			--s0[i][j];
	for(int i=x/B1+1,ir=(x/B2+1)*18; i<ir; ++i)
		for(int j=y/B2+1; j<20; ++j) 
			--s1[i][j];
	for(int i=x/B2+1; i<20; ++i)
		for(int j=y/B1+1,jr=(y/B2+1)*18; j<jr; ++j) 
			--s2[i][j];
	for(int i=x/B1+1,ir=(x/B2+1)*18; i<ir; ++i)	
		for(int j=y/B1+1,jr=(y/B2+1)*18; j<jr; ++j) 
			--s3[i][j];
	for(int i=x+1,ir=(x/B1+1)*B1; i<=n&&i<ir; ++i) (b[i]>y)&&(--s4[i]);
	for(int i=y+1,ir=(y/B1+1)*B1,sdt=(x/B1+1)*B1; i<=n&&i<=ir; ++i) 
	(id[i]>=sdt)&&(--s4[id[i]]);
}
int getsum(int x)
{
	int y=b[x]-1;
	return s0[x/B2][y/B2]+s1[x/B1][y/B2]+s2[x/B2][y/B1]+s3[x/B1][y/B1]+s4[x];
}
void solve1()
{
	for(int i=1; i<=n; ++i) ++o[a[i]];
	for(int i=1; i<=n; ++i) o[i]+=o[i-1];
	for(int i=1; i<=n; ++i) b[i]=o[a[i]]--;
	for(int i=1; i<=n; ++i) id[b[i]]=i;
	for(int i=n; i>=1; --i)
	{
		if(nxt[i]) erase(nxt[i]);
		insert(i);
		for(query t:v1[i]) 
		{
			ll s=0;
			for(int j=t.l; j<=t.r; ++j) 
			s+=getsum(j),(lst[j]>i)&&(s-=getsum(lst[j]));
			ans[t.id]+=s*t.f;
		}
	}
	return ;
}
void solve2()
{
	for(int i=1; i<=n; ++i) o[i]=0;
	for(int i=1; i<=n; ++i) ++o[a[i]];
	for(int i=1; i<=n; ++i) o[i]+=o[i-1];
	for(int i=1; i<=n; ++i) b[i]=o[a[i]]--;
	for(int i=1; i<=n; ++i) id[b[i]]=i;
	for(int i=1; i<=n; ++i)
	{
		if(lst[i]) erase(R(lst[i]));
		insert(R(i));
		for(query t:v2[i]) 
		{
			ll s=0;
			for(int j=t.l; j<=t.r; ++j) 
			s+=getsum(R(j)),(nxt[j]&&nxt[j]<i)&&(s-=getsum(R(nxt[j])));
			ans[t.id]+=s*t.f;
		}
	}
	return ;
}
signed main()
{
    for(int i=1; i<=n; ++i) a[i]=n+1-read();
    for(int i=1; i<=n; ++i) (pos[a[i]])&&(lst[i]=pos[a[i]]),pos[a[i]]=i;
    for(int i=1; i<=n; ++i) pos[i]=0;
    for(int i=n; i>=1; --i) (pos[a[i]])&&(nxt[i]=pos[a[i]]),pos[a[i]]=i;	
    m=read(),B=n/sqrt(m)+1;
    for(int i=1; i<=m; ++i) q[i].l=read(),q[i].r=read(),q[i].id=i,q[i].bl=q[i].l/B;
    sort(q+1,q+m+1);
    for(int i=1,l=1,r=1; i<=m; ++i) 
    {
    	if(r<q[i].r) v1[l].push_back((query){i,r+1,q[i].r,1}),r=q[i].r;
    	if(l>q[i].l) v2[r].push_back((query){i,q[i].l,l-1,1}),l=q[i].l;
		if(r>q[i].r) v1[l].push_back((query){i,q[i].r+1,r,-1}),r=q[i].r;
		if(l<q[i].l) v2[r].push_back((query){i,l,q[i].l-1,-1}),l=q[i].l;
    }
    solve1(),
    memset(s0,0,sizeof(s0)),
    memset(s1,0,sizeof(s1)),
    memset(s2,0,sizeof(s2)),
    memset(s3,0,sizeof(s3)),
    memset(s4,0,sizeof(s4)),
    reverse(a+1,a+n+1);
    for(int i=1; i<=n; ++i) a[i]=n+1-a[i];
    solve2();
    for(int i=1; i<=m; ++i) ans[i]+=ans[i-1];
    for(int i=1; i<=m; ++i) lxl[q[i].id]=ans[i];
    for(int i=1; i<=m; ++i) printf("%lld\n",lxl[i]);
	return 0;
}