自动搬运

查看原文

来自洛谷，原作者为

	b6e0_ ‪

搬运于2025-08-24 22:31:10，当前版本为作者最后更新于2021-03-15 23:14:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

官方题解。

本文中所有未经说明的函数都与题目中形式化题面的定义相同。设 $S(x,y)$ 表示 $x$ 到 $y$ 的简单路径上所有节点的点权和（$x$ 和 $y$ 也算在内），$P(x,y)$ 表示 $x$ 到 $y$ 的简单路径上所有节点的点权积（$x$ 和 $y$ 也算在内），$siz_u$ 表示以 $u$ 为根的子树节点个数，根是哪个节点见语境。

先考虑对于确定的 $r$，确定的 $u$，怎么计算 $W(u)=\sum_{v=1}^nf(v,u)$。

$f$ 的定义就是一个分段函数的形式，所以考虑对于 $x\in A_u$ 和 $x\not\in A_u$ 的两种 $x$ 分别求和。$f(x,u)$ 中情况 $x\in A_u$ 的式子可以做出如下转换：

$$\begin{aligned}f(F(x),u)+a_x&=f(F(F(x)),u)+a_{F(x)}\\&=f(F(F(F(x))),u)+a_{F(F(x))}+a_{F(x)}+a_x\\&\cdots\\&=S(x,u)+f(F(u),u)\end{aligned} $$

于是，处理出 $SS_u$ 表示 $\sum_{v\in A_u}S(v,u)$，以 $u$ 为根的子树中节点的 $f$ 和就是 $SS_u+siz_u\cdot f(F(u),u)$。这里给出 $SS$ 的递推式：$SS_u=siz_ua_u+\sum_{v\in B_u,v\ne F(u)}SS_v$。

对于 $x\not\in A_u$ 的情况，以 $F(u)$ 为根，$D(x,u)$ 为节点 $x$ 的深度，拎起一棵树，直接求即可。

当 $u$ 变化时，以 $u$ 为根的子树中节点的 $f$ 和仍然可以用 $SS_u+siz_u\cdot f(F(u),u)$：首先要对于所有节点 $u$ 求出 $SS_u$ 和 $siz_u$，然后对于 $f(F(u),u)$ 的计算，考虑在下图中，将 $u$ 换成它的一个孩子 $v$，$f(F(u),u)$ 会发生什么变化：

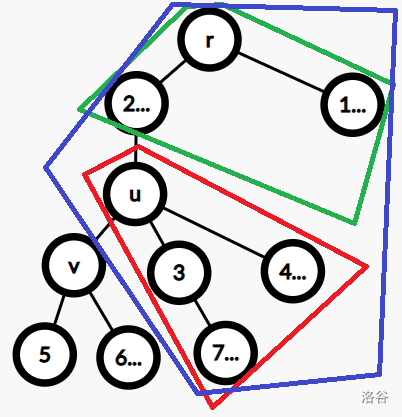
观察图，原来子树外的部分是绿框，现在是蓝框，发现多的部分就是 $u$ 除 $v$ 以外其他孩子的子树和 $u$，也就是图中红色框的部分，按照原来层次传上来的贡献。于是，对于每个节点 $x$，求出 $SP_x=a_x\cdot\max_{y\in B_x,y\ne F(x)}SP_y$，在每次准备将 $u$ 换成 $v$ 时，对于 $u$ 的所有孩子的 $SP$ 按照 dfs 顺序求一个前缀 $\max$ 和后缀 $\max$，转移即可。

到现在，以一次 $\mathcal O(n)$ 的复杂度，求出了 $C(r)$，总时间复杂度是 $\mathcal O(n^2)$，还不够优秀，考虑继续优化。因为这里是对每个节点求一个值，根据套路，考虑换根，即考虑根从 $r_1$ 变到 $r_2$ 时答案的变化。

此处先考虑 $x\not\in A_u$。注意到根 $r$ 的变化，除了 $u=r_1$ 和 $u=r_2$，影响不到你拎起来的这棵树。这棵拎起来的树只跟 $F(u)$，$D(x,u)$ 有关，而这些东西，除了 $u=r_1$ 和 $u=r_2$，在换根时没有变化。类似地，$x\in A_u$ 的情况，只跟子树中有哪些节点有关，除了 $u=r_1$ 和 $u=r_2$，其他的子树都没有变化！于是，用上面的计算方法，只需要特殊处理 $u=r_1$ 和 $u=r_2$ 时的 $W(u)$。我太懒了就没有画图。

处理 $u=r_1$ 和 $u=r_2$ 时的 $W(u)$ 需要算出一些额外的值：$AS_x$ 表示树中所有节点到 $x$ 路径上的点权和，即 $AS_x=\sum_{y=1}^nS(x,y)$，这个值可以用换根 dp 求出；其他的值可以用类似上面的方法求出。总时间复杂度 $\mathcal O(n)$。代码（建议复制到 IDE 里看）：

#include<bits/stdc++.h>
using namepace std;
const int mod=998244353;
vector<int>g[500010];
int n,siz[500010];
long long a[500010],ss[500010],as[500010],sp[500010],ssp[500010],uans[500010],ans[500010];//ssp为子树内sp的和，uans[x]表示当r=1时的W(r)
inline int read()//快读
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9')
		c=getchar();
	while(c>='0'&&c<='9'){
		x=(x<<3)+(x<<1)+c-'0'; c=getchar();
	}
	return x;
}
inline void write(int x)//快写
{
	if(!x){
		putchar('0'); putchar('\n');
		return;
	}
	while(x<0) x+=mod;
	int sta[10],tp=0;
	while(x){
		sta[++tp]=x%10; x/=10;
	}
	while(tp)
		putchar(sta[tp--]+'0');
	putchar('\n');
}
void dfs(int x,int f)//求出siz,ss,sp,ssp
{
	siz[x]=1;
	sp[x]=-1;
	for(int i=0;i<g[x].size();i++)
		if(g[x][i]!=f)
		{
			dfs(g[x][i],x);
			siz[x]+=siz[g[x][i]];
			ss[x]=(ss[x]+ss[g[x][i]])%mod;
			sp[x]=max(sp[x],sp[g[x][i]]);
		}
	ss[x]=(ss[x]+siz[x]*a[x]%mod)%mod;
	if(sp[x]==-1)
		ssp[x]=sp[x]=a[x];
	else
		ssp[x]=sp[x]=sp[x]*a[x]%mod;
	for(int i=0;i<g[x].size();i++)
		if(g[x][i]!=f)
			ssp[x]=(ssp[x]+ssp[g[x][i]])%mod;
}
void dp1(int x,int f,long long nf,long long ns)//求出uans,ans[1],as
{
	uans[x]=(ss[x]+nf*siz[x]%mod+ns)%mod;
	ans[1]=(ans[1]+uans[x])%mod;
	if(x!=1)
		as[x]=(as[f]-a[f]*siz[x]+a[x]*(n-siz[x])%mod)%mod;
	int i,pt=0,lt=g[x].size()-2;
	vector<long long>pm,lm;//前缀，后缀最大值
	if(x==1)
		lt++;
	pm.push_back(0);
	lm.push_back(0);
	for(i=0;i<g[x].size();i++)
		if(g[x][i]!=f)
			pm.push_back(max(pm.back(),sp[g[x][i]]));
	for(i=g[x].size()-1;~i;i--)
		if(g[x][i]!=f)
			lm.push_back(max(lm.back(),sp[g[x][i]]));
	for(i=0;i<g[x].size();i++)
		if(g[x][i]!=f)
		{
			dp1(g[x][i],x,max(max(nf,1ll),max(pm[pt],lm[lt]))*a[x]%mod,(ns+ssp[x]-ssp[g[x][i]]-sp[x]+max(max(nf,1ll),max(pm[pt],lm[lt]))*a[x]%mod)%mod);
			pt++;
			lt--;
		}
}
void dp2(int x,int f)//求出ans
{
	ans[x]=(ans[f]-as[f]-uans[x]+as[x]+ssp[x]+sp[x]*(n-siz[x])%mod+as[f]-ss[x]-a[f]*siz[x]%mod)%mod;
	for(int i=0;i<g[x].size();i++)
		if(g[x][i]!=f)
			dp2(g[x][i],x);
}
int main()
{
	int i,x,y;
	n=read();
	for(i=1;i<=n;i++)
		a[i]=read()%mod;//进来要先%！否则在比较大小时会出问题
	for(i=1;i<n;i++)
	{
		x=read();
		y=read();
		g[x].push_back(y);
		g[y].push_back(x);
	}
	dfs(1,0);
	as[1]=ss[1];
	dp1(1,0,0,0);
	for(i=0;i<g[1].size();i++)//不想让节点1再转移一遍，所以直接对1的孩子做
		dp2(g[1][i],1);
	for(i=1;i<=n;i++)
		write(ans[i]);
	return 0;
}