自动搬运

查看原文

来自洛谷，原作者为

	zjjws Dirty Deeds Done Dirt Cheap

搬运于2025-08-24 22:31:07，当前版本为作者最后更新于2021-05-02 14:19:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题链

非常妙的分讨构造题。

---

Solution 1

$n=1\ |\ m=1$

此时只能一路冲到底，判一下与另一个的大小关系即可。

---

Solution 2

$k\ge n\ |\ k\ge m$

我们就可以对短的那一维，每次冲到底，然后换下一行/列。

---

inline void work_1()
{
    if(n==1){if(k<m){puts("NO");return;}puts("YES");for(int i=1;i<m;i++)putchar('R');puts("");puts("1 1");return;}
    puts("YES");for(int i=1;i<=m;i++){for(int j=1;j<n;j++)putchar((i&1)?'D':'U');if(i!=m)putchar('R');}puts("");
    printf("%d %d\n",1,1);return;
}
inline void work_2()
{
    if(m==1){puts("NO");return;}
    puts("YES");for(int i=1;i<=n;i++){for(int j=1;j<m;j++)putchar((i&1)?'R':'L');if(i!=n)putchar('D');}puts("");
    printf("%d %d\n",1,1);return;
    return;
}

这前两个 Solution 判完后，显然 $k\le 2$ 无解。

可以自己手玩一下。

---

Solution 3

$k\ge 5$

此时有一种构造，就是直接每次消 $2/3$ 行/列，其中前面的 $2,3$ 取决于另一维的奇偶性。

具体的，拿消列举例，是这样的两个图形：

行为奇数时：

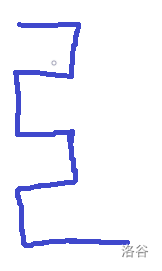
行为偶数时：

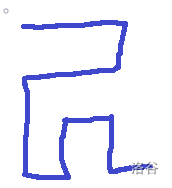
会注意到这样之后会变成一个规模更小的子问题。

递归的边界条件是 $m=2|3$，此时按照前面两个 Solution 的跑法即可。

但是涉及到每次切换子问题会有一个 前面积攒 的连续走的步数，当 $k\ge 5$ 时，最坏的情况也是能接受的。

大家可以手玩一下。

---

这里涉及到子问题，会注意到如果写一堆 if 语句来判断当前出发点是在矩阵的哪个角落会非常地屎。

我是在跑的时候默认出发点在左上角，但是存储一下当前的反转状态，然后在输出的时候转化一下就好。

struct gyq
{
    char c[4];
    // 0 1 2 3
    // 上下左右
    inline void init(){c[0]='U';c[1]='D';c[2]='L';c[3]='R';return;}
    inline void change(int typ)
    {
        if(typ==1||typ==3)jh(c[2],c[3]);
        if(typ==2||typ==3)jh(c[0],c[1]);
        return;
        //typ 0 1 2 3 分别对应左上，右上，左下，右下
    }
}tp[4];

inline void work_stp(int n,int m,int typ)
{
    if(n<=3){for(int i=1;i<=m;i++){for(int j=1;j<n;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}return;}
    if(m<=3){for(int i=1;i<=n;i++){for(int j=1;j<m;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}return;}
    if(n&1)
    {
        for(int i=1;i<=n;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}
        putchar(tp[typ].c[3]);
        int nxt;if(typ==0)nxt=2;if(typ==1)nxt=3;if(typ==2)nxt=0;if(typ==3)nxt=1;work_stp(n,m-2,nxt);
        return;
    }
    if(m&1)
    {
        for(int i=1;i<=m;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}
        putchar(tp[typ].c[1]);
        int nxt;if(typ==0)nxt=1;if(typ==1)nxt=0;if(typ==2)nxt=3;if(typ==3)nxt=2;work_stp(n-2,m,nxt);
    }
    return;
}

这里是暴力跑奇的，如果初始 $n,m$ 都为偶，就跑一遍前面说的那种就可以调用这个函数了。

---

Solution 4

$n,m$ 都为偶数。

并没有这个 subtask 但是这个部分非常关键。

因为会发现我们的瓶颈在于：递归到最后的边界时，前面转化子问题时积攒的步数会和边界时暴力冲到底的步数相加。

最坏的情况，就是前面跑了一个 行为奇数 的子问题转化，积攒了两步到达当前子问题，然后列还剩 $3$，只能暴力跑，相加得到的最大连续步数为 $4$。

此时 $k\ge 5$ 才能有解。

但是如果行列都是偶数时，我们存在一种更优秀的构造：

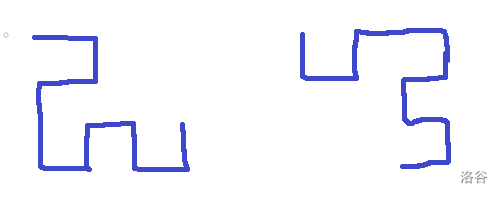
这样每次消去两行两列。

为什么要这两种都画呢？因为它们都有用。当 $n\ge m$ 时，我们会调用第一种跑法，这样最后暴力跑的时候就不会有步数的相加。第二种跑法对应另一种 Case。

这样可以达到 $k\ge 3$ 时都有解。

$k\le 2$ 时无解已经判过了。

---

inline void work_zjj(int n,int m,int typ)
{
    if(m==2){for(int i=1;i<=n;i++){for(int j=1;j<m;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}return;}
    for(int i=1;i<=n-2;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}
    putchar(tp[typ].c[1]);putchar(tp[typ].c[3]);putchar(tp[typ].c[0]);putchar(tp[typ].c[3]);
    for(int i=3;i<=m;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}
    putchar(tp[typ].c[0]);int nxt=3-typ;work_zjj(n-2,m-2,nxt);
    return;
}
inline void work_gyq(int n,int m,int typ)
{
    if(n==2){for(int i=1;i<=m;i++){for(int j=1;j<n;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}return;}
    for(int i=1;i<=m-2;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}
    putchar(tp[typ].c[3]);putchar(tp[typ].c[1]);putchar(tp[typ].c[2]);putchar(tp[typ].c[1]);
    for(int i=3;i<=n;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}
    putchar(tp[typ].c[2]);int nxt=3-typ;work_gyq(n-2,m-2,nxt);
    return;
}

---

Solution 5

$n,m$ 无限制。

会注意到：我们只要能够转移到 $n,m$ 都为偶数的子问题，就可以轻松地解决此题了。

回想到前面 Solution 3 中消 3 行/列 的操作，它可以改变另一维的奇偶性。

那么对于 $n,m$ 只有一个奇数的情况，我们就可以跑一遍这个得到双偶的 Case。

如果都是奇数呢？

我们可以出发点选择 $(3,1)$，然后跑一遍：

这样就可以把 $m$ 变成偶数，然后再跑一遍 Solution 3 中的方法把 $n$ 也变成偶数。

于是本题就轻松做完了（

---

inline void work_6()
{
    puts("YES");
    if(m&1)
    {
        if(n&1)
        {
            for(int i=1;i<=n-2;i++){for(int j=1;j<3;j++)putchar(tp[0].c[3-(i&1)]);if(i!=n)putchar(tp[0].c[1]);}
            for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[0].c[i&1]);putchar(tp[0].c[3]);}
            m-=3;
            for(int i=1;i<=m-2;i++){for(int j=1;j<3;j++)putchar(tp[2].c[i&1]);if(i!=m)putchar(tp[2].c[3]);}
            for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[2].c[2+(i&1)]);putchar(tp[2].c[1]);}
            n-=3;{if(n>=m)work_zjj(n,m,3);else work_gyq(n,m,3);}
            puts("");puts("1 3");
        }
        else 
        {
            for(int i=1;i<=n-2;i++){for(int j=1;j<3;j++)putchar(tp[0].c[2+(i&1)]);if(i!=n)putchar(tp[0].c[1]);}
            for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[0].c[i&1]);putchar(tp[0].c[3]);}
            m-=3;
            if(n>=m)work_zjj(n,m,2);else work_gyq(n,m,2);
            puts("");puts("1 1");
        }
        return;
    }
    if(n&1)
    {
        for(int i=1;i<=m-2;i++){for(int j=1;j<3;j++)putchar(tp[0].c[i&1]);if(i!=m)putchar(tp[0].c[3]);}
        for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[0].c[2+(i&1)]);putchar(tp[0].c[1]);}
        n-=3;if(n>=m)work_zjj(n,m,1);else work_gyq(n,m,1);puts("");puts("1 1");return;
    }
    else {if(n>=m)work_zjj(n,m,0);else work_gyq(n,m,0);}puts("");puts("1 1");return;
    return;
}