自动搬运

查看原文

来自洛谷，原作者为

	lyfqwq AFOed.

搬运于2025-08-24 22:30:44，当前版本为作者最后更新于2021-05-25 20:53:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本蒟蒻看到各位大佬的代码都这么的高端大气，那么就由我来一发朴实无华的题解来弥补你谷的空缺吧。

【朴实无华的分析】

十分显然的 一道 Kruskal 最小生成树题。

题意还是比较容易读懂的，主要就是关于题意转换比较难想，让我们看一下具体操作，究竟发生了些什么。

如以下问题所述：存在两个节点 $pi$ ， 每个节点有 $v_1, v_2, v_3, v_4$ 四个传送门， 两个节点的关系如下图。

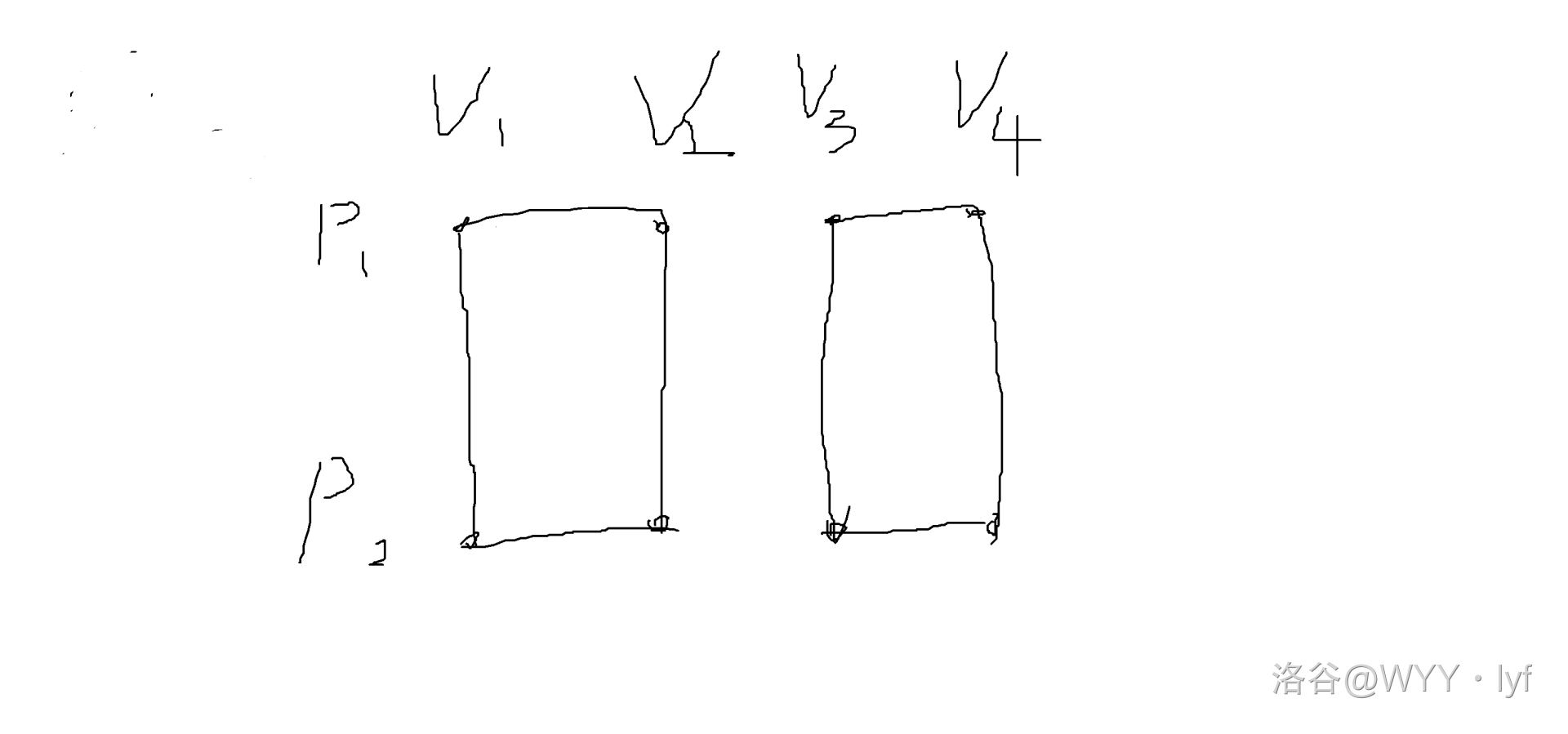
那么很显然， 你可以从 $p_1v_1$ 进入到达 $p_2v_1, p_2v_2$ 这两个位置, 但是你无法到达 $p_2$ 的另外两个位置。

那么怎么办呢？

没错，就是通过改变传送门的位置从而使所有的位置组成一个连通块。很显然图中存在两个环， 我们需要将它变成一个环，那么就可以达到目的了。

操作完之后大概是这个样子：

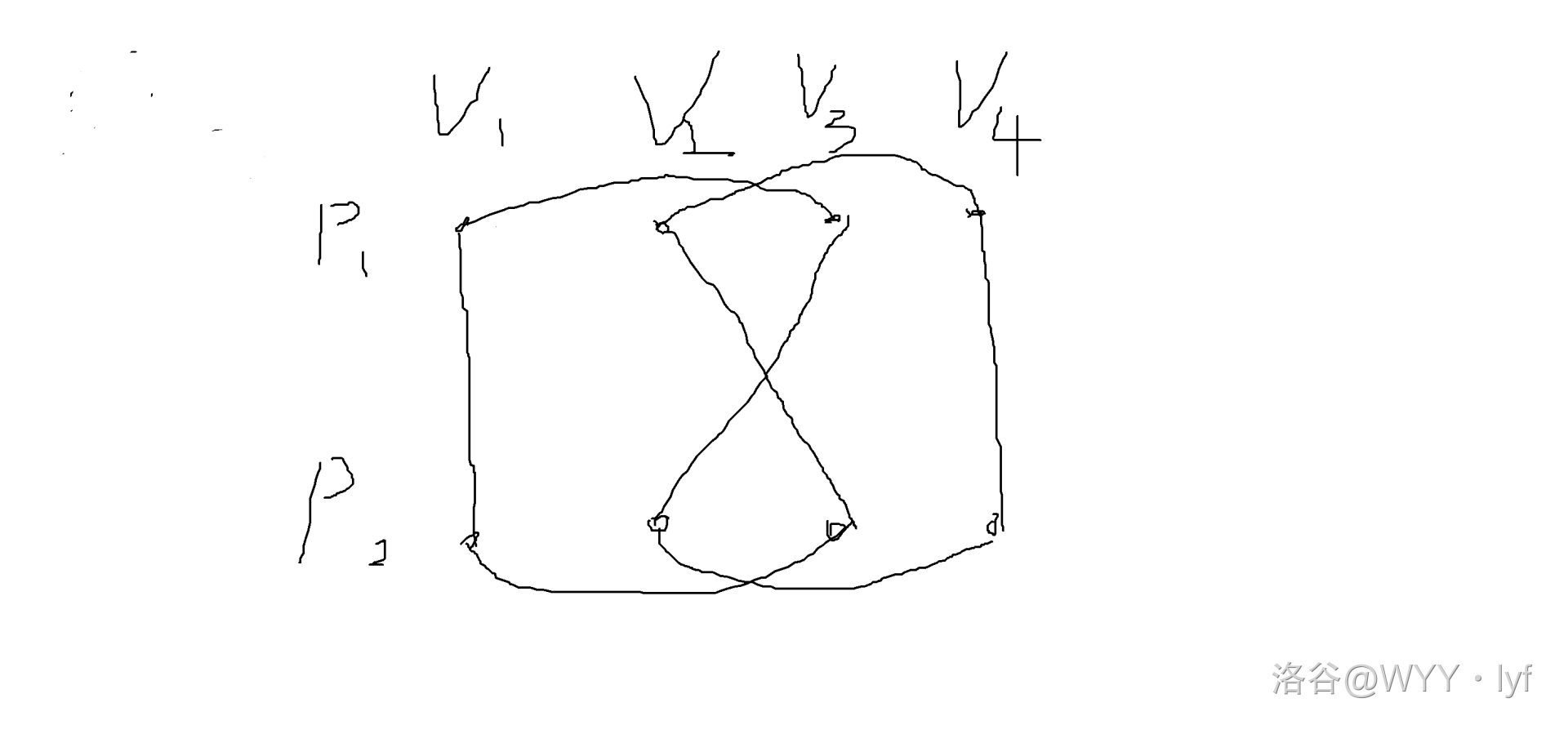
这样你就会发现，你可以从任意位置出发，到达给定的任意位置，那么我们就达到了目的。

具体实现请看代码 ------------------->

【朴实无华的Code】

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1e6 + 5;//数据范围1e6足矣 

int n;
int d, ans;
int f[N>>1];//我们把传送门抽象成点，所以f数组要开2*N 
int p[N][4];//用于存四个传送门的信息 

struct bal {
	int pos;
	int sum;
};
bal t[N];//结构体存点的信息 

int re() {//快读不赘述 
	int x = 0, f = 1;
	char ch = getchar();
	while (ch < '0'||ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while (ch <= '9'&&ch >= '0') {
		x = x*10+ch-'0';
		ch = getchar();
	}
	return x*f;
}

int find(int x) {//这里提一下，优化后的找父亲 
	while(x != f[x])
	x = f[x] = f[f[x]];//路径压缩与找父亲同步，比递归省时 
	return x;
}

void un(int a, int b) {//合并 
	a = find(a);
	b = find(b);
	f[a] = b;
}

int cmp(bal a, bal b) {//按牟尼数进行排序 
	return a.sum < b.sum;
}

signed main() {
	n = re();
	for(int i = 1; i <= n<<1; i++)//注意要n<<1 
		f[i] = i;
	for(int i = 1; i <= n; i++) {
		t[i].pos = i; t[i].sum = re();
		p[i][0] = re(); p[i][1] = re();
		p[i][2] = re(); p[i][3] = re();
		un(p[i][0], p[i][1]);
		un(p[i][2], p[i][3]);//将已经联通的合并，初始化为多个环
	}
	sort(t + 1, t + n + 1, cmp);//cmp
	for(int i = 1; i <= n; i++) {//经典Kruskal，使所有环联通
		d = t[i].pos;
		int x = find(p[d][0]);
		int y = find(p[d][2]);
		if(x != y) {
			f[y] = x;
			ans += t[i].sum;
		}//这里直接跑完n即可，因为我不会优化... 
	}
	printf("%d\n", ans); 
	return 0;//好习惯哦 
}

END

其他一些无关紧要的东西

• 如果您感觉这道题解对您有帮助，请留下您的肯定
• 如果有什么错误的地方，请不要吝啬您的评论
• 还有，目前已知最优解就是本人撒

欢迎大佬们光顾我的博客