自动搬运

查看原文

来自洛谷，原作者为

	Miko35 阿玮你又在打电动喔，去看会书好不好

搬运于2025-08-24 22:30:28，当前版本为作者最后更新于2021-04-07 11:49:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

验题人来水一水题解。

异或，比大小，很容易想到 Trie 树。但是这题插入的是二元组，很难用普通的 01trie 进行维护。

既然是二元组，有一个初步的想法是，将 Trie 开成四叉的，其中令 $ch_{x,i,j}(i,j \in \{ 0,1 \})$ 表示：节点 $x$ 内的二元组 $(x,y)$ 中，$x$ 二进制下一位为 $i$，$y$ 二进制下一位为 $j$ 的二元组集合。也就是说，插入的向量的第 $i$ 位是 $(x,y)$ 取第 $i$ 位形成的二元组。

比如从高到低插入插入二元组 $(1,3)$：

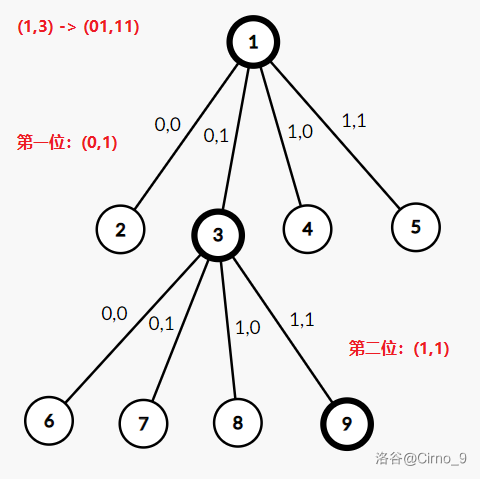
这样就可以像 01trie 一样实现异或比大小，也就是：将 $x \operatorname{xor} a=1,y \operatorname{xor} b=0$ 的节点计入答案，然后分别递归 $x \operatorname{xor} a=y \operatorname{xor} b=0/1$ 的点。

显然这样不是很对，因为每一层要递归两个节点，一次操作总共涉及的节点数到了 $O(M)$ 级别。

观察可知，一个点能被递归下去，当且仅当在这一位 $x \operatorname{xor} a=y \operatorname{xor} b$，而这个可以写成 $x \operatorname{xor} y=a \operatorname{xor} b$，左边只跟 $x,y$ 有关。这样插入时只需要保留两个儿子：下一位 $x \operatorname{xor} y=1$ 和 $=0$ 的，查询时只需要根据 $a \operatorname{xor} b$ 的取值决定往哪边走即可。

依然要在每个节点处记录下一位 $(x,y)=(0/1,0/1)$ 的二元组个数，这样才可以在递归时统计答案。

良心题，代码真心不长。

#include<bits/stdc++.h>
#define g(a) ((a)>>d&1)
long long x,y;
int m,o,c,S[1<<23][2][2],r,h[1<<23][2];
void s(int& r,int d){
	if(~d)S[r?r:r=++c][g(x)][g(y)]+=3-o*2,s(h[r][g(x^y)],d-1);
}
int q(int r,int d){
	return r&&~d?S[r][!g(x)][g(y)]+q(h[r][g(x^y)],d-1):0;
}
int main(){
	std::cin>>m;
	while(m--)std::cin>>o>>x>>y,o^3?s(r,60):void(printf("%d\n",q(r,60)));
}