自动搬运

查看原文

来自洛谷，原作者为

	linch 即得易见平凡，仿照上例显然。留作习题答案略，读者自证不难。 反之亦然同理，推论自然成立。略去过程 Q.E.D.，由上可知证毕。

搬运于2025-08-24 22:30:23，当前版本为作者最后更新于2024-12-15 13:48:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Tips

本题简单版为 P4513。如果您已经完成了那题，可以跳过第一部分。

时间有限，图画的不是特别规整，但还比较清晰，有助于理解。

Solution

Part I 信息维护

本题要求区间修改、区间查询，容易想到要使用线段树。但是线段树直接维护最大子段和不好维护，上传时会遇到困难。我们需要一些辅助信息。

可以尝试从 push_up 函数或分治的角度找出合并时需要的信息。假设我们已经维护出了两个子区间内的需要的信息，按下图讨论：

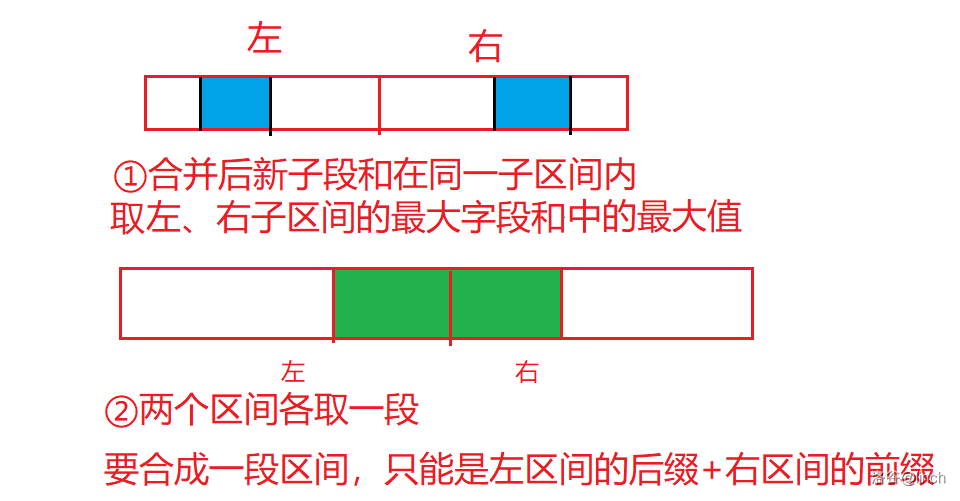
分类讨论，若新子段和没有跨越两个子区间（即只在其中一个区间，如上图情况一，蓝色部分），则此时最大子段和为两区间的最大字段和的较大者。

若跨越了两个区间，此时由左区间后缀和右区间前缀拼接而成（如上图情况二，绿色部分）。既然要求最大，那么应该是左区间最大后缀 $suf_r$ 和右区间最大前缀 $pre_r$。

最终答案为上图两段蓝色和一段绿色中的最大值。可写出式子 $ans=\max\{ans_l,ans_r,suf_l+pre_r\}$。

在上述过程中，我们还使用到了最大前、后缀，也需要进行维护。

以最大前缀为例，如下图：

分类讨论，可能只取左区间一部分，此时合并后最大前缀即为左区间最大前缀 $pre_l$。也有可能跨越了整个左区间，此时最大前缀为左区间和 $sum_l$ 加上右区间最大前缀 $pre_r$。可写出式子 $pre=\max\{pre_l,sum_l+pre_r\}$。

最大后缀同理。但是在过程中使用到了区间和，也需要维护一下。

至此我们完成了信息维护部分。

完成后 push_up 函数代码：

void push_up(int id){
	sum[id]=sum[id<<1]+sum[id<<1|1];
	ans[id]=max({ans[id<<1],ans[id<<1|1],suf[id<<1]+pre[id<<1|1]});
	pre[id]=max(pre[id<<1],sum[id<<1]+pre[id<<1|1]);
	suf[id]=max(suf[id<<1|1],sum[id<<1|1]+suf[id<<1]);
}

Part II 修改

按位或操作不太方便使用懒标记记录，那就无法直接进行区间修改，只能进行单点修改。

但是容易发现按位或有一些性质可以使用。

设 $f(x)$ 为 $x$ 中二进制位 $1$ 的个数。那么每次按位或后，$f(x)$ 只会增大或不变。由于 $-2^{30}\leq a_i,k<2^{30}$，那么这个数最多只有 $30$ 个二进制位。也就是说，最多只有 $30$ 次有效按位或操作（指对其有影响的操作）。

我们可以再维护一下每个区间的按位与和。当一个区间的按位与和值 $p$ 满足 $p \operatorname{and} k=k$ 时，$k$ 中所有为 $1$ 的二进制位在该区间的每一个数中均为 $1$，这样的操作对所有数都没有影响，就不需要递归到这个区间中。

我们已经完成了本题，总时间复杂度 $O(n\log n \log a)$，可以通过本题。

Part III 总结

本题使用了无懒标记的单点修改线段树，需要维护区间和、区间最大前缀、区间最大后缀、区间最大子段和。

主要还是思维，在线段树题目中相对代码难度不高。

Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+10;
long long n,m,a[maxn],ans[maxn],pre[maxn],suf[maxn],sum[maxn],ad[maxn];
void push_up(int id){
	sum[id]=sum[id<<1]+sum[id<<1|1];
	ans[id]=max({ans[id<<1],ans[id<<1|1],suf[id<<1]+pre[id<<1|1]});
	pre[id]=max(pre[id<<1],sum[id<<1]+pre[id<<1|1]);
	suf[id]=max(suf[id<<1|1],sum[id<<1|1]+suf[id<<1]);
	ad[id]=ad[id<<1]&ad[id<<1|1];
}
void build(int l,int r,int id){
	if(l==r){
		ans[id]=pre[id]=suf[id]=max(0ll,a[l]);
		ad[id]=sum[id]=a[l];
		return;
	}
	int mid=l+r>>1;
	build(l,mid,id<<1);
	build(mid+1,r,id<<1|1);
	push_up(id);
}
void update(int l,int r,int s,int t,int id,long long num){
	if(s==t){
		ad[id]|=num;sum[id]|=num;
		ans[id]=pre[id]=suf[id]=max(0ll,sum[id]);
		return;
	}
	int mid=s+t>>1;
	if(l<=mid && ((ad[id<<1] & num) !=num)) update(l,r,s,mid,id<<1,num);
	if(r>mid && ((ad[id<<1|1] & num) !=num)) update(l,r,mid+1,t,id<<1|1,num);
	push_up(id);
}
struct node{
	long long a,p,s,sm;
};
node mg(node xx,node yy){
	node ret;
	ret.sm=xx.sm+yy.sm;
	ret.a=max({xx.a,yy.a,xx.s+yy.p});
	ret.p=max(xx.p,xx.sm+yy.p);
	ret.s=max(yy.s,yy.sm+xx.s);
	return ret;
}
node qry(int l,int r,int s,int t,int id){
	if(s>=l && t<=r){
		return {ans[id],pre[id],suf[id],sum[id]};
	}
	int mid=s+t>>1;
	if(l<=mid && r>mid) return mg(qry(l,r,s,mid,id<<1),qry(l,r,mid+1,t,id<<1|1));
	else if(l<=mid) return qry(l,r,s,mid,id<<1);
	else if(r>mid) return qry(l,r,mid+1,t,id<<1|1);
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	build(1,n,1);
	for(int i=1;i<=m;i++){
		long long op,x,y,z;
		cin>>op>>x>>y;
		if(op==1){
			cout<<qry(x,y,1,n,1).a<<"\n";
		}
		else{
			cin>>z;
			update(x,y,1,n,1,z);
		}
	}
	return 0;
}

AC record