自动搬运

查看原文

来自洛谷，原作者为

	abruce I won't feel lonely, nor will I be sorrowful... not before everything is buried.

搬运于2025-08-24 22:30:15，当前版本为作者最后更新于2021-01-05 21:47:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一个奇异的想法，结果调了我一周多。。。

40pts(1)

二分很好看出来，关键在判定。
如果合法的话，一个数要么被划分进 $a$，要么被划分进 $b$，由此我们可以想用 2-SAT 去判定。这样，也能处理下面的 $u$ 和 $v$ 不在同一个可重集的问题。
对于那两个基本条件，我们可以对于每一个 $j<i\ \text{and}\ v_j\le v_i-k$ 的 $j$ 都连一条 $j$ 选了 $a,i$ 就不能选 $a$ 的边。同理对于每一个 $j<i\ \text{and}\ v_j\ge v_i+k$ 的 $j$ 都连一条 $j$ 选了 $b,i$ 就不能选 $b$ 的边。
我们现在可以暴力连边，虽然最多 $n^2$ 条边，但前面 40 分的数据还是可以通过的。

40pts(2)

再看 $m=0$ 的情况，$a$ 中的每个数保证了 $a_i<\min {a_j}+k$，$b$ 中的每个数保证了 $b_i>\max {b_j}-k$。
现在我们记录 $a$ 中最小值和 $b$ 中最大值，每次来一个数看能不能放进去，放哪一个更优一些，然后更新。
如果有一个放不进去，那就说明非法。（口胡算法）

100pts

显然这两个算法不能直接结合再一起，我们考虑优化其中一个算法。我们发现那个贪心算法比较难处理 $u$ 和 $v$ 之间不能连边，所以我们考虑优化第一个算法的连边过程。
这相当于实在 2-SAT 中向 $j<i\ \text{and}\ v_j\le v_i-k$ 和 $j<i\ \text{and}\ v_j\ge v_i+k$ 分别连边。这时我们可以使用主席树或者树状数组（orz ー念之间、、）优化建图。
假设将权值离散化后，我们将其建成了一个树状数组。

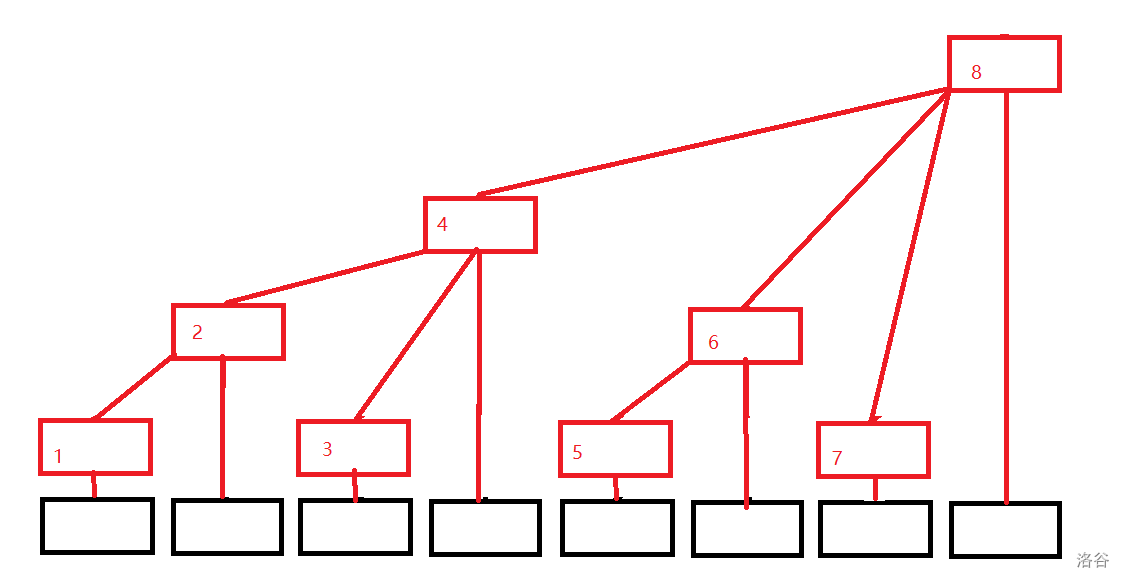
我们接下来假设往入树中插入了节点1和2。

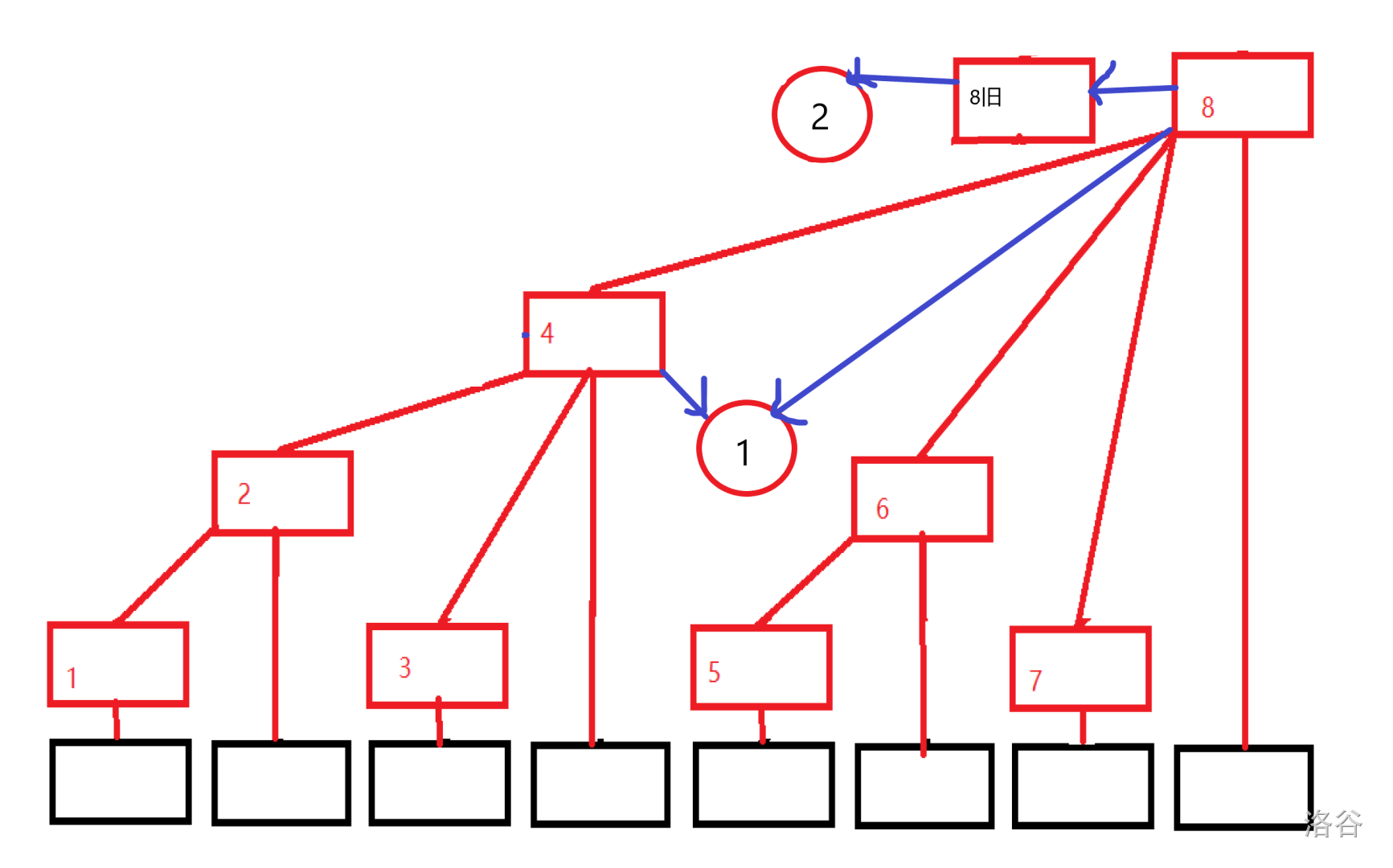
通过当前树状数组节点指向上一个的旧节点，我们可以通过这样得到以前的信息，从而优化建图。我们进行连边时，每次连向当前的树状数组节点就可以得到相应的边。
注意细节。

#include<bits/stdc++.h>
using namespace std;
char __buf[1<<12],*__p1,*__p2;
//#define getchar() (__p1==__p2?(__p2=__buf+fread(__p1=__buf,1,1<<12,stdin),__p1==__p2?EOF:*__p1++):*__p1++)
inline int read() {
	int __x=0,__f=1;
	char __c=getchar();
	while(__c<'0'||__c>'9') {
		if(__c=='-')__f=-1;
		__c=getchar();
	}
	while(__c>='0'&&__c<='9') {
		__x=__x*10+__c-'0';
		__c=getchar();
	}
	return __x*__f;
}
char __F[200];
inline void write(int __x) {
	if(__x<0) {
		putchar('-');
		__x=-__x;
	}
	if(__x>=10)write(__x/10);
	putchar(__x%10+'0');
}
const int maxn=2e4+5,maxm=2e6+5;
struct edge {
	int next,to;
} e[maxm*4],w[maxn*8];
int a[maxn],g[maxn*2],book[maxn],bc,cnt,cnt2,h[maxm],dfn[maxm],low[maxm],col[maxm],color,n,m,s1[maxn][2],s2[maxn][2],tot,ans,ind,midd;
bool inst[maxm];
stack<int> s;
inline void addedge(int x,int y) {
	e[++cnt].next=h[x];
	e[cnt].to=y;
	h[x]=cnt;
}
inline void addedge2(int x,int y) {
	w[++cnt2].next=g[x];
	w[cnt2].to=y;
	g[x]=cnt2;
}
inline int lowbit(int x) {
	return x&(-x);
}
inline void add(int x,int y,int pd) {
//s1表示入树，s2表示出树。我们在向里面添加的时候，入树往它连边；它往出树连边。
	for(register int i=x; i<=bc; i+=lowbit(i)) {
		tot++;
		if(s1[i][pd]) {
			addedge(tot,s1[i][pd]);
			addedge(tot+1,s1[i][pd]+1);//往以前取到这个值的点连边
		}
		s1[i][pd]=tot;
		addedge(tot,y);
		addedge(tot+1,y+1);//把这个点挂在入树下面
		tot+=2;
		if(s2[i][pd]) {
			addedge(s2[i][pd],tot);//同理
			addedge(s2[i][pd]+1,tot+1);
		}
		s2[i][pd]=tot;
		addedge(y,tot);
		addedge(y+1,tot+1);
		tot++;
	}
}
inline void link(int x,int y,int pd) {
	int w=pd^1;
	for(register int i=x; i; i-=lowbit(i)) {
		if(s1[i][pd])addedge(y+pd,s1[i][pd]+w);//向对面连边
		if(s2[i][pd])addedge(s2[i][pd]+pd,y+w);
	}
}
inline void tarjan(int u) {
	s.push(u);
	inst[u]=1;
	dfn[u]=low[u]=++ind;
	for(register int i=h[u]; i; i=e[i].next) {
		int j=e[i].to;
		if(!dfn[j]) {
			tarjan(j);
			low[u]=min(low[u],low[j]);
		} else if(inst[j]) {
			low[u]=min(low[u],dfn[j]);
		}
	}
	if(u<=n*2) {//注意这里可能造成的数组越界
		for(register int i=g[u]; i; i=w[i].next) {
			int j=w[i].to;
			if(!dfn[j]) {
				tarjan(j);
				low[u]=min(low[u],low[j]);
			} else if(inst[j]) {
				low[u]=min(low[u],dfn[j]);
			}
		}
	}
	if(dfn[u]==low[u]) {
		color++;
		int k;
		do {
			k=s.top();
			s.pop();
			inst[k]=0;
			col[k]=color;
		} while(k!=u);
	}
}
inline bool check(int mid) {
	memset(h,0,sizeof(h));
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	memset(col,0,sizeof(col));
	memset(s1,0,sizeof(s1));
	memset(s2,0,sizeof(s2));
	cnt=ind=color=0;
	while(!s.empty()) {
		s.pop();
	}
	tot=2*n;
	for(register int i=1; i<=n; i++) {
		int p=upper_bound(book+1,book+bc+1,a[i]-mid)-book-1;//注意是upper_bound
		if(p)link(p,i*2-1,0);
		p=lower_bound(book+1,book+bc+2,a[i]+mid)-book;//这里右边界是bc+1
		if(p<=bc)link(bc-p+1,i*2-1,1);
		p=lower_bound(book+1,book+bc+1,a[i])-book;
		add(p,i*2-1,0);
		add(bc-p+1,i*2-1,1);
	}
	for(register int i=1; i<=2*n; i++) {
		if(!dfn[i]) {
			tarjan(i);
		}
	}
	for(register int i=1; i<=n; i++) {
		if(col[i*2-1]==col[i*2]) {
			return 0;
		}
	}
	return 1;
}
int main() {
	int x,y;
	n=read(),m=read();
	for(register int i=1; i<=n; i++) {
		a[i]=read();
		book[++bc]=a[i];
	}
	sort(book+1,book+bc+1);
	bc=unique(book+1,book+bc+1)-book-1;//离散化
	book[bc+1]=book[bc]+1;//注意往比它大的连边时所取的值能不能取到最后一个。
	for(register int i=1; i<=m; i++) {
		x=read(),y=read();
		addedge2(x*2-1,y*2);
		addedge2(x*2,y*2-1);
		addedge2(y*2,x*2-1);
		addedge2(y*2-1,x*2);
	}
	for(register int i=1; i<=2*n; i++) {
		if(!dfn[i]) {
			tarjan(i);
		}
	}
	for(register int i=1; i<=n; i++) {
		if(col[i*2-1]==col[i*2]) {
			puts("-1");
			return 0;
		}
	}
	int l=1,r=1e9;
	while(l<=r) {
		int mid=(l+r)/2;
		if(check(mid)) {
			ans=mid;
			r=mid-1;
		} else {
			l=mid+1;
		}
	}
	write(ans);
	return 0;
}