自动搬运

查看原文

来自洛谷，原作者为

	Mine_King 欢迎访问个人博客：caijimk.netlify.app

搬运于2025-08-24 22:30:11，当前版本为作者最后更新于2021-03-28 20:49:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题其实挺好想的，只需要画两个图：

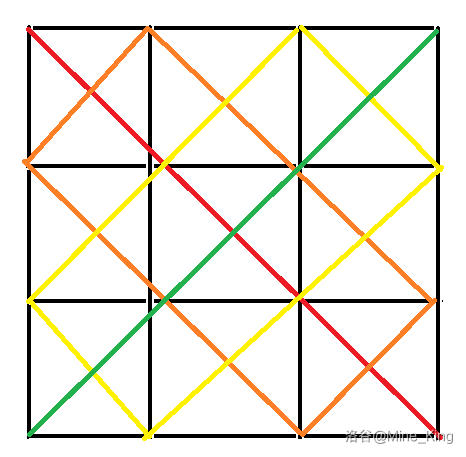
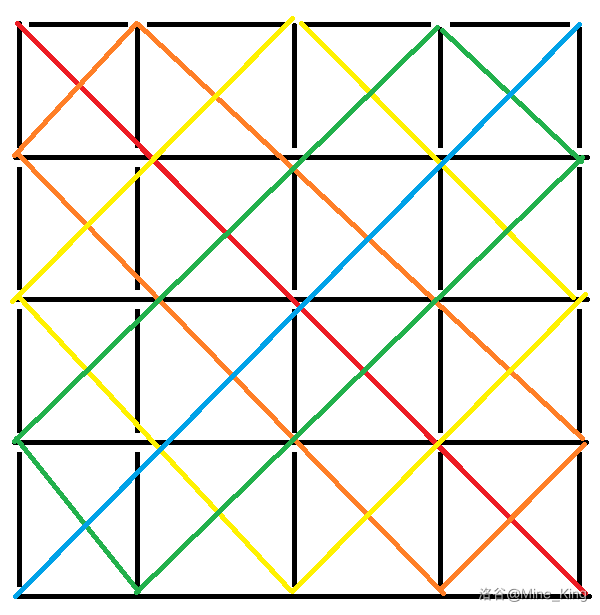
这两张分别是 $n=4$ 和 $n=5$ 时(因为可以猜想路径和某些东西的奇偶性有关，所以挑两张 $n$ 的奇偶性不同的图)的网格和吃豆人行走的路径图（彩色的是路径，黑线的焦点是有豆子的点）

观察这两张图可以得到如下性质：

• 共有 $n$ 条路径。
• 每条路径都是一个回路或对角线。
• 在网格图的四条边的任意一条边上都会同时出现这 $n$ 条路径，我们以最上面的一条边为标准，以路径在这条边上出现时的纵坐标来标记这条路径，如红线的编号为 $1$
• 若编号为 $x,y$ 的两条路径满足 $y-x$ 是偶数，则这两条路径存在共同经过的点，否则不存在共同经过点。
• 若 $u,v$ 两条路径有共同经过的点，则：
  • 如果 $u,v$ 是两条对角线，则有一个共同经过的点，且该点为网格的中心。
  • 如果是一条对角线和一条回路，那么有两个焦点。
  • 如果是两条回路，那么有四个焦点。
• 若 $u,v$ 两条路径有共同经过的点且不是两条对角线，则共同经过的点关于第一条对角线对称，即每对共同经过的点的横纵坐标相反。

由于 $n$ 比较小，我们可以 $O(n^2)$ 预处理出每条路径能吃的豆子数，$O(n^2)$ 来枚举吃豆人走的路径。
现在唯一的问题就是要求出我们选的两条路径的共同经过的点上的豆子数之和。

这里我们需要进行分类讨论。
设我们现在选的路径编号为 $u,v$，且 $v>u$，共同经过的点上的豆子数之和为 $ans$，坐标 $(i,j)$ 上的豆子数为 $a_{i,j}$，则：

• 若 $v-u$ 是奇数，则 $ans=0$，否则
  • 若 $u=1$ 且 $v=n$（即两条对角线），则 $ans=a_{(n+1)/2,(n+1)/2}$。
  • 若 $u=1$ 且 $v \not= n$（即回路和第一条对角线），则 $ans=a_{(v+1)/2,(v+1)/2}+a_{(2n-y+1)/2,(2n-y+1)/2}$。
  • 若 $u \not= 1$ 且 $v=n$（即回路和第二条对角线），则 $ans=a_{(n-x)/2+1,(n+x)/2}+a_{(n+x)/2,(n-x)/2+1}$。
  • 若 $u \not= 1$ 且 $v \not= n$（即两条回路），则 $ans=a_{(x+y)/2,(y-x)/2+1}+a_{(y-x)/2+1,(x+y)/2}+a_{n-(y-x)/2,n-(x+y)/2+1}+a_{n-(x+y)/2+1,n-(y-x)/2}$。

这几点也可以通过找规律和推式子得到。

于是就可以快快乐乐地写出代码啦~

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,a[1005][1005];
int ans,b[1005];//b[i]是第i条对角线的豆子数量
const int gx[4]={1,1,-1,-1};
const int gy[4]={-1,1,1,-1};
int repeat(int x,int y)//这里判共同经过的点的豆子数量
{
	if((y-x)%2) return 0;//无共同经过的点
	if(x==1&&y==n) return a[(n+1)/2][(n+1)/2];//两条对角线
	if(x==1) return a[(y+1)/2][(y+1)/2]+a[(2*n-y+1)/2][(2*n-y+1)/2];//第一条对角线和回路
	if(y==n) return a[(n-x)/2+1][(n+x)/2]+a[(n+x)/2][(n-x)/2+1];//第二条对角线和回路
	return a[(x+y)/2][(y-x)/2+1]+a[(y-x)/2+1][(x+y)/2]+a[n-(y-x)/2][n-(x+y)/2+1]+a[n-(x+y)/2+1][n-(y-x)/2];//两条回路
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++) scanf("%d",&a[i][j]);
	if(n==1){printf("%d\n",a[1][1]);return 0;}//特判n=1的情况，否则下面的计算路径中的豆子数量会挂掉
	for(int i=1;i<=n;i++)
	{
		int x=1,y=i,d=0;
		do
		{
			b[i]+=a[x][y];
			if(d==0&&y==1) d++;
			else if(d==1&&x==n) d++;
			else if(d==2&&y==n) d++;
			else if(d==3&&x==1) d++;
			d%=4;
            //这里是发生镜面反射时的方向改变
			x=x+gx[d],y=y+gy[d];
		}
		while(x!=1&&(x!=n||y!=n)&&(x!=n||y!=1));//这里是计算路径上的豆子数量
		if(i==1) b[i]+=a[n][n];
		if(i==n) b[i]+=a[n][1];
        //这两条特判对角线
	}
	for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++)
			ans=max(ans,b[i]+b[j]-repeat(i,j));//枚举选的路径
	printf("%d\n",ans);
	return 0;
}