自动搬运

查看原文

来自洛谷，原作者为

	songhongyi 懒

搬运于2025-08-24 22:30:07，当前版本为作者最后更新于2023-07-08 21:24:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

简单数数题。

题目所求的等腰直角三角形有四种方向，不难发现本质相同。考虑只求一种然后旋转网格重复四次。

先说旋转网格，以左旋 $\frac \pi 2$ 为例，发现相当于第 $i$ 行倒序放置在了第 $i$ 列，故可通过下式表述这个过程。

下面讲求答案。不妨设我们求右下角为直角的情况。

发现所求的三角形只由两个量决定：右下角坐标与边长。

注意到一个事实：以某个点为顶点的三角形数量等于最大的三角形边长减 1。

证明如下：

• 显然可以取到的边长连续，设为 $2,3,\cdots n$（题目强调了 $1$ 不行）；
• 则最大变长为 $n$ ，个数为 $n-1$。

那么问题转化为：求每个点为顶点的三角形边长最大值。

考虑 DP，设 $f_{i,j}$ 为 $(i,j)$ 为顶点的答案。

朴素为 $1$ 的情况显然当且仅当 $(i-1,j)$ 或 $(i,j-1)$ 的颜色与 $(i,j)$ 不同，下面默认相同。

下面引出本题的重要结论：$f_{i,j}= \min (f_{i-1,j},f_{i,j-1})+1$

从下图中不难看出，若右侧值更小，说明最外侧有非同色位置，这非法；若右侧值更大，则最外圈都同色，左侧的值也能扩大。

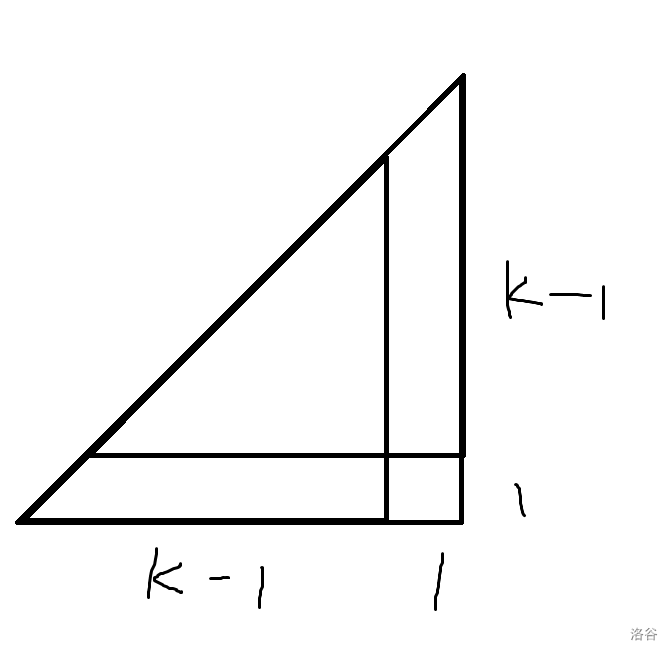
因此按照上式转移即可，复杂度 $O(n^2)$。