自动搬运

查看原文

来自洛谷，原作者为

	约瑟夫用脑玩 AFO

搬运于2025-08-24 22:29:41，当前版本为作者最后更新于2021-05-03 16:39:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

换一种方式来解释这道题的贪心可能更好理解一点。

首先我们得知道新图只与函数 $f$ 的值有关，而由于我们可以在一条边上来回横跳，所以 $f$ 是否有值取决于奇/偶最短路的长度，那么我们用 $O(n)$ BFS 出最短路即可。

注意特判一下每个点只有奇数路径或偶数路径，即这是个二分图，那么直接用原图的最短路树就可以表示了。

否则，每个点都会有奇数和偶数路径，设一个点的奇最短路和偶最短路二元组为 $(x,y)$。

由于顺序并没有关系，且为了好看方便，我们取 $x$ 为奇偶中较短的最短路，$y$ 为较长的，即 $x<y$。

那么考虑导致 $(x,y)$ 的方式：

• 有另一个点奇偶最短路分别为 $(x-1,y-1)$ ，并连了一条边。

• 有两个点分别为① $(x-1,y+1)$ 和② $(x+1,y-1)$ ，都连了一条边。注意当 $x+1=y$ 时，有 $(x+1,y-1)=(y-1,x+1)=(x,y)$

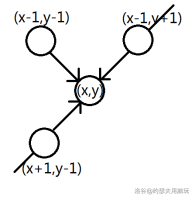
解释一下：第二个方式中①的第一维保证较小最短路为 $x$，②第二维保证了较大最短路为 $y$，而他们的其他维由于与 $(x,y)$ 的点有直接连边故最大都只能 $+1$。

第一种方式只用一条边显然血赚，但可能没有 $(x-1,y-1)$ 的点，此时就只能用第二种方式。

所以才出现了如下的贪心方法：

• 按先 $x+y$ 为第一维，再 $x$ 为第二维依次考虑。（下图中纵坐标为倒着的 $x+y$，横坐标为倒着的 $x$，故先从上到下，再从右到左依次考虑，也就是把上图往右掰了一点）

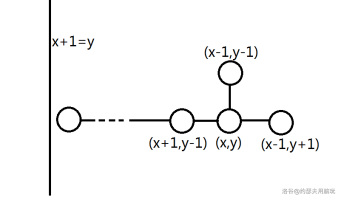
• 如果右边 $(x-1,y+1)$ 没有第二种方式的需求传过来，那么 $(x,y)$ 直接选第一种方式。

  否则 $(x,y)$ 的一部分点用于满足其需求，于是还会有需求往左 $(x+1,y-1)$ 传，如果 $(x,y)$ 点数有多余的就还是用第一种方式。

  最后我们会传到 $x+1=y$ 的边界，此时就相当于同类连边不再传了。

  这样看的话，就是将必须用第二种方式的边一直往左传，传到边界用每个点 $\frac{1}{2}$ 的代价消掉，而传时还有 $1$ 的代价，故将本来用 $2$ 的代价减小为 $1.5$ 的代价。

  注意到 $1.5<1$，故有多余不用传时尽量还是用第一种方式。

和其他题解最后的做法都一样，但思路可能会好理解点qwq。

估计没人看的代码

Upd：修改了一点小锅，以前是对的表述就没改了。（虽然读着有点奇怪）