自动搬运

查看原文

来自洛谷，原作者为

	遮云壑 QQ:2430364453ฏ๎็็็็ฏ้้้้้้้้้้้้้้้้้้้้้้้้้้้้้้้้้้ด้้้้้้้็้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้

搬运于2025-08-24 22:29:34，当前版本为作者最后更新于2021-11-03 16:52:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Description

出门左转

教练原话：JOI Final=日本的NOIP？？（大雾）

Solution

大体思路：建虚点+最短路

1. 为什么要建虚点？

当你在一个点决策下一步时，决策会有很多种情况，虚点的作用就是让我们考虑到所有的这些情况。

2. 如何建立虚点？敲黑板敲黑板

首先考虑会有几种情况

• 该颜色在当前点只有一种，花费为0
• 该颜色在当前点有多种，可以改它自身，也可以该它的其他所有相同颜色的小伙们
• 从一个多颜色的点进来，并且选择这一颜色的点出去，同时出去的时候选择改变其他所有同色边的方案

这样说，十分空洞，看不懂先跳吧，后面还会讲。

插播一个性质：我们对边改颜色可以做到不对后来产生任何影响。

原因很显然，一共有 $M$ 种颜色，只要我们想，是可以做到每一条边的颜色各不相同的。

放个图，更好理解。（为了表示颜色，只有手绘了，手残勿喷TAT）

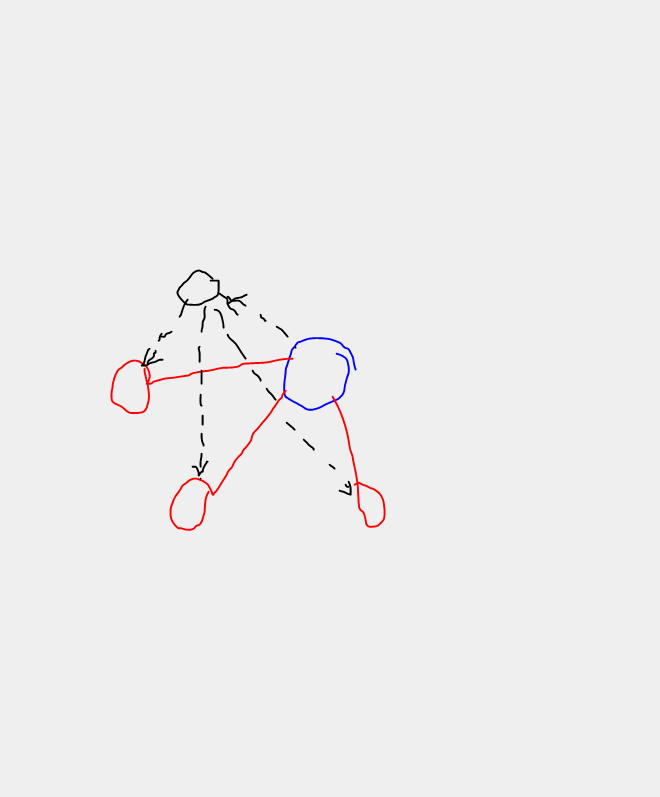
蓝色是你现在在的点，红色是几个相同颜色的点，黑色是所谓的虚点。

声明一下，这题虚点连的边都是有向边，因为权值会不同。

1. 建虚点，每一种颜色建一个虚点
2. 当前点向虚点连边（蓝->黑），权值为0
3. 虚点向出去的点连边（黑->红），权值为其他所有同色的边的权值之和
4. 出去的点向虚点连边（红->黑），权值为0

解释：

走2，3两种边，实现了改变其他所有同色边的情况。

走4，3两种边，（4进3出）实现了刚才说的乱七八糟的情况，这里细讲一下。（这非常重要，个人认为这是本题最难的一部分了）

现在我们在一个红点，要进蓝点，并且出来的又是红点，出来的时候选择改变其他所有红边。既然出来的时候改变其他所有的红边，那么进来的那条边肯定也改掉了，可以改成一个进去不需要任何花费的边，出来的时候改变其他红边的权值，所以我们直接以0的花费走到虚点，在以该所有红边的花费走出来，就可以了。

好了，虚点建完了，跑dij吧。

code

#include<bits/stdc++.h>
#define N 1000010
#define int long long
using namespace std;
inline void read(int& x)
{
	x=0;int y=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	x=x*y;
}
int n,m;
struct Node{
	int to,nxt,w,col;
}e[N<<1];
int cnt,head[N];
inline void add(int u,int v,int col,int w)
{
	e[++cnt].col=col;e[cnt].nxt=head[u],e[cnt].to=v,e[cnt].w=w;
	head[u]=cnt;
}
int vis[N],num[N],sum[N],rt[N],tot,d[N];
struct node{
	int dis,id;
	bool operator<(const node& x)const{return dis>x.dis;}
	node(){}
	node(int d_,int id_){dis=d_,id=id_;}
};
priority_queue<node> q;
inline void dij()
{
	memset(d,0x3f,sizeof(d));
	d[1]=0;
	q.push(node(d[1],1));
	while(!q.empty())
	{
		int x=q.top().id;q.pop();
		if(vis[x])continue;vis[x]=1;
		for(int i=head[x];i;i=e[i].nxt)
		{
			int y=e[i].to,w=e[i].w;
			if(d[y]>d[x]+w)
			{
				d[y]=d[x]+w;
				q.push(node(d[y],y));
			}
		}
	}
}
signed main(){
//	freopen("robot.in","r",stdin);
//	freopen("robot.out","w",stdout);
	read(n),read(m);
	for(int i=1;i<=m;i++)
	{
		int x,y,z,zz;
		read(x),read(y),read(z),read(zz);
		add(x,y,z,zz),add(y,x,z,zz);
	}
	tot=n;
//-------------------重点分割线--------------------------- 
	//这一段是关于建虚点的 
	for(int x=1;x<=n;x++)
	{
		for(int i=head[x];i;i=e[i].nxt)
		{
			if(!e[i].col)continue;
			sum[e[i].col]+=e[i].w; 
			num[e[i].col]++;
			//sum表示同色点的权值和，num表示该颜色点有几个 
		}
		for(int i=head[x];i;i=e[i].nxt)
		{
			int y=e[i].to;
			if(!e[i].col)continue;
			if(num[e[i].col]==1)e[i].w=0;//仅一个，花费为0 
			else 
			{
				if(!rt[e[i].col])
				//2类边，蓝->黑 
				//rt记录了每一种颜色的虚点编号 
				{
					rt[e[i].col]=++tot;
					add(x,tot,0,0);
				}
				add(rt[e[i].col],e[i].to,0,sum[e[i].col]-e[i].w);
				//3类边，黑->红，权值为sum[e[i].col]-e[i].w 
				add(e[i].to,rt[e[i].col],0,0);
				//4类边，红->黑，权值为0 
			}
		}
		for(int i=head[x];i;i=e[i].nxt) 
		{
			rt[e[i].col]=sum[e[i].col]=num[e[i].col]=0;
		}
		//别忘了清空数组 
		//由于一个点的度数不会太大，所以直接改会比memset快一点 
	}
//-------------------重点分割线--------------------------- 
	dij();
	if(d[n]==0x3f3f3f3f3f3f3f3f)printf("-1\n");
	else printf("%lld\n",d[n]);
	return 0;
}