自动搬运

查看原文

来自洛谷，原作者为

	lupengheyyds 今日长缨在手，何时缚住苍龙？

搬运于2025-08-24 22:29:30，当前版本为作者最后更新于2023-07-24 12:01:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

原题连接

背景

其他的题解对这道题的做法已经有了大概的讲解，但是对于正解的思路与细节处理说得云里雾里，所以说我将对正解的思路及具体细节作诠释，不再赘述部分分数的解法。

分析

初步转化

看见区间加减，便不由得想到差分，于是建立一个差分数组 $d[i]=a[i]-a[i-1]$ ，这样每次就只需要在两处单点修改。

接着分析，一个区间真正能作出贡献的只有最大值与最小值，也就是说，当我们已经得到一段的极大值与极小值的时候，便应该直接划分，而非继续将其他的数纳入这个区间，最终使得整个划分出来的区间单调不下降或单调不上升。转化为数学语言就是：对于所有划分的区间 $[l,r]$ ，满足 $a[l]\le a[l+1]\le \cdots\le [r]$ 或者 $a[l]\ge a[l+1]\ge \cdots\ge a[r]$ ，接着将其转化为上文的差分思路也就是要满足 $d[l+1],d[l+2],\cdots,d[r]$同号（根据定义，$0$ 应该与任何数同号）。这样的话每个区间最后的值就应该是 $\sum\limits_{i=l+1}^r\left|d[i]\right|$ 。根据这个式子，我们可以发现，因为题目要求最大值，我们就应该尽量少的剔除差分值，非要减也要减去绝对值较小的差分值。

根据前面的分析，现在就需要我们单点修改，区间查询。那不就是线段树吗？于是我们可以尝试从线段树的角度考虑如何合并两个区间。

线段树分析

假设有这样一个区间（下面表示原数组，上面表示差分数组）：

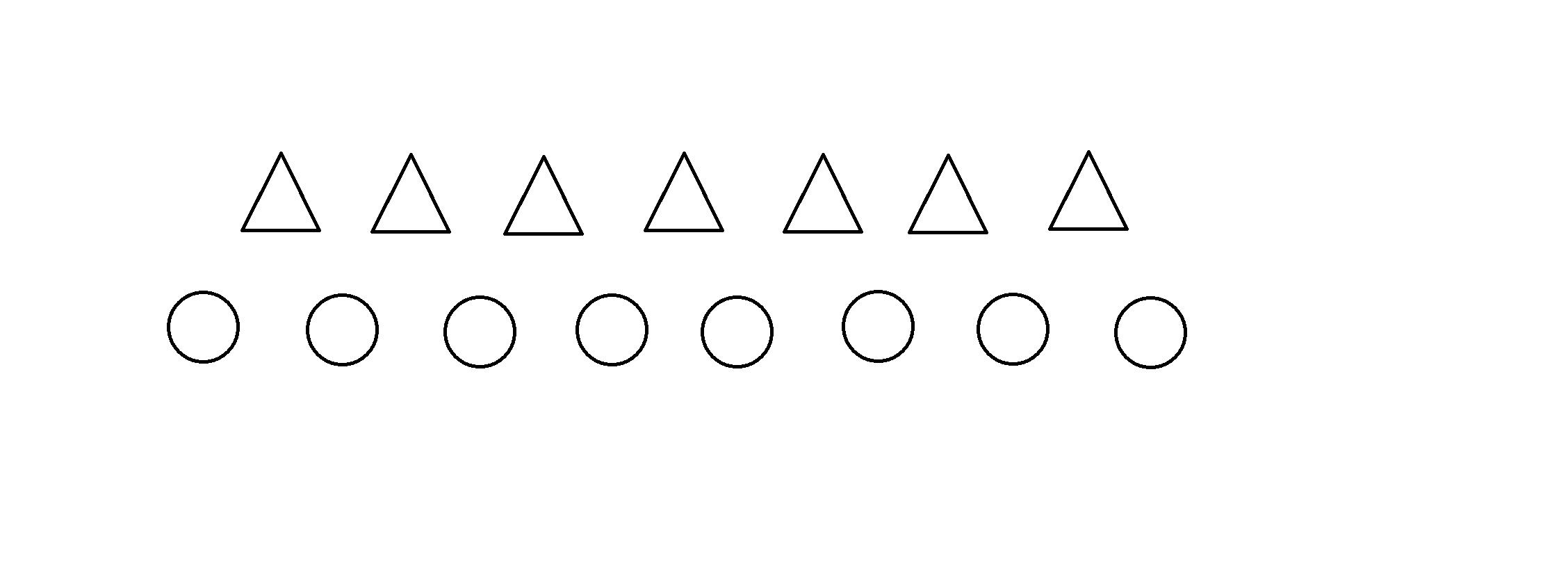
如果在差分线段树上的话，就会被分成这样两个区间：

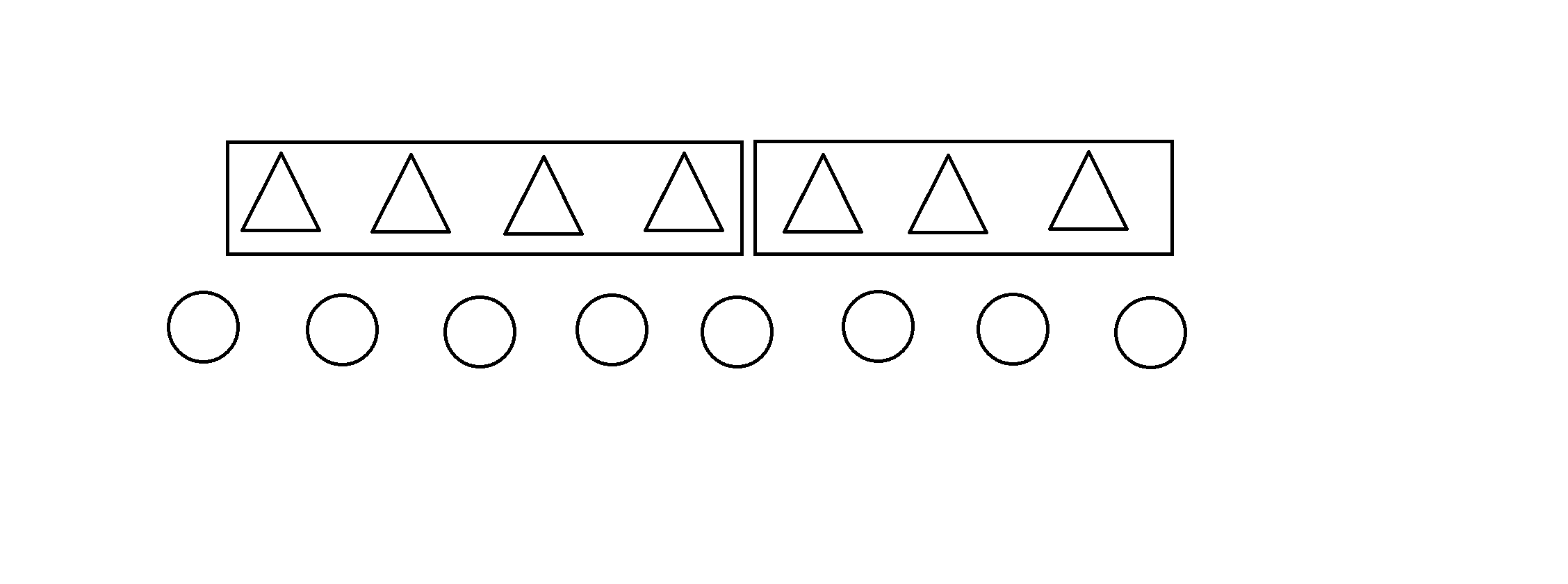
那么对应反映在原数组上就是这样：

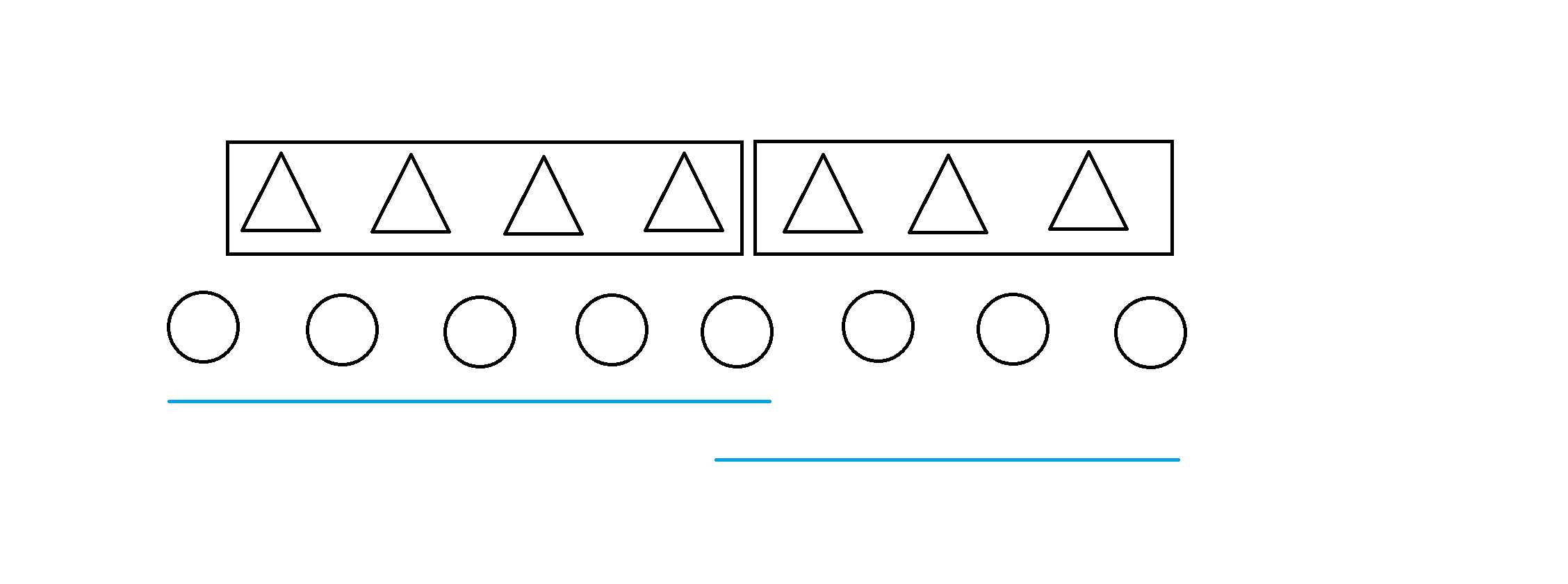
如果两个差分区间符合上述的“初步转换”中的条件的话就可以直接累加，合并成一个区间（过于简单，没有画出）。

但如果两个差分区间不符合条件也就是需要必须分开的时候，就会有一下两种情况：

• 分给左边

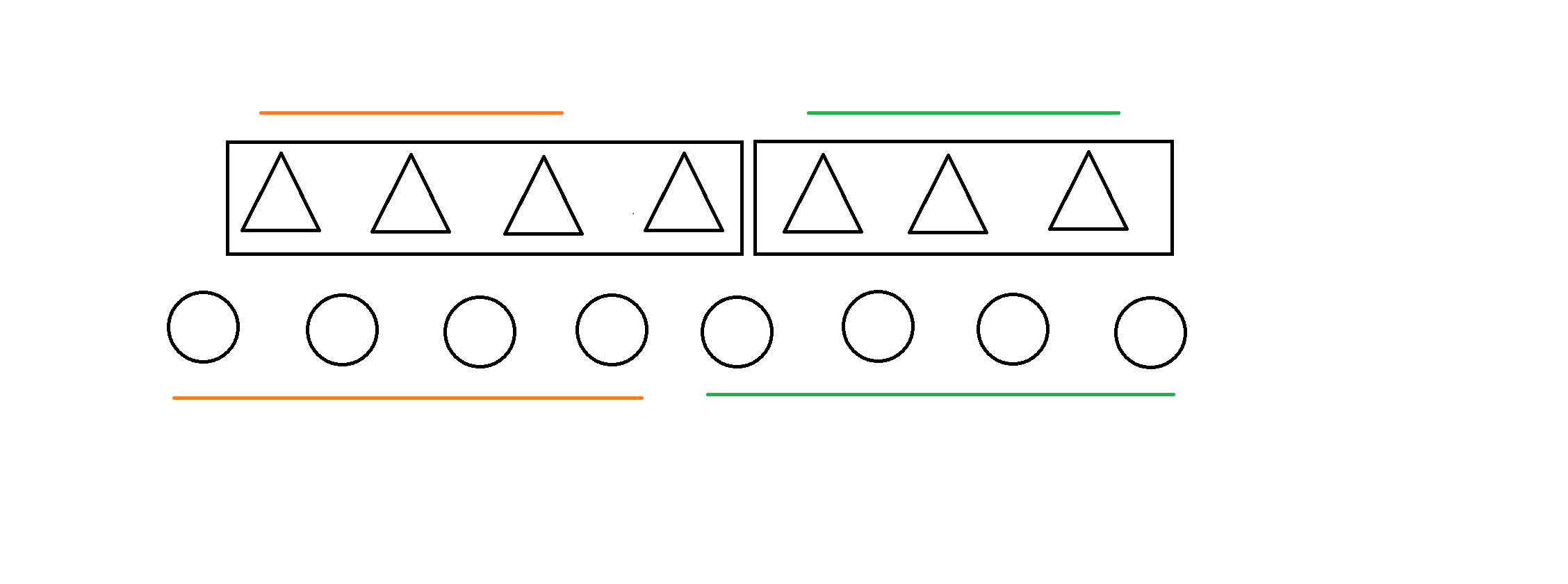
• 分给右边

这是我们就会发现，对于差分区间，其左右两边的值可能选或不选，那么在处理线段树的时候，我们就应该对应存上左右两端选或不选的情况。

最后再输出整个区间，由于整个区间的左右两端选了的答案一定比不选优（多考虑了两个值），所以直接输出两端都选的情况就行，根本不用作比较。

对了，记得开 $\text{long long}$

如果还没有理解，就可以看代码。

代码

#include<bits/stdc++.h>
#define int long long//记得开long long 
using namespace std;
const int szl=8e5+5;
int sgt[szl][2][2];//第一维是线段树节点编号，第二位表示左端点状态，第三位表示由端点状态，0表示不选，1表示选 
int a[szl],d[szl],root=1;
void Updata(int p,int mid){
	for(int i=0;i<=1;i++)
		for(int j=0;j<=1;j++)
			if(d[mid]*d[mid+1]>=0)sgt[p][i][j]=sgt[p<<1][i][1]+sgt[p<<1|1][1][j];//可以合并成一个区间 
			else sgt[p][i][j]=max(sgt[p<<1][i][0]+sgt[p<<1|1][1][j],sgt[p<<1][i][1]+sgt[p<<1|1][0][j]); //不能合并成一个区间 
	return;
}
void Add(int p,int l,int r,int pos){
	if(l==r){
		sgt[p][1][1]=abs(d[l]);
		return;
	}
	int mid=l+r>>1;
	if(pos<=mid)Add(p<<1,l,mid,pos);
	else Add(p<<1|1,mid+1,r,pos);
	Updata(p,mid);
	return;
}

signed main(){
	int n,q;cin>>n>>q;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		d[i]=a[i]-a[i-1];
		if(i==1)continue;
		Add(root,2,n,i);
		//也可以写在外面O(N)建树，但这样写慢却简单，少些一个函数，反正不会超时，减少错误率 
		//注意：差分数组从2到n的区间才有效 。 
	} 
	while(q--){
		int l,r,x;cin>>l>>r>>x;
		if(l>1){
			d[l]+=x;
			Add(root,2,n,l);
		}
		if(r<n){
			d[r+1]-=x;
			Add(root,2,n,r+1);
		}
		cout<<sgt[root][1][1]<<endl;//最后直接输出，不用比较左右端点不选的情况 
	}
	return 0;
}