自动搬运

查看原文

来自洛谷，原作者为

	入户功夫 **

搬运于2025-08-24 22:29:29，当前版本为作者最后更新于2021-10-28 21:01:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

注意到对于每一个山谷，都在上方有一条线段内的位置可以照亮它。

首先不考虑山之间互相有遮挡的情况（subtask 1）。利用初中知识可以很容易算出来对于每个山谷，上方能够照亮它的线段的左右端点。然后就变成了经典的区间覆盖问题：

给定若干线段，用最少的点将其覆盖使得每条线段上至少有一个点。

区间的右端点作为第一关键字从小到大，左端点作为第二关键字从大到小排序。如果再不覆盖就来不及了，盖一个点。

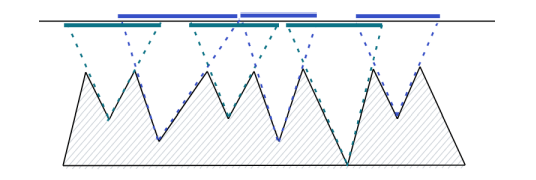
接下来考虑有相互遮挡的情况

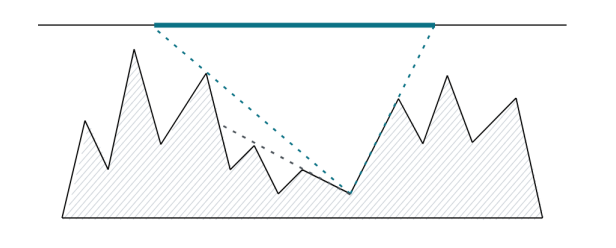
很显然的，左面能遮挡住一个山谷的点一定是它及左侧所有点构成的上凸包的倒数第二个（它本身是倒数第一个）。

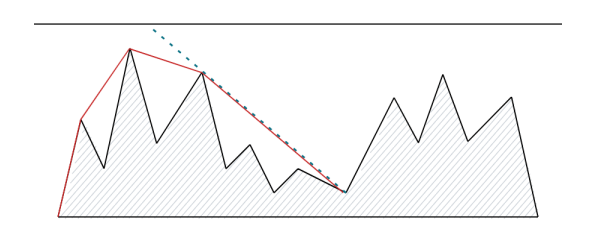
用单调栈 $O(n)$ 维护凸包，就能找到每个山谷对应线段的左端点。再倒着跑一遍就能找到右端点。接下来做线段覆盖。

时间复杂度瓶颈在于线段的排序，$O(n logn)$。

#include<bits/stdc++.h>
using namespace std;
int n;double h;
double x[1000006],y[1000006];
int anss=0;

int stck[1000006],top;
double l[1000006],r[1000006];
inline double slope(int j,int k)
{
	return (y[j]-y[k])/(x[j]-x[k]);
}
inline void init()
{
	stck[top=1]=1;
	for(int i=2;i<=n;i++)
	{
		while(top>1&&slope(stck[top],stck[top-1])<slope(i,stck[top])) top--;
		if(i%2) l[i]=x[stck[top]]-(x[i]-x[stck[top]])/(y[stck[top]]-y[i])*(h-y[stck[top]]);
		stck[++top]=i;
	}
	stck[top=1]=n;
	for(int i=n-1;i;i--)
	{
		while(top>1&&slope(stck[top-1],stck[top])>slope(stck[top],i)) top--;
		if(i%2) r[i]=x[stck[top]]+(x[stck[top]]-x[i])/(y[stck[top]]-y[i])*(h-y[stck[top]]);
		stck[++top]=i;
	}
}

struct nod{
	double l,r;
	const bool operator <(const nod &tmp)const{if(r!=tmp.r)return r<tmp.r;return l>tmp.l;}
}e[1000006];int m=0;

int main()
{
	cin>>n>>h;
	for(int i=1;i<=n;i++) cin>>x[i]>>y[i];
	init();
	for(int i=3;i<n;i++) if(i%2) e[++m]={l[i],r[i]};
	sort(e+1,e+1+m);
	
	double lst=-1e18;
	for(int i=1;i<=m;i++)
	{
		if(lst<e[i].l) anss++,lst=e[i].r;
	}
	
	cout<<anss<<'\n';
	return 0;
}