自动搬运

查看原文

来自洛谷，原作者为

	Liquefyx 哦

搬运于2025-08-24 22:29:15，当前版本为作者最后更新于2023-04-23 16:43:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

2023-04-23：先吐槽一两句，洛谷这道题的题面是有问题的，原英文题面是要求为恰好第一次恢复原样，但翻译的题面没有体现出第一次这一限制条件 QAQ。

2024.1.11 update: 忽然发现题面改了，记录一下，留恋qwq，还补了个可能不是很详细的构造证明嘿嘿 (º﹃º )。

简化题意

已知有如图所示 $n$ 行 $m$ 列的图：

操作 $1$ 能选择一个以位置 $x,y\ (1\leq x \leq n-1,\ 1\leq y \leq m-1)$ 为左下角的相邻点组成的平行四边形，然后将这四个点顺时针旋转；

操作 $2$ 能选择一个以位置 $x,y\ (1\leq x \leq n-1,\ 1\leq y \leq m-1)$ 为左下角的相邻点组成的等边三角形，然后将这三个点顺时针旋转；

请构造一组操作次数小于等于 $5\times 10^5$ 的操作序列，使得执行 $k$ 次操作序列后，图恰好第一次恢复原样，没有满足要求的序列则输出 $-1$。

题目分析

如果我们将每一次执行操作序列后的位置与原位置连边，那么这个变换就能以总点数为 $n\times m$ 的一些环表示出来，既然是“恰好第一次恢复原样”，说明所有环的长度的最小公倍数就恰好为 $k$。

考虑到总点数和操作序列的次数的限制，我们应该使得总环长尽可能的小，那么我们就可以对 $k$ 分解质因数，表示为 $\prod^{o}_{i=1} p_i^{c_i}$，然后构造 $o$ 个环长分别为 $p_i^{c_i}$ 的环即可（剩下的点看作自环不管就行），可以证明如此构造的环的总环长（不算自环，下面的证明同样不考虑自环）最小：（感觉不如感性理解）

有一个显然的结论，一个序列 $\{a_n\}$ 的最小公倍数相当于把序列中的每个数 $a_k$ 质因数分解后，将每一个质数求最大的出现次数的幂乘起来，形式化地，若序列每个数 $a_k$ 可分解为 $\prod_{i=1}^m p_i^{c_{i,k}}$，设 $mx_i=\max_{k=1}^n c_{i,k}$，则 $lcm=\prod_{i=1}^m p_i^{mx_i}$，所以，在我们分解题目中的 $k$ 后（$k=\prod^{o}_{i=1} p_i^{c_i}$），对于每个 $p_i$，一定能在环长序列中找到一个数使得其能被 $p_i^{c_i}$ 整除，既然要总和最小，序列中有多个数能被 $p_i$ 整除的情况一定是不优的，不能整除 $k$ 的质数也肯定不能整除序列中的任何数，于是分析存在多个质数能整除同一个数的情况，若一个环长 $a$ 能被两个不同的质数 $p_i$、$p_j$ 整除（设 $a=p_i^{c_i}\times p_j^{c_j},p_i<p_j$），因为此时最小的情况为 $6=2\times 3$，会发现刚好 $6>2+3$，并且当 $c_j$ 不变时如果 $c_i+=1$，那么 $a$ 的增长量为 $a\times (p_i-1)$，$p_i^{c_i}+p_j^{c_j}$ 的增长量为 $p_i^{c_i}\times (p_i-1)$，显然 $a$ 的增长量更多（$p_i-1 \ge 1,p_j^{c_j} \ge 3$ 嘛），由于 $p_i<p_j$，则 $c_i$ 不变 $c_j+=1$ 的情况也一样，所以把 $a$ 拆成两个数 $p_i^{c_i}$ 和 $p_j^{c_j}$ 一定更优，$a$ 能被多个质数整除的情况同样可以分析得到拆 $a$ 更优的结论（其实光看 $c_i=1$ 的情况即可，因为若 $c_i$ 增长，$a$ 的增长量一定更多，而 $j$ 个质数的情况能看作是 $j-1$ 个质数的情况添上了一个质数 $p$，那么最后分析下来依旧是 $a$ 的增长量更多，所以可得该结论阿巴阿巴），综上，最优情况肯定是构造的 $o$ 个环长分别为 $p_i^{c_i}$ 的环。

接下来我们要考虑如何去一个一个把环给构造出来。

通过瞎搞模拟我们能够发现，进行 $1$ 次操作 $1$ 后再进行 $2$ 次操作 $2$，我们能够把一个以位置 $x,y\ (1\leq x \leq n-1,\ 1\leq y \leq m-1)$ 为左下角的相邻点组成的平行四边形内的 $x+1,y$ 和 $x+1, y+1$ 两个点交换，如下图，可以理解为先将绿色点移到红色点位置，然后因为蓝色、粉色点在等边三角形内相对位置依旧不变，能直接利用操作 $2$ 将蓝色、粉色点复原，而红色点顺便也就到达了绿色点原来的位置，这组操作十分特殊，我们可以称之为一次单位操作。

我们若是想交换 $x,y$、$x+1,y$ 我们可以先进行一次操作 $1$，然后再进行一次单位操作，最后再进行 $3$ 次操作 $1$ 将其余的点转回去，其他相邻位置都可以像这样进行交换。

于是我们可以总结一下：对于任意相邻位置，我们可以将其放在一个满足操作 $1$ 的平行四边形内，先进行操作 $1$ 将这对相邻点放在单位操作能够进行交换的位置（即这个平行四边形的上边），然后进行单位操作，最后再把其他点用操作 $1$ 复原。

既然有了交换任意两个相邻点的方案，这题便迎刃而解惹，我们直接在一条相邻点连成的、能覆盖整张图的链上（比如蛇形填数、$S$ 路线遍历都可以，如下图）通过交换操作构造变换——那 $o$ 个环长分别为 $p_i^{c_i}$ 的环即可（从环的起始位置到终止位置，每两个点交换一次），至于为什么选择这种链，是因为遍历方便，而且这样做不会有多余的交换操作、交换次数最少，而操作序列的长度最多为 $n\times m\times 7$，能够满足条件。

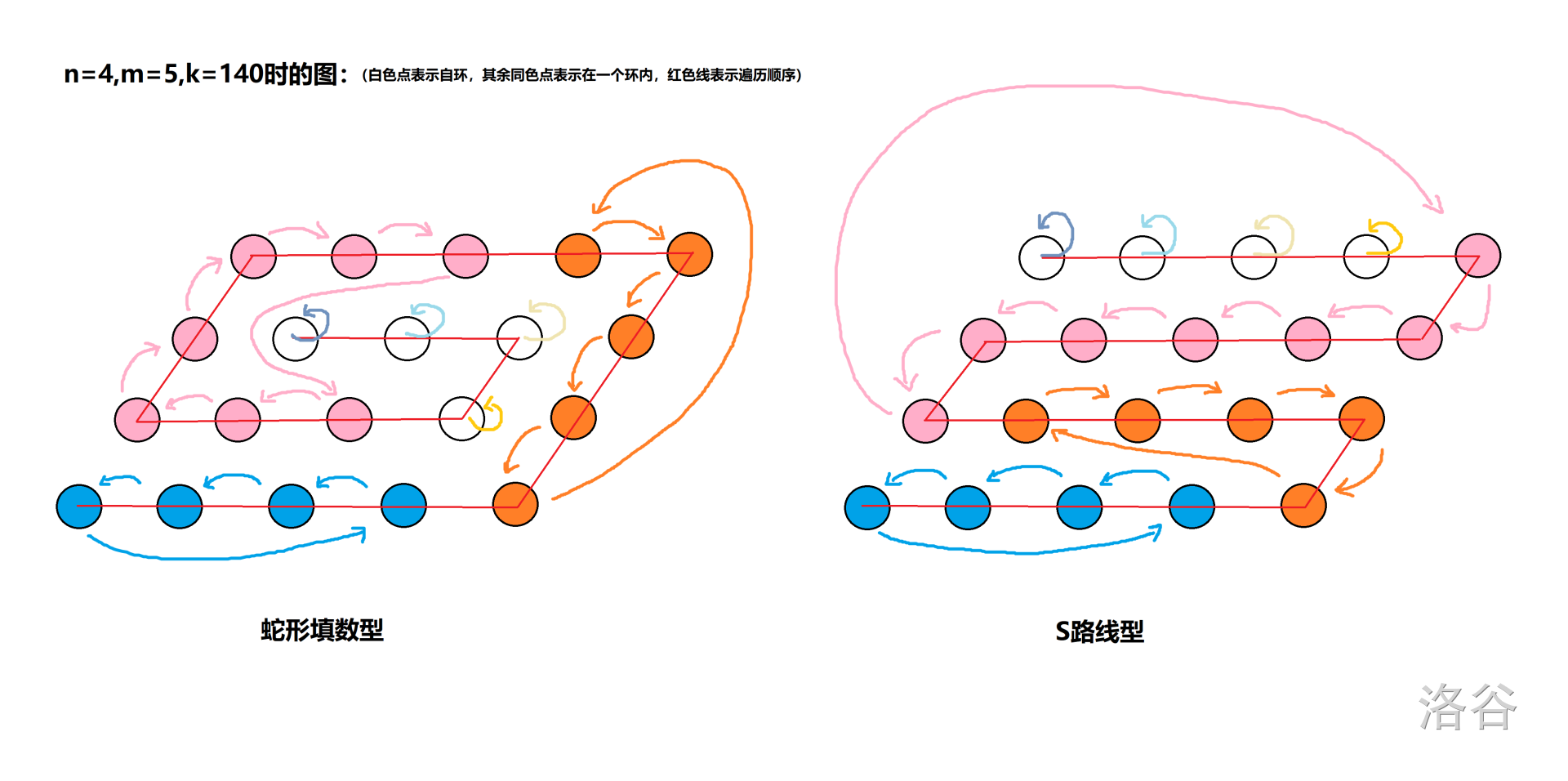
具体细节详见代码：

#include <bits/stdc++.h>
#define inLL long long
using namespace std;
int n, m, x, y, az, tot;
inLL k;
struct out {
	char a;
	int x, y;
}ans[500005];

template <typename T> void read(T& x) {
	x = 0; int f = 0; char c = getchar();
	while(c < '0' || c > '9') f |= (c == '-'), c=getchar();
	while(c >= '0' && c <= '9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
	x=(f ? -x : x);
}
int lne; char put[105];
template <typename T> void write(T x, char ch) {
	lne = 0; if(x < 0) putchar('-'), x=-x;
	do { put[++lne]=x%10, x/=10; } while(x);
	while(lne) putchar(put[lne--]^48);
	putchar(ch);
}
void one(int xx, int yy) {//一次单位操作 
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'T', xx, yy};
	ans[++tot]=out{'T', xx, yy};
}
void up(int xx, int yy) {//交换平行四边形的上边两点 
	one(xx, yy);
}
void down(int xx, int yy) {//交换平行四边形的底边两点 
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'R', xx, yy};
	one(xx, yy);
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'R', xx, yy};
}
void left(int xx, int yy) {//交换平行四边形的左边的两点 
	ans[++tot]=out{'R', xx, yy};
	one(xx, yy);
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'R', xx, yy};
}
void right(int xx, int yy) {//交换平行四边形的右边的两点
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'R', xx, yy};
	ans[++tot]=out{'R', xx, yy};
	one(xx, yy);
	ans[++tot]=out{'R', xx, yy};
}
void nxt() {
	(x&1 ? ((y^m) ? ++y : ++x) : ((y^1) ? --y : ++x));
	//s型路线遍历嘻嘻,用了位运算和三目运算符优化:
	//x为奇数时,若y等于m则x+1,否则y+1;
	//x为偶数时,若y等于1则x+1,否则y-1;
}
void solve(inLL k/*当前需要构造的环长*/) {
	if(k > az) {//剩余点数不够了,一定无解,输出-1
		puts("-1");
		exit(0);
	}
	az-=k;//计算剩余点数 
	for(int o = 1; o <= k-1; ++o)
		(x&1 ? ((y^m) ?  ((x^1) ? up(x-1, y) : down(x, y)): right(x, y-1)) :
		((y^1) ? up(x-1, y-1) : left(x, y))), nxt()/*交换下一处*/;
	//进行交换操作,此处依旧用了位运算和三目运算符优化:
	//x为奇数时,若y等于m则取右下角为(x-1,y)的平行四边形交换右边两点,否则判断x是否等于1,
	//等于1则取右下角为(x,y)的平行四边形交换下边两点,不等于1就取右下角为(x-1,y)的平行四边形交换上边两点;
	
	//x为偶数时,若y等于1则取右下角为(x,y)的平行四边形交换左边两点,否则直接取右下角为(x-1,y-1)的平行四边形交换上边两点
	
	nxt();//这个环构造玩了,走到下个环的起始位置 
}

signed main() {
	read(n), read(m), read(k);
	x=y=1, az=n*m;
	for(inLL i = 2; i*i <= k; ++i) {
		if(k%i) continue;
		inLL pp = 1;
		while(!(k%i))
			pp*=i, k/=i;//分解k 
		solve(pp);//构造环 
	}
	if(k^1)
		solve(k);
	write(tot, '\n');//输出,详见题目"输出格式"部分 
	for(int i = 1; i <= tot; ++i)
		putchar(ans[i].a), putchar(' '), write(ans[i].x, ' '), write(ans[i].y, '\n');
	return 0;
}

芜湖，完结撒花 ヾ(◍°∇°◍)ﾉﾞ。