自动搬运

查看原文

来自洛谷，原作者为

	zesqwq 达标啦！耶 ⊙ω⊙

搬运于2025-08-24 22:29:00，当前版本为作者最后更新于2023-05-11 20:08:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这个题空间 $O(\dfrac {n^2} w)$ 的做法即使你分批做也会被卡常。

考虑先用 $\texttt{bitset}$ 做传递闭包，具体就是每 $w$ 个分为一块，表示在一个 ull 里面，然后每次使用拓扑序来计算可达性，空间复杂度 $O(n)$，时间复杂度 $O(\dfrac {n^2} w)$，然后就可以获得一个矩阵，然后原问题就变为了二维数点，做法如下：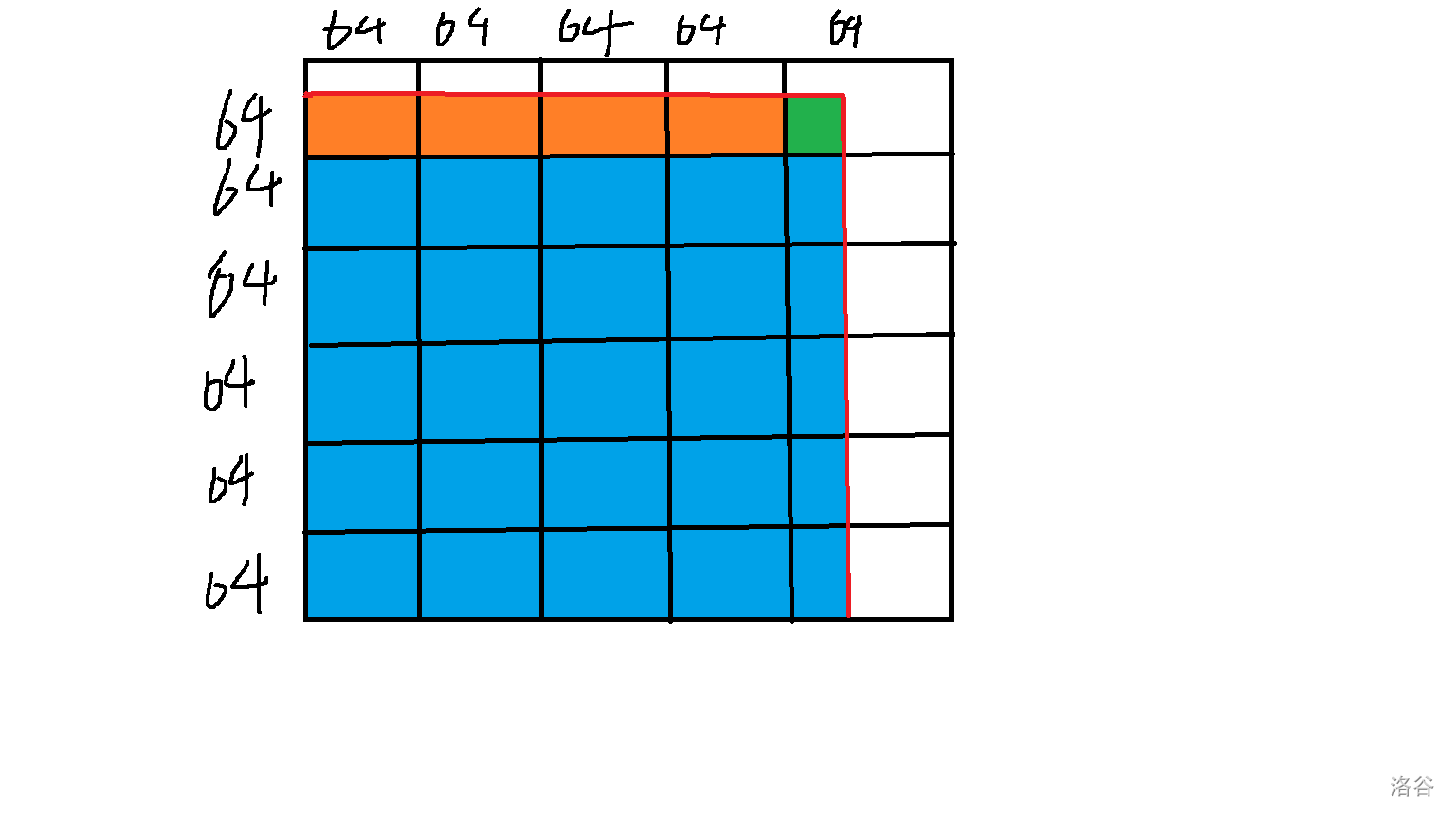

对于蓝色的部分，我们考虑计算 $\dfrac n w$ 轮，每一轮计算对于每一个点是否能被当前的 $w$ 个点到达，我们发现我们一次可以求出如下部分的值（红色代表我们 ull 存储的东西）。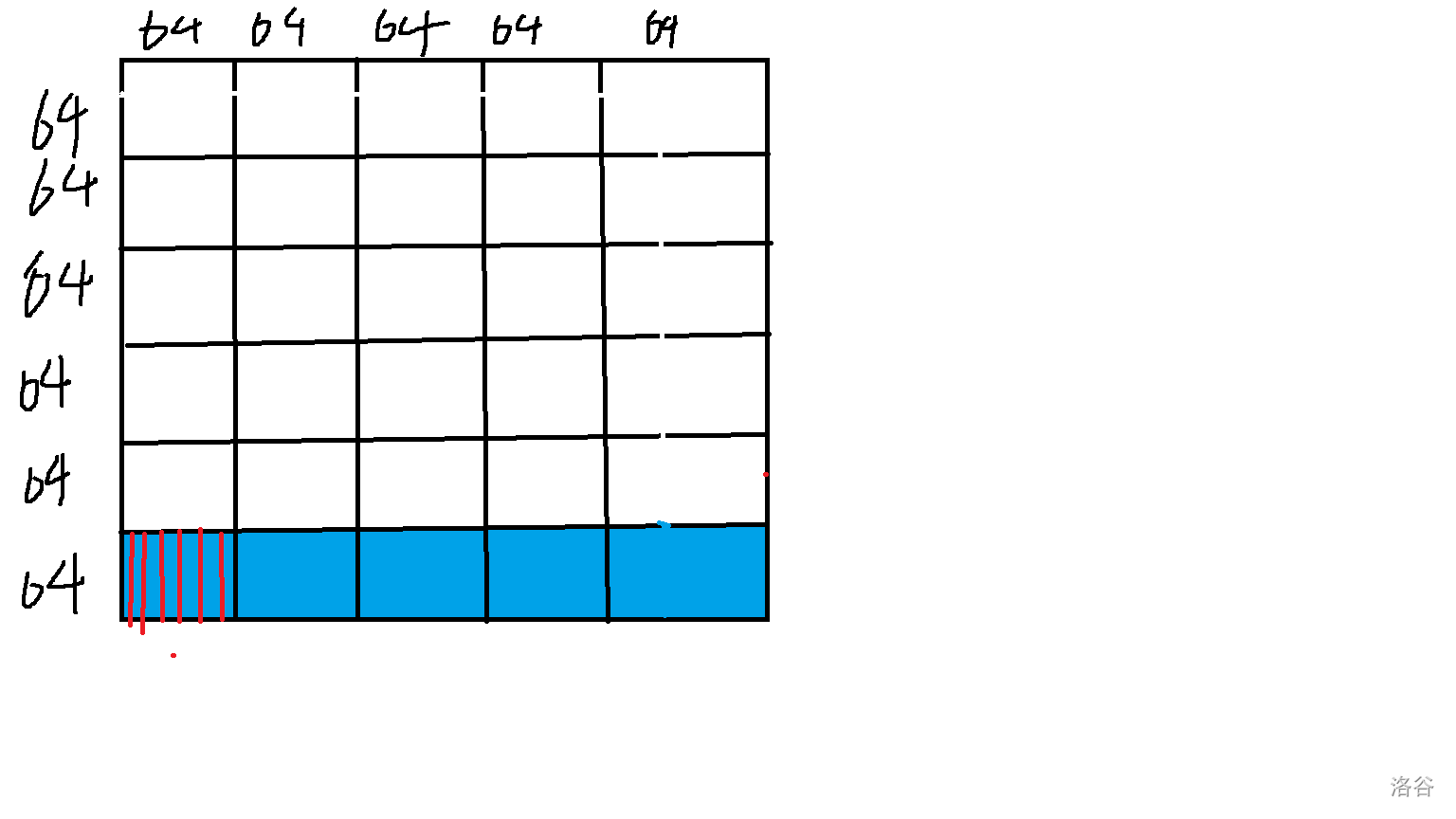

知道这个我们就可以解决蓝色部分的问题，然后就可以从下往上扫描线，每一次就是形如加一行，求二维前缀和，因为我们只关心新增的一行的前缀和，所以可以做到单轮空间复杂度和时间复杂度 $O(n)$。

总的时间复杂度 $O(\dfrac {n^2} w + q)$，空间线性。

对于橙色部分，我们解决它的方法本质就是蓝色转了 $90$°，本质相同。

对于绿色部分，我们发现它只是一个 $O(w^2)$ 的矩阵，然后有因为我们已知的信息是一个横着或者竖着的 ull，刚好 and 一下我们要求的范围再 popcount 一下即可，注意到 1ull << 64 是 $\text{UB}$，时间复杂度 $O(\dfrac {n^2} w + qw)$。

综上，我们已经在 $O(\dfrac{n^2} w + qw)$ 的时间复杂度内解决了该问题，因为要离线所以空间 $O(n+q)$，精细实现可以通过。

#pragma GCC target("popcnt")
template <typename X, typename Y>
inline void readp(pair<X, Y> &p) {
    read(p.first), read(p.second);
}
template <typename T>
inline void clear(T &x) {
    T y;
    swap(x, y);
}
const int N = 1e5 + 1000, Q = 1e6 + 10;
vector<int> vec[N];
ull f[N], f2[N];
int du[N], n, m, cur, fa[N], T, L, R, q[N], l, r, id[N], tcnt, bfncnt;
ll ans[Q];
vector<pair<int, int> > q1[N], q2[N];
vector<tuple<int, int, int> > q3[N];
inline void ptopo() {
    l = 1, bfncnt = r = 0;
    for (int i = 0; i < n; i++)
        if (!du[i]) q[++r] = i;
    int u;
    while (l <= r) {
        id[++bfncnt] = u = q[l++];
        for (int v : vec[u]) {
            f2[v] |= f2[u];
            if (!--du[v]) q[++r] = v;
        }
    }
}
inline void topo() {
    memset(f, 0, sizeof(f)), memset(f2, 0, sizeof(f2));
    for (int i = L; i <= R; i++) f[i] |= 1ull << i - L, f2[i] |= 1ull << i - L;
    for (int i = n; i; i--)
        for (int v : vec[id[i]]) f[id[i]] |= f[v];
    for (int i = 1; i <= n; i++)
        for (int v : vec[id[i]]) f2[v] |= f2[id[i]];
}
ll p[N], p2[N], val[N], nval[N];
inline void solve() {
    topo();
    for (int i = 0; i < n; i++)
        val[i] = __builtin_popcountll(f[i]),
        nval[i] = __builtin_popcountll(f2[i]);
    for (int i = 1; i < n; i++) {
        if ((i >> 6) == (i - 1 >> 6)) nval[i] += nval[i - 1];
        val[i] += val[i - 1];
    }
    for (int i = 0; i < n; i++) p[i] += val[i], p2[i] += nval[i];
    for (auto [x, id] : q1[cur])
        if (id >= 1)
            ans[id] += p[x];
        else
            ans[-id] -= p[x];
    for (auto [x, id] : q2[cur])
        if (id >= 1)
            ans[id] += p2[x];
        else
            ans[-id] -= p2[x];
    for (auto [x, y, id] : q3[cur]) {
        ull pre = ((1ull << y) - 1ull);
        for (int i = (x >> 6) << 6; i <= x; i++) {
            if (y == 64) {
                if (id >= 1)
                    ans[id] += __builtin_popcountll(f[i]);
                else
                    ans[-id] -= __builtin_popcountll(f[i]);
            } else {
                if (id >= 1)
                    ans[id] += __builtin_popcountll(pre & f[i]);
                else
                    ans[-id] -= __builtin_popcountll(pre & f[i]);
            }
        }
    }
}
inline void solve(int r, int h, int id, int f) {
    if (r >= 64) q1[(r >> 6) - 1].push_back({h, id * f});
    if (h >= 64) q2[(h >> 6) - 1].push_back({r, id * f});
    q3[r >> 6].push_back({h, r - ((r >> 6) << 6) + 1, id * f});
}
int main() {
    read(n), read(m);
    int u, v;
    for (v = 1; v < n; v++) read(u), --u, vec[u].push_back(v), ++du[v];
    for (int i = 1; i <= m; i++)
        read(u), read(v), --u, --v, vec[u].push_back(v), ++du[v];
    ptopo(), read(T);
    for (int i = 1; i <= T; i++) {
        read(u), read(v), --u, --v;
        solve(v, v, i, 1);
        if (u)
            solve(u - 1, u - 1, i, 1), solve(u - 1, v, i, -1),
                solve(v, u - 1, i, -1);
    }
    for (int i = 0; i <= (n >> 6); i++) L = (cur = i) << 6, R = L + 63, solve();
    for (int i = 1; i <= T; i++) write(ans[i]), putc('\n');
    do_flush();
    return 0;
}