自动搬运

查看原文

来自洛谷，原作者为

	wsyhb **

搬运于2025-08-24 22:28:26，当前版本为作者最后更新于2021-01-23 23:20:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意简述

给定一棵 $n$ 个节点的树，第 $u$ 个点的权值为 $a_u$。有 $q$ 次查询，每次询问给出一个编号 $id$，表示询问“删除第 $id$ 条边和其余某条边后 $3$ 个连通块点权和的乘积”的所有情况之和。

数据范围：$n,q \le 10^6$

分析 + 题解

由于询问数量 $q$ 与 $n$ 同阶，该问题需要对任意一个连通块求点权和以及删除其中某条边后的 $2$ 个连通块点权和乘积的所有情况之和，前一个问题很好处理，后一个问题不难想到换根（严格来说不算 DP）。

此处以对以 $x$ 为根的子树求解上述问题为例进行讲解。

设 $x$ 子树的点权和为 $sum_x$，对 $x$ 子树求解上述问题所得结果为 $ans_x$，则有：

$$ans_x=\sum_{y \in subtree_x}sum_y(sum_x-sum_y)=sum_x \cdot (\sum_{y \in subtree_x} sum_y)-(\sum_{y \in subtree \;x} sum^2_y) $$

其中 $subtree_x$ 表示 $x$ 子树中包括 $x$ 的点组成的集合。

设 $dp_x=\sum_{y \in subtree_x} sum_y$，$dp2_x=\sum_{y \in subtree_x} sum^2_y$，则上式化简为：

$$ans_x=sum_x \cdot dp_x - dp2_x$$

而 $dp_x$ 和 $dp2_x$ 都很好求：

$$dp_x=sum_x+\sum_{y \in son_x}dp_y ,dp2_x=sum^2_x+\sum_{y \in son_x}dp2_y $$

再加上这是一个求和式，无需采用“前缀+后缀”的换根形式，只需使用简单的换根即可，具体实现见代码。

代码

#include<bits/stdc++.h>
using namespace std;
const int P=99991;//注意模数 
inline void add(int &a,int b)
{
	a=a+b-(a+b>=P?P:0);
}
inline void sub(int &a,int b)
{
	a=a-b+(a-b<0?P:0);
}
inline int get_sum(int a,int b)
{
	return a+b-(a+b>=P?P:0);
}
inline int get_dif(int a,int b)
{
	return a-b+(a-b<0?P:0);
}
inline int get_pro(int a,int b)
{
	return 1ll*a*b%P;
}
inline int get_square(int x)
{
	return 1ll*x*x%P;
}
//以上是模意义运算 
const int max_n=1e6+5;
int End[max_n<<1],Last[max_n],Next[max_n<<1],e;
inline void add_edge(int x,int y)
{
	End[++e]=y;
	Next[e]=Last[x];
	Last[x]=e;
	End[++e]=x;
	Next[e]=Last[y];
	Last[y]=e;
}
int a[max_n],fath[max_n],sum_in[max_n],dp_in[max_n],dp2_in[max_n];//in 表示子树内 
void dfs1(int x,int fa)
{
	fath[x]=fa;
	sum_in[x]=a[x];
	for(int i=Last[x];i;i=Next[i])
	{
		int y=End[i];
		if(y!=fa)
		{
			dfs1(y,x);
			add(sum_in[x],sum_in[y]);
			add(dp_in[x],dp_in[y]);
			add(dp2_in[x],dp2_in[y]);
		}
	}
	add(dp_in[x],sum_in[x]);
	add(dp2_in[x],get_square(sum_in[x]));
}
int sum_out[max_n],dp_out[max_n],dp2_out[max_n],sum_all;//out 表示子树外 
void dfs2(int x,int fa)
{
	if(fa!=0)
	{
		dp_out[x]=get_sum(dp_out[fa],sum_out[x]);//这两项分别对应下图的红色和黄色部分 
		add(dp_out[x],dp_in[fa]);
		sub(dp_out[x],get_sum(sum_in[fa],dp_in[x]));//这两行对应下图中的蓝色部分 
		dp2_out[x]=get_sum(dp2_out[fa],get_square(sum_out[x]));
		add(dp2_out[x],dp2_in[fa]);
		sub(dp2_out[x],get_sum(get_square(sum_in[fa]),dp2_in[x]));
	}
	for(int i=Last[x];i;i=Next[i])
	{
		int y=End[i];
		if(y!=fa)
			dfs2(y,x);
	}
}
int ans_in[max_n],ans_out[max_n];//ans 与上文所述含义相同 
bool vis_in[max_n],vis_out[max_n];
inline int work_in(int x)//记忆化求解 
{
	if(vis_in[x])
		return ans_in[x];
	vis_in[x]=true;
	ans_in[x]=get_dif(get_pro(dp_in[x],sum_in[x]),dp2_in[x]);
	return ans_in[x];
}
inline int work_out(int x)
{
	if(vis_out[x])
		return ans_out[x];
	vis_out[x]=true;
	ans_out[x]=get_dif(get_pro(dp_out[x],sum_out[x]),dp2_out[x]);
	return ans_out[x];
}
int u[max_n],v[max_n];//存储边的端点 
int main()
{
	int n,q;
	scanf("%d%d",&n,&q); 
	for(int i=1;i<=n;++i)
	{
		scanf("%d",a+i);
		a[i]%=P;//记得读入时模一次 
		add(sum_all,a[i]);//sum_all 记录 n 个点的点权和 
	}
	for(int i=1;i<=n-1;++i)
	{
		scanf("%d%d",u+i,v+i);
		add_edge(u[i],v[i]);
	}
	dfs1(1,0);
	for(int i=1;i<=n-1;++i)
	{
		if(fath[v[i]]==u[i])
			swap(u[i],v[i]);//使 u[i] 是 v[i] 的儿子 
	}
	for(int i=1;i<=n;++i)
		sum_out[i]=get_dif(sum_all,sum_in[i]);
	dfs2(1,0);
	long long ans1=0;//开 long long 
	int ans2=0;
	while(q--)
	{
		int id;
		scanf("%d",&id);
		int x=u[id];
		int ans=get_pro(work_in(x),sum_out[x]);//讨论删除 x 子树内边的情况 
		add(ans,get_pro(sum_in[x],work_out(x)));//讨论删除 x 子树外边的情况
		ans1+=ans,ans2^=ans;
	}
	printf("%lld\n%d\n",ans1,ans2);
	return 0;
}

代码中提到的图片如下：

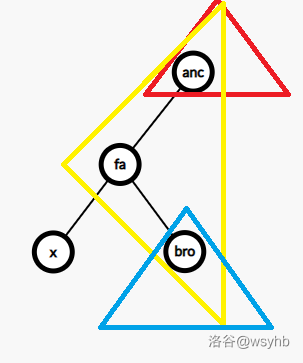
可结合图片理解换根部分的代码。