自动搬运

查看原文

来自洛谷，原作者为

	Mivik AFO

搬运于2025-08-24 22:28:13，当前版本为作者最后更新于2021-01-02 21:39:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

欢迎到我的博客查看

满分做法

我们还是把括号序列转换成那个经典的“走右上右下”的形式，即从 $(0,0)$ 开始行走，左括号是向右上走，右括号是向右下走，那么一个括号序列合法等价与行走轨迹不越过 X 轴。比如下图是 ()(()) 对应的行走轨迹：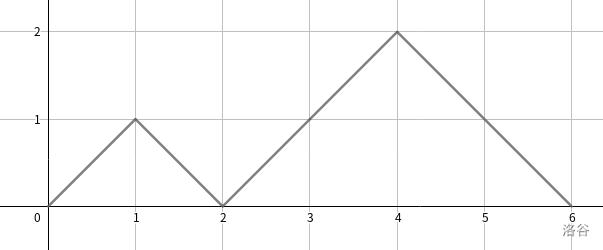

我们发现，算法最开始随机 random_shuffle 出来的括号序列，对应着一个可能越过了 X 轴，但最终走到了 $(2n,0)$ 的行走轨迹（因为左括号右括号数目相等）。然后仔细观察我们的算法，实际上就是找到第一个低于 X 轴的位置和在这个位置后第一次走回 X 轴的位置，并把中间的一段翻到 X 轴上去了。这样必定能形成最终的合法括号序列。

于是答案就显而易见了。由于在翻转过程中我们的行走轨迹中与 X 轴相交的那些点是不变的，所以如果一个合法的括号序列对应的行走轨迹有 $m$ 个点与 X 轴相交，它就可能由 $2^{m-1}$ 次方种括号序列得到（每一个部分在 X 轴上方或者下方），所以答案就是 $\frac{2^{m-1}}{\binom{2n}n}$。

mivik.h

代码