自动搬运

查看原文

来自洛谷，原作者为

	XUAN— 扶摇直上九万里

搬运于2025-08-24 22:27:49，当前版本为作者最后更新于2021-10-01 00:56:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

蔬菜庆典

题目

打个广告 XUAN

据说数据很水，所以蒟蒻也不知道自己写对没，欢迎指正（小声）

题目大意 ： 给定一棵带点权的树，可修改 节点 $w_x=w_1+w_2-w_x$ ($w_1$ 为 $x$ 父节点的值，$w_2$ 为$x$任意子节点的值 )——修改操作可任意进行，问最终最大点权和（可为正无穷）

分类思考：

+inf

到底什么情况下才是正无穷呢？根据样例不难发现，如果一个可操作节点拥有两个值不相同的儿子，那么反复操作，答案就会不断累加，可以达到正无穷。显然地，一条链是无法变成+inf的，尝试手动模拟一下就会发现，点权值只能随修改反复横跳。

那么，儿子的值都相同就一定不是正无穷了嘛？显然不是的，因为，若其中一个儿子的可以被改变(即$2 * w_x！=w_1+w_2$ )那么就等同有两个不同的儿子，这也是成立的。

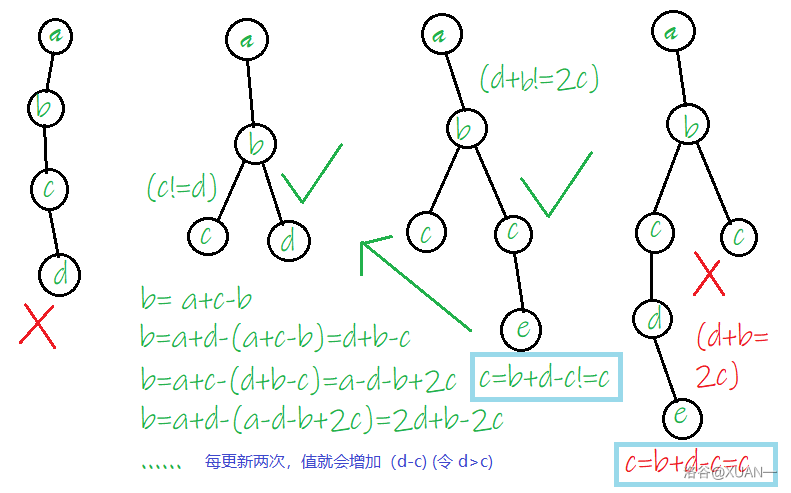
求最大值

接下来就是求最大值，显然，我们只需要考虑链的情况，因为对于有分叉的情况，既然它无法构成 +inf 的情况，一定是所有儿子值相同且不能改变，（不算根节点处的分叉） 那么直接统计其初值就好了（我维护了子树和）

现在来思考一下链的情况，按正常人的思路——可以贪心吗？ 怎么贪心？——让我们来把规律进行一个找

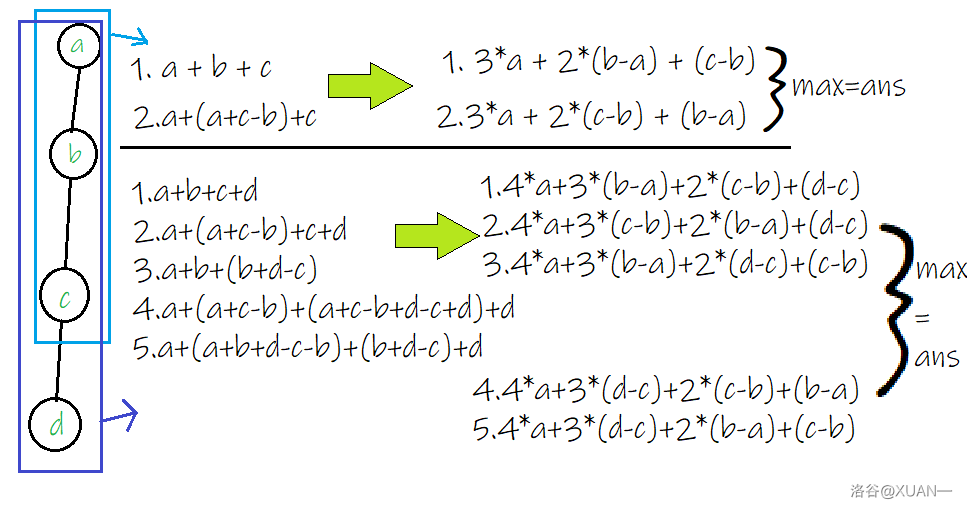
好吧，虽然有点奇妙 （确实不是人能想出来的） ，但显然，最终答案是一个固定的序列——以儿子减父亲的值作为一项，各项系数分别为 $1$ 至 $n$ ,贪心地把较大项的系数给到更大即可。（显然和大佬们的差分是等价der）

最后给到代码，感谢同机房的巨们帮忙改了一下，虽然很丑，但至少还是能看懂（前方大佬给的码太时尚了，我痛苦了好久）

Code

#define M 200005//author : XUAN
#define LL long long
#define inf 0x3f3f3f
using namespace std;
int h[M],to[M],pre[M],d,son[M],n,fa[M],Root;
LL w[M],sum[M],ans;
void add(int a,int b)
{d++;pre[d]=h[a];h[a]=d;to[d]=b;}
bool flag1,flag4,flag2,flag3,Flag;
LL yezi;
void dfs(int x)
{ 
     if(flag1||(flag2&&flag3))return;
     sum[x]+=w[x];
     LL Pre=inf; // 前个儿子的值 
    if(son[x]==0){yezi+=w[x]; return ;} //叶子 
    if(fa[x]!=Root && son[x]!=0 && son[fa[x]]>1) flag3=1; // 前分叉  
    if(son[x]>1) flag4=1;// 分叉  
    for(int i=h[x];i;i=pre[i])
    {
        if(w[fa[x]]+w[to[i]]!=2*w[x]) flag2=1; // x 点值可改 
        if(Pre!=inf && w[to[i]]!=Pre) flag1=1; //两个不一样的儿子 
        Pre=w[to[i]];
        dfs(to[i]);
        sum[x]+=sum[to[i]]; //子树和 
    }  
    return ;
}
LL cf[M],top; //答案数组 
bool cmp(int x,int y)
{return x>y;}
LL find(int x)
{ 
    flag1=flag4=flag2=flag3=0;yezi=0;
    dfs(x);
    if(flag1||(flag2&&flag3))return 0; // x 有两个不一样的儿子 || fa[x] 有两个不一样的儿子（x可以变） 
    if(flag4&&flag3)return sum[x]; // 分叉点 （直接统计答案) 
    top=0;//留下的就是链了 
    for(int i=x;;i=to[h[i]])
    {
        cf[++top]=w[i]-w[fa[i]];
        if(h[i]==0)break; // 链尾 
    }
    sort(cf+1,cf+top+1,cmp);
    LL now=w[Root];
    LL sum=0;
    for(int i=1;i<top;i++)  //注意尾巴（叶子）不要重复加
    {
        now+=cf[i];
        sum+=now;
    }
    return sum+yezi;
}
void cl()
{	
	d=0;ans=0;Flag=0;yezi=0;
	memset(h,0,sizeof(h));
	memset(son,0,sizeof(son));
	memset(sum,0,sizeof(sum));
}
int main()
{
    while(1)
    {
    	cl();
		scanf("%lld",&n); 
        if(n==0)break;
        for(int i=1;i<=n;i++)
        {
            scanf("%d%lld",&fa[i],&w[i]);
            if(fa[i]!=-1) add(fa[i],i),son[fa[i]]++;
            else Root=i;
        }
        for(int i=h[Root];i;i=pre[i])
        {
            LL temp=find(to[i]);//遍历所有根节点的儿子
            if(flag1||(flag2&&flag3)){Flag=1;break;} 
            ans+=temp;
        }
        if(Flag)printf("+inf\n");
        else printf("%lld\n",ans+w[Root]);    
    }
    return 0;
}