自动搬运

查看原文

来自洛谷，原作者为

	guoziyu_2023CSP 最后在线时间：2025年8月24日9时37分 || 2023CSP-J/S RP++ || 一个编程小白, 私信互关!(已作废) || 不CSP-J一等不改 个性签名！ 已经两次了: ）

搬运于2025-08-24 22:27:41，当前版本为作者最后更新于2025-07-24 15:56:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

由题可知：

1. 一个连通块可能为一个动物踩出。

2. 每个地方的脚印都为最新的，故包含起点与终点的连通块为最后一直动物。

3. 覆盖过的脚印可能为任意一只动物，求动物最少数量时应将覆盖过的脚印当做此动物的。即加入此动物脚印所在连通块。（如下图，红色为最后一只，红线为其轨迹，则绿色可能经过所有红点）

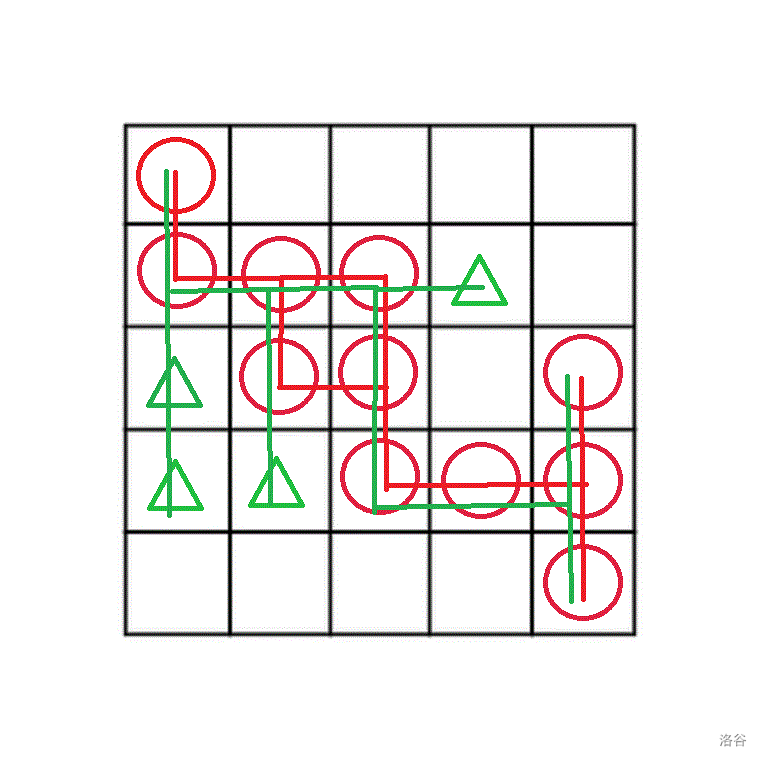
话不多说，上代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
const int dx[4] = {0,0,1,-1};
const int dy[4] = {1,-1,0,0};
int n,m,mp[N][N],cnt;
bool flag[N][N]; string s;
queue<int> qx,qy,nxtx,nxty;
void BFS(){
	qx.push(1); qy.push(1);
	while(!qx.empty()){
		int nx = qx.front();//现在的x
		int ny = qy.front();//现在的y
		qx.pop(); qy.pop();
		if(flag[nx][ny]){
			continue;
		} flag[nx][ny] = 1;
		for(int i = 0;i < 4;i++){
			int tx = nx + dx[i];//要去的x
			int ty = ny + dy[i];//要去的y
			if(tx < 1 || tx > n || ty < 1 || ty > m
			|| flag[tx][ty]) continue;//越界或访问过 
			if(mp[tx][ty] == mp[nx][ny]){
				qx.push(tx); qy.push(ty);
			}else if(mp[tx][ty] == !mp[nx][ny]){//连通但不是一种脚印，存入当做下一只动物的 
				nxtx.push(tx); nxty.push(ty);
			}
		}
	} return ;
} main(){
	cin >> n >> m;
	for(int i = 1;i <= n;i++){
		cin >> s;
		for(int j = 1;j <= m;j++){
			if(s[j - 1] == '*'){
				mp[i][j] = 2;
			}else if(s[j - 1]=='T'){
				mp[i][j] = 0;
			}else mp[i][j] = 1;
		}
	} for(int i = 1;i <= n * m;i++){
		BFS();
		if(nxtx.empty()){//遍历完了 
			cout << i << "\n";
			return 0;
		} while(!nxtx.empty()){
			qx.push(nxtx.front());
			qy.push(nxty.front());
			nxtx.pop(); nxty.pop();
		}
	} return 0;
}//完结撒花，RP++ 

蒟蒻的第一篇题解，求过。（没有能写题解的水题）