自动搬运

查看原文

来自洛谷，原作者为

	Liynw https://liynw.top/ | AFOed(2021.1~2022.6).

搬运于2025-08-24 22:27:23，当前版本为作者最后更新于2021-09-13 23:06:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目链接

记忆化搜索，其实思路不太难吧，但是优化比较难想，建议评蓝。

---

题意简述：

有一个 $m\times n$ 的方格矩阵，把这个矩阵分为若干部分，且要求每一个矩阵都要与边界相邻。令 $k$ 为标准面积，不满意度为{所有矩阵面积减去 $k$ 的平方}之和。求最小的不满意度。

---

搜索

题库里有道题叫生日快乐（这道题是蓝的，但是难度严重虚高，个人觉得最多是绿），其实思路相仿，不过这题要难一些。

我们假设拿到了一个已知所有信息、且满足四周有边界的矩阵，我们要对它进行搜索。

首先我们要解决传参问题：什么算已知条件，而且如何判断这个矩阵是不是满足条件呢？

首先长和宽是有必要的。而且因为这道题要求每一个矩阵都要挨着边界，所以我们需要知道它四面挨着边界的情况。

dfs 函数中传 $6$ 个参数：

• int 类型：$x$ （矩阵的长），$y$ （矩阵的宽）。

• bool 类型：up （此矩阵上面那条边是否挨着边界），down （下面那条边是否挨着边界），left （左边那条边是否挨着边界），right （右边那条边是否挨着边界）。

---

解决完了 dfs 函数的传参问题，那怎么搜索呢？

我们先来分析出口。

由于题目要求，只要已知一个矩阵四面都没挨着边界，就直接返回一个极大值。

对于一个满足条件且已知的矩阵，有两种思路：

1. 直接把它作为一个最终划分的矩阵；

2. 把它继续分成更小的矩阵。

第一种思路很好解决，直接按照长、宽求就行了。

关键是第二种。

为了方便大家理解，我随便画了一个矩阵举例说明：

（Excel 真好用啊，蓝色为边界的外面那一圈）

对于这个矩阵，我们又有两种划分的方法：

1. 横着切；

（红色的地方就是能切的地方。）

2. 竖着切。

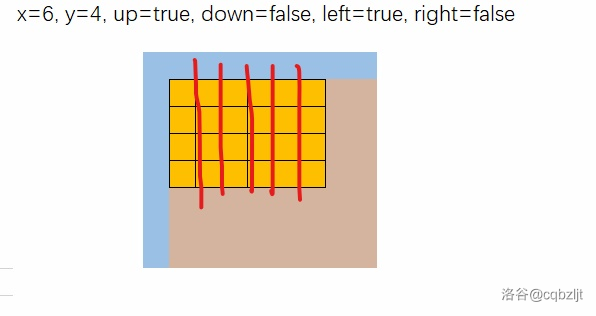
那我们只需要分两种情况，分别枚举切割的地方，寻找最小值就可以了。（比如说，枚举上面/左边那个矩阵的长/宽）

最后再看一下哪种情况会更好。

注意一个细节：横着切需满足 $x>1$，竖着切需满足 $y>1$。

核心代码大概长这样：

if(!(up||down||left||right)) return inf; //不沿海 
ll ans1=pow(x*y-k,2);
if(x==1&&y==1) return ans1;
ll ans2=inf;
bool u1,u2,d1,d2,l1,l2,r1,r2;
//横着分开
u1=up,u2=0,d1=0,d2=down,l1=l2=left,r1=r2=right;
if(x>1){
    for(int i=1;i<x;i++){
        int t=dfs(i,y,u1,d1,l1,r1)+dfs(x-i,y,u2,d2,l2,r2);
        ans2=min(ans2,t);
    }
}
//竖着分开 
u1=u2=up,d1=d2=down,l1=left,l2=0,r1=0,r2=right;
if(y>1){
    for(int i=1;i<y;i++){
   	int t=dfs(x,i,u1,d1,l1,r1)+dfs(x,y-i,u2,d2,l2,r2);
        ans2=min(ans2,t);
    }
}
return min(ans1,ans2);

---

记忆化

开一个六维的数组 $dp$，每一维都对应一个传的参数，把 dfs 的值存在里面即可。

这个时候有人就会说了：可是不一样的矩阵可能六个参数都一样，那这个如何判断？

答案是不需要判断。虽然的确这种情况是存在的，但是，如果六个参数都一样，算出来的结果肯定也一样，这不会影响结果，还会减小运行的时间。

---

剪枝

• 可行性剪枝

观察一下上面的图，不难发现，有一些情况是不能做横着或者竖着的分割的，比如说这种：

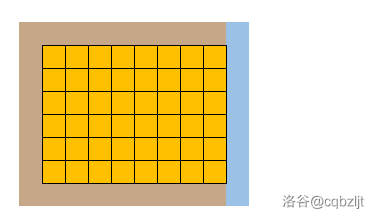
这个东西就不能竖着切，因为如果竖着切了，左边的那个矩阵就不挨着边界了。

那我们可以写出矩阵要横着切和竖着切的条件：

• 横着：up&&down||left||right

• 竖着：left&&right||up||down

为什么呢？以横着切举例：

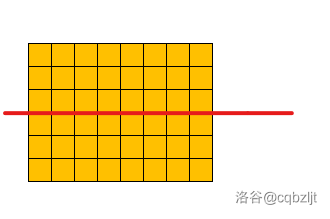
现在四面是否挨着边界不知道。

如果要求成功，就必须满足下列至少一个条件：

1. 上面和下面都挨着边界。

2. 左边挨着边界，或者右边挨着边界。

你们自己去想一想，竖着也类似。

• 最优性剪枝

很好想，要是一个矩阵的面积小于 $k$，就不继续切了，直接返回。

• 等价性剪枝

zszz 矩阵是可以转的对吧？

拿到一个矩阵之后，我们可以尝试把它转一下：可以向左旋转 $0^{\circ},90^{\circ},180^{\circ},270^{\circ}$，每一种旋转都可以查看是否已求出结果，如果有，直接返回。

代码比较简单，但是思考的过程比较绕：

if(dp[x][y][up][down][left][right]!=-1) return dp[x][y][up][down][left][right]; //正常 
if(dp[x][y][down][up][right][left]!=-1) return dp[x][y][down][up][right][left]; //倒立 
if(dp[y][x][left][right][down][up]!=-1) return dp[y][x][left][right][down][up]; //往左转 
if(dp[y][x][right][left][up][down]!=-1) return dp[y][x][right][left][up][down]; //往右转 

剪枝就这三个。虽然不多，但足以通过这道题。

最后再卡一下常。

---

Code

#include<cstdio>
#include<cmath>
#include<cstring>
#define min(a,b) (a)<(b)?(a):(b);
#define ll long long
const int maxn=305;
const ll inf=(ll)2e9;
int n,m,k;
ll dp[maxn][maxn][2][2][2][2];
ll dfs(int x,int y,bool up,bool down,bool left,bool right){ //bool 类型记录是否四个方向沿海 
	if(dp[x][y][up][down][left][right]!=-1) return dp[x][y][up][down][left][right]; //正常 
	if(dp[x][y][down][up][right][left]!=-1) return dp[x][y][down][up][right][left]; //倒立 
	if(dp[y][x][left][right][down][up]!=-1) return dp[y][x][left][right][down][up]; //往左转 
	if(dp[y][x][right][left][up][down]!=-1) return dp[y][x][right][left][up][down]; //往右转 
	if(!(up||down||left||right)) return inf; //不沿海 
	ll ans1=pow(x*y-k,2);
	if(x==1&&y==1||x*y<k) return dp[x][y][up][down][left][right]=ans1;
	ll ans2=inf;
	bool u1,u2,d1,d2,l1,l2,r1,r2;
	//横着分开 
	if(x>1&&(up&&down||left||right)){
		u1=up,u2=0,d1=0,d2=down,l1=l2=left,r1=r2=right;
		for(register int i=1;i<x;i++){
			int t=dfs(i,y,u1,d1,l1,r1)+dfs(x-i,y,u2,d2,l2,r2);
			ans2=min(ans2,t);
		}
	}
	//竖着分开 
	if(y>1&&(left&&right||up||down)){
		u1=u2=up,d1=d2=down,l1=left,l2=0,r1=0,r2=right;
		for(register int i=1;i<y;i++){
			int t=dfs(x,i,u1,d1,l1,r1)+dfs(x,y-i,u2,d2,l2,r2);
			ans2=min(ans2,t);
		}
	}
	return dp[x][y][up][down][left][right]=min(ans1,ans2);
}
int main(){
	memset(dp,-1,sizeof(dp));
	scanf("%d %d %d",&m,&n,&k);
	printf("%lld",dfs(m,n,1,1,1,1)); 
	return 0;
}