自动搬运

查看原文

来自洛谷，原作者为

	Z1qqurat 一条 2 米长的翻车鱼死在了我家后院

搬运于2025-08-24 22:27:16，当前版本为作者最后更新于2022-05-16 12:59:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

嗯，这道题虽然只是绿的，但个人认为其中有重要意义。由于这道题涉及到的算法和思路比较多，我会采用循序渐进的方式来写。

Part 1 基础做法

哈，先来理解一下题意吧。

个人是建议把题目里面滴图倒过来看看！

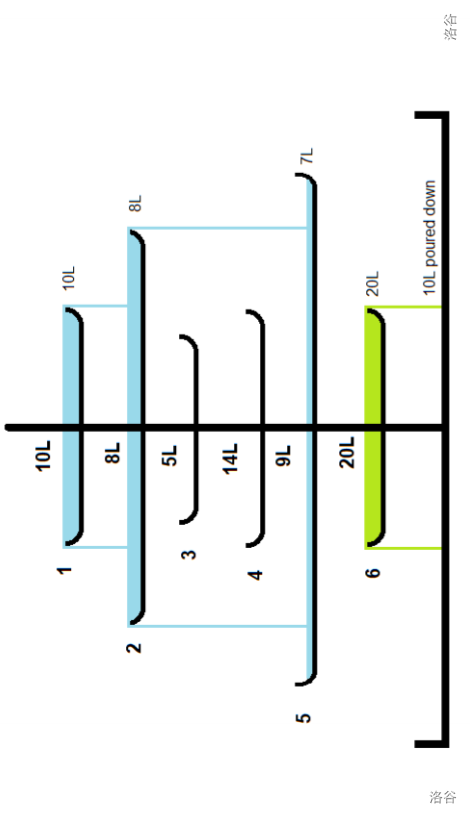
可以这么理解，如果水到了一个盘子里面，会溢出到往右第一个直径比所在盘子要大的盘子里面。

“后面第一个比自己大的元素”，这不就是单调栈的用法吗，所以我们可以自然地想到单调栈所有盘子的 $d_i$ （直径）。

于是可以写出下面代码咯：

void find_max(){
	for(ri i=1;i<=n;i++){
		while(stk.empty()==0&&d[i]>d[stk.top()]){
			b[stk.top()]=i;//记录每个盘子往右第一个直径比它大的盘子编号。
			stk.pop();
		}
		stk.push(i);
	}
	while(stk.empty()==0){
		b[stk.top()]=0;//0代表水池。
		stk.pop();
	}
}

那有了这个，我们再想想，接下来怎么做呢？就举一个浅显的例子，现在我们确定了一个盘子 $r$ （编号），里面装了 $v$ 的水，我们只需要不停地找它的下一个盘子，直到水不会再溢出就可以找到最后的盘子的编号了，这个过程可以用while循环实现：

for(ri i=1;i<=q;i++){
	scanf("%d%d",&r,&v);
	int tmp=r;
	while(tmp!=0){	
		v-=c[tmp];
		if(v<=0)break;
		tmp=b[tmp];
	}
	printf("%d\n",tmp);
}

那我们这么做，可以拿到30分（TLE），而这题在普及组中也大概有个3~4题的难度，大概会有个50分左右，也是不错的分了！

Part2 升级版正解

单调栈的部分肯定没得改滴了，现在我们就来想想如何优化。

有单调性，可以二分？但是考虑到如果要二分，就需要任意一段距离可以承受的水量，这个也不好算，和区间内每一个盘子的直径容积都有关系，直接放弃。

既然想到了二分，其实可以很容易想到倍增。你从某个盘子开始，照理来说是会跳到下一个可以跳滴盘子，但是如果想要优化时间，可以多跳！对，这就是倍增，跳 $2$ 的幂次。于是我们可以用ST表维护 $nxt[i][j]$ （从盘子 $i$ 往后跳 $2^j$ 步到达的盘子编号）和 $sum[i][j]$ 区间总水量。

可以写出下面的处理代码：

void pre_rmq(){
	for(ri j=1;(1<<j)<=n;j++){
		for(ri i=1;i+(1<<j)<=n;i++){
			nxt[i][j]=nxt[nxt[i][j-1]][j-1];
			sum[i][j]=sum[i][j-1]+sum[nxt[i][j-1]][j-1];
		}
	}
}

int query(int r,int val){
	if(c[r]>=val){
		return r;
	}
	val-=c[r];
	for(ri i=18;i>=0;i--){
		if(nxt[r][i]!=0&&val>sum[r][i]){
			val-=sum[r][i];
			r=nxt[r][i];
		}
	}
	return nxt[r][0];
}

于是这道题差不多就解决了！

Part 3 完整代码

#include<bits/stdc++.h>
#define ll long long
#define ri register int
using namespace std;
const int MAXN=1e5+10;
int n,q,d[MAXN],c[MAXN],r,v,b[MAXN],nxt[MAXN][20],sum[MAXN][20];
stack <int> stk;

void find_max(){
	for(ri i=1;i<=n;i++){
		while(stk.empty()==0&&d[i]>d[stk.top()]){
			nxt[stk.top()][0]=i;
			sum[stk.top()][0]=c[i];
			stk.pop();
		}
		stk.push(i);
	}
	while(stk.empty()==0){
		nxt[stk.top()][0]=0;
		stk.pop();
	}
}

void pre_rmq(){
	for(ri j=1;(1<<j)<=n;j++){
		for(ri i=1;i+(1<<j)<=n;i++){
			nxt[i][j]=nxt[nxt[i][j-1]][j-1];
			sum[i][j]=sum[i][j-1]+sum[nxt[i][j-1]][j-1];
		}
	}
}

int query(int r,int val){
	if(c[r]>=val){
		return r;
	}
	val-=c[r];
	for(ri i=18;i>=0;i--){
		if(nxt[r][i]!=0&&val>sum[r][i]){
			val-=sum[r][i];
			r=nxt[r][i];
		}
	}
	return nxt[r][0];
}

int main() {
	scanf("%d%d",&n,&q);
	for(ri i=1;i<=n;i++)scanf("%d%d",&d[i],&c[i]);
	memset(sum,0x3f,sizeof(sum));
	find_max();
	pre_rmq();
	for(ri i=1;i<=q;i++){
		scanf("%d%d",&r,&v);
		printf("%d\n",query(r,v));
	}
	return 0;
}

总结一下，做题的思路要讲究循序渐进，慢慢来，不要轻视简单基础的算法和思路！