自动搬运

查看原文

来自洛谷，原作者为

	wjyppm1403 我一直在试图撼动着 我曾要攀登的巍然山峦

搬运于2025-08-24 22:27:12，当前版本为作者最后更新于2025-08-20 09:58:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

可能更好的阅读体验

这是困难的，但也是好的。

原命题叽里咕噜可以转化为树上路径问题。有起点和终点不固定，每经过一个点就可以置反当前状态，问最短路径使得所有状态为 $1$。

显然考虑 DP，首先考虑枚举法确定我们路径的起始点，令我们枚举的点为 $rt$。那么将这个枚举的点 $rt$ 作为有根树提起来。然后考虑如何在这个有根树上进行 DP。考虑一条路径会有如下两种情况：

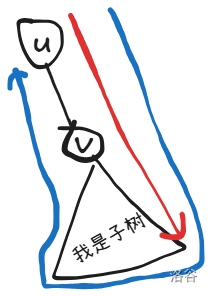
一个直下，一个绕一圈在回来（南下和北上）。考虑 DP 状态中我们需要融入这个状态，设 $f(u,0/1,0/1)$ 表示 $u$ 子树内都为 $1$，是否返回 $u$ 点，当前最终状态是 $0/1$ 的最短路径答案。

转移不太好直接转移，考虑合并子树答案，以下令 $tmp$ 为转移临时存储更新后答案的数组，$\oplus$ 运算代表异或，转移考虑枚举最终状态 $d$，以下转移按顺序进行：

$$tmp(0,d)\leftarrow \begin{cases} 2+\min\{f(u,0,d\oplus 1)+f(v,1,0),f(u,0,d)+f(v,1,1)+2\} \\ \\ 1+\min\{f(u,1,d)+f(v,0,0),f(u,1,d\oplus 1)+f(v,0,1)+2\} \end{cases} $$$$tmp(1,d)\leftarrow 2+\min\{ f(u,1,d\oplus1)+f(v,1,0),f(u,1,d)+f(v,1,1)+2 \} $$$$f(u,0/1,d)\leftarrow tmp(0/1,d)$$

以下解释转移方程。根据上面的图，我们有两种路径模式：直下和绕圈返回。贡献我们可以分摊到边的贡献，对于 $tmp(0,d)$ 的第一部分就是在绕圈进行分讨：

• 常数 $2$ 代表回路一条边经过两次，固定贡献。
• $f(u,0,d\oplus 1)+f(v,1,0)$：我们把 $v$ 子树当成一个完整的回路，然后我们将两端连接，由于绕了一圈 $d$ 一开始就是被置反过的，所以为 $d\oplus 1$。
• $f(u,0,d)+f(v,1,1)+2$：依旧是回路，但是 $v$ 这里最终状态变了，因为经过路径会使得 $v$ 被取反两次，为了使得贡献能够匹配上，我们要把内部在做一次回路改奇偶的操作，这个返回使得 $v$ 子树内边经过 $2$ 次。

第二部分是直下：

• 常数 $1$ 代表边经过一次。
• $f(u,1,d)+f(v,0,0)$ 代表 $u$ 需要返回而 $v$ 必须要，我们两部分用路径穿起来即可。
• $f(u,1,d\oplus 1)+f(v,0,1)+2$：同样是穿越，但是我们也要和上面一样来通过做一次改变奇偶性的操作来使得贡献能够匹配上。

对于 $tmp(1,d)$ 的同理，这里不再细说，但是只用分讨回路的情况即可，因为要回到 $u$ 肯定就没有直下啦。

对于合并当子树已经保证全为 $1$ 的时候可以不用合并，对答案无影响。直接做，时间复杂度 $O(n^2)$。但是注意到转移只有和式，可以通过换根 DP 来进行代替枚举法的决策。具体的，我们需要维护一个 $pre,suf$ 表示前缀儿子 $f$ 合并后的数组和后缀 $f$ 合并后的数组，转移利用 $pre$ 和 $suf$ 即可，具体见代码，时间复杂度 $O(n)$ 但有巨大常数难泵，于是荣获本题最差解，比倒数第二还慢 $300$ 毫秒。

总结：枚举法可以帮助我们确定决策，虽然我们可以在后面优化掉，但这是一个优秀的决策确定方式。同时对于树上路径 DP 问题（不要和点分治搞混了）可以考虑枚举起始点，然后通过换根 DP 确定。

注意我们 $pre$ 和 $suf$ 是开在函数内部的，不要瞎开大数组，可以用指针分配内存或 vector 方便一下。

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=5e5+15,INF=0x3f3f3f3f;
int n,ans=INF,a[MN];
vector<int> adj[MN];

namespace Tree{
    int f[MN][2][2];
    bool vis[MN];

    void init(int u){
        vis[u]=a[u];
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                f[u][i][j]=(j!=a[u])?INF:0;
            }
        }
    }

    void merge(int u,int v){
        vis[u]&=vis[v];
        if(vis[v]) return;
        int tmp[2][2]{};
        for(int i=0;i<2;i++){
            tmp[0][i]=min(
                min(f[u][0][i^1]+f[v][1][0],f[u][0][i]+f[v][1][1]+2)+2,
                min(f[u][1][i]+f[v][0][0],f[u][1][i^1]+f[v][0][1]+2)+1
            );
            tmp[1][i]=min(f[u][1][i^1]+f[v][1][0],f[u][1][i]+f[v][1][1]+2)+2;
        }
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                f[u][i][j]=tmp[i][j];
            }
        }
    }

    void dfs1(int u,int pre){
        init(u);
        for(auto v:adj[u]){
            if(v==pre) continue;
            dfs1(v,u);
            merge(u,v);
        }
    }

    void dfs2(int u,int pree){
        int len=adj[u].size();
        vector<array<array<int,2>,2>> pre(len+1),suf(len+1);
        vector<bool> prev(len+1),sufv(len+1);
        init(u);
        for(int i=0;i<len;i++){
            for(int x=0;x<2;x++) for(int y=0;y<2;y++) pre[i][x][y]=f[u][x][y];
            prev[i]=vis[u];
            merge(u,adj[u][i]);
        }
        init(u);
        for(int i=len-1;i>=0;i--){
            for(int x=0;x<2;x++) for(int y=0;y<2;y++) suf[i][x][y]=f[u][x][y];
            sufv[i]=vis[u];
            merge(u,adj[u][i]);
        }
        ans=min(ans,f[u][0][1]);
        for(int i=0;i<len;i++){
            int v=adj[u][i];
            if(v==pree) continue;
            for(int x=0;x<2;x++) for(int y=0;y<2;y++) f[u][x][y]=INF;
            for(int i1=0;i1<2;i1++){
                for(int j1=0;j1<2;j1++){
                    for(int i2=i1^1;i2<2;i2++){
                        for(int j2=0;j2<2;j2++){
                            f[u][i1&i2][j1^j2^a[u]]=min(f[u][i1&i2][j1^j2^a[u]],pre[i][i1][j1]+suf[i][i2][j2]);
                        }
                    }
                }
            }
            vis[u]=prev[i]&sufv[i];
            dfs2(v,u);
        }
    }

}using namespace Tree;

signed main(){
    string st;
    cin>>n>>st;
    st=" "+st;
    for(int i=1;i<=n;i++) a[i]=(st[i]=='1');
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    dfs1(1,0);
    dfs2(1,0);
    cout<<ans<<"\n";
    return 0;
}