自动搬运

查看原文

来自洛谷，原作者为

	Thomas_Cat 越学越菜。

搬运于2025-08-24 22:26:54，当前版本为作者最后更新于2020-11-26 23:36:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

$$\texttt{「RdOI R1」一次函数(function) 官方题解}$$

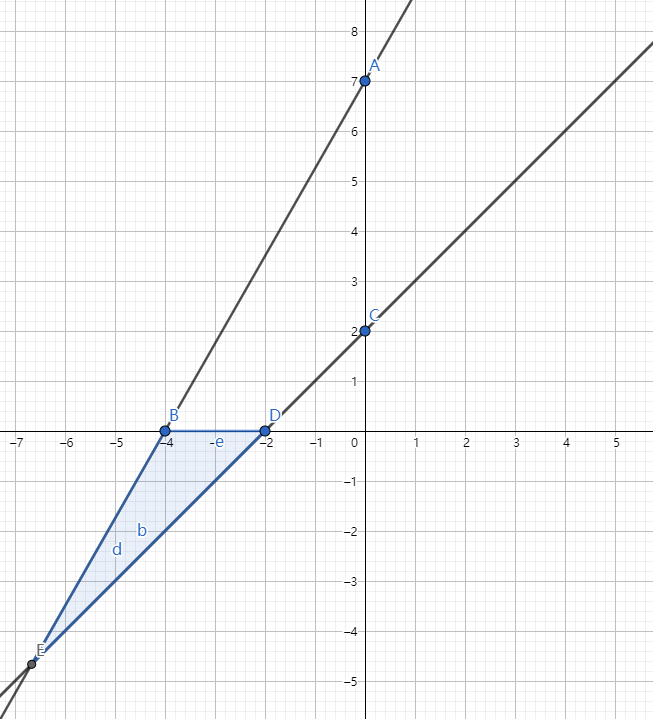
这里为了方便，拟了一个 $l_1,l_2$，仅为参考，阴影部分表示的就是要求的三角形的面积。

对于直线 $l_1,l_2$，我们可以令 $y = 0$，则：

对于 $l_1$：

$$kx+k-1=0$$ $$kx=1-k$$ $$x=\dfrac{1-k}{k}$$

---

对于 $l_2$：

$$(k+1)x+k=0$$ $$(k+1)x=-k$$ $$x=-\dfrac{k}{k+1}$$

则，图像中三角形的底为

$\because \dfrac{1-k}{k}>-\dfrac{k}{k+1}$

$\therefore \dfrac{1-k}{k}-(-\dfrac{k}{k+1})=\dfrac{1}{k(k+1)}$

---

因此我们现在得到一个方程组：

$$\begin{cases}y=kx+k-1\\y=(k+1)x+k\end{cases}$$

则，

$$kx+k-1=(k+1)x+k$$ $$kx+k-1=kx+x+k$$ $$x=-1$$

当 $x=-1$ 时，$y=-1$。

则：$| -1 | = 1$。

则：图像中三角形的高为 $1$。

---

因此我们列出一个方程：

$S_1+S_2+S_3+\cdots+S_n$

$=\dfrac{1}{2} \times 1 \times(\dfrac{1}{1 \times (1+1)}+\dfrac{1}{2 \times (2+1)}+ \cdots +\dfrac{1}{n\times(n+1)})$

裂项后，得：

$=\dfrac{1}{2} \times 1 \times(1-\dfrac{1}{n+1})$

$=\dfrac{1}{2} \times \dfrac{n}{n+1}$

$=\dfrac{n}{2(n+1)}$

---

官方std：

#include<bits/stdc++.h>
using namespace std;
int main(){
	int t;
	scanf("%d", &t);
	while(t--){
		int n;
		scanf("%d", &n);
		if(n==0) puts("0");
		else{
		    int a=n;
		    int b=(n+1)*2;
		    int tmp=__gcd(a,b);
            printf("%d/%d\n", a/tmp, b/tmp);
		}
	}
	return 0;
}