自动搬运

查看原文

来自洛谷，原作者为

	zhylj 人生输家

搬运于2025-08-24 22:26:51，当前版本为作者最后更新于2021-11-03 19:47:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

我们希望用 DFS 搜遍整张图，并模拟类似 Tarjan 的过程，大致有：

• 不妨设 left 标记的点表示被遍历过、且不在栈中的点（此处栈即为 DFS 的栈，而不是 Tarjan 算法中的栈），right 表示栈中的点，center 表示还没访问过的点。
• 我们希望对所有点进行 $m$ 次 1 right 1 来遍历其所有出边。
• 在 DFS 过程中，我们将记录当前点 $u$ 在 DFS 树中的子树中的点能到达的栈中 DFS 序最小的点 $\operatorname {low}_u$ 和当前点的距离 $\operatorname {lowcnt}_u$ 和用于更新 $\operatorname {low}_u$ 所用到的出边 $\operatorname {lowidx}_u$。
• 在退出一个点的时候，我们把标记搬到指向 $\operatorname {low}_u$ 的位置（由于图为强连通图，所以若 $u$ 不是 DFS 树的根，则 $\operatorname {low}_u$ 是 $u$ 的某个祖先）。

更具体地，我们分别考虑当前点 $u$ 走过某个通道到达了 $v$ 为三种点的情况：

• 若 $v$ 为 center，则递归处理 $v$，然后用 $\operatorname{lowcnt}_v-1$ 更新 $\operatorname {lowcnt}_u$。
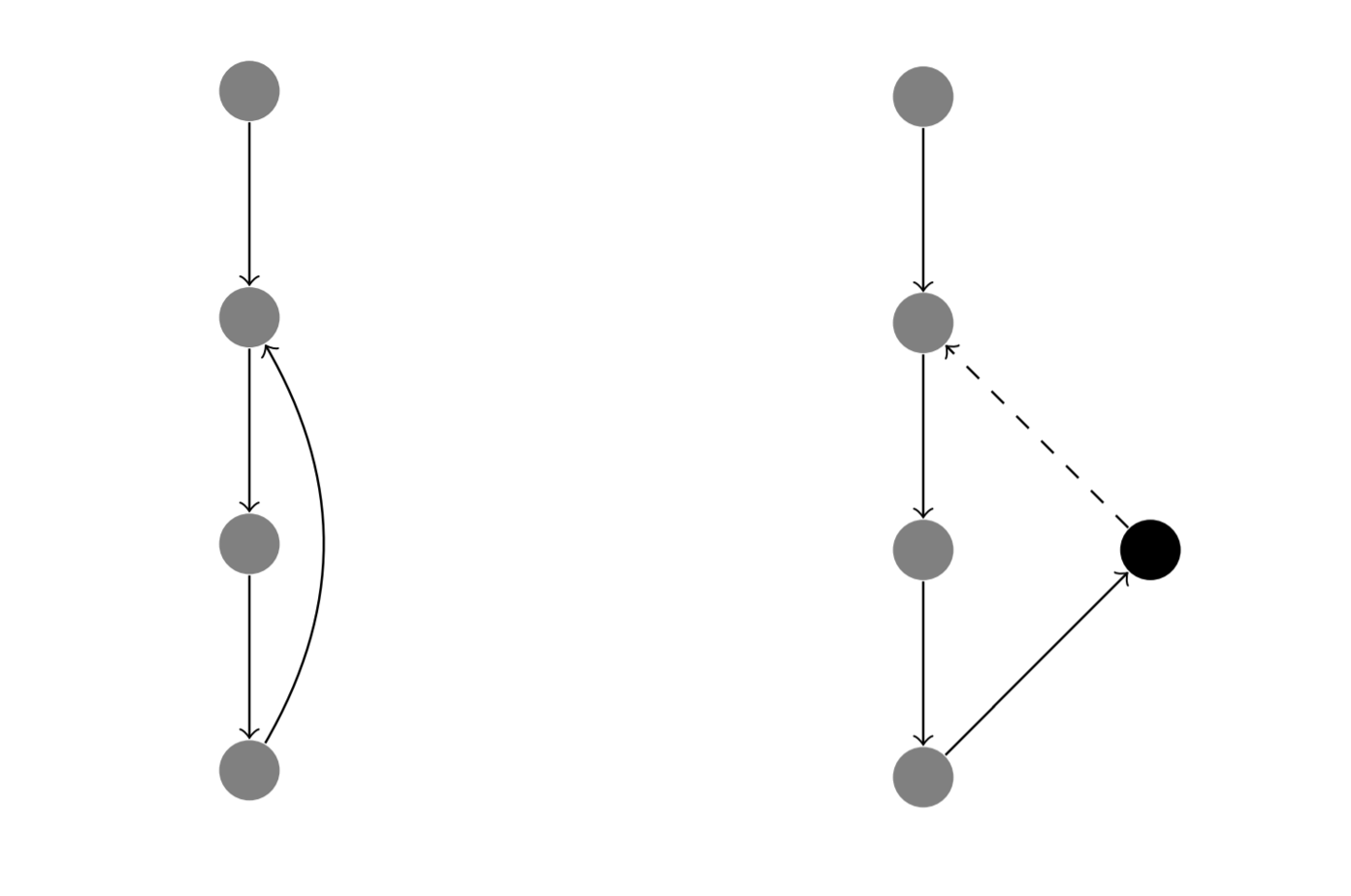
• 若 $v$ 为 right，则意味着我们走到了一个返祖边（如下图左）：
  • 从 $v$ 开始，先进行一次 0 left 0，临时标记一下当前点（此时的 left 意义与上面定义的不同，只是为了区分栈中的节点，之后将很快被改回去）。
  • 接下来进行若干次 0 right 0 顺着原先走过的路径走，直到遇见被标为 left 的 $v$，并记录这部分的边数 $c$。
  • 接下来再进行 $c$ 次 0 right 0，于是我们在返回 $u$ 的同时顺带把 $v$ 给改回了 right。
  • 用 $c$ 更新 $\operatorname {lowcnt}_u$，当前边更新 $\operatorname {lowidx}_u$。
• 若 $v$ 为 left，则意味着我们走到了一个已经访问过了的点（如下图右），我们希望退回到 $u$。
  • 若当前遇到的节点一直是 left，则一直进行 0 left 0。
  • 然后我们总会找到一个 right，之后一直进行 0 right 0 找到第一个 left 即为 $v$，记录这部分的边数 $c$。
  • 不难通过类似方法再走一圈，但少一条边走回 $u$。
  • 用 $c-1$ 更新 $\operatorname {lowcnt}_u$，当前边更新 $\operatorname {lowidx}_u$。

在一个点所有 $m$ 条出边都被访问完之后，我们要回溯到其父亲，考虑利用先前算过的 $\operatorname {low}_u$ 做到“返祖”：

• 先将本身设为 left，然后走到 $\operatorname{lowidx}_u$。
• 不断的做 0 left 0，直到遇见一个 right 节点，显然其为 $\operatorname {low}_u$。
• 再往下走 $\operatorname{lowcnt}_u-1$ 步即可走到 $u$ 的父亲。

然后就完成了 DFS 的过程，注意到每条边我们可能需要走 $2n$ 步，总共 $nm$ 条边，所以至多走 $2n^2m=16000$ 步，可以通过本题。

const int INF = 0x3f3f3f3f;

char str[2][10] = { "left", "right" }, buf[10];
char Pass(int a, char typ, int b) {
	printf("%d %s %d\n", a, str[typ == 'l' ? 0 : 1], b);
	fflush(stdout);
	scanf("%s", buf);
	if(buf[0] == 't') exit(0);
	return buf[0];
}
int Walk(char typ, int x = INF) {
	char cur = typ; int ret = 0;
	for(; cur == typ && ret < x; ++ret) cur = Pass(0, typ, 0);
	return ret;
}

int m, dfv, low_c[30];
int Dfs() {
	int u = ++dfv, low_idx = -1;
	for(int i = 0; i < m; ++i) {
		char ret = Pass(1, 'r', 1);
		int c = 0;
		if(ret == 'c') {
			int v = Dfs();
			c = low_c[v] - 1;
		} else if(ret == 'r') {
			if(Pass(0, 'l', 0) == 'r') {
				c = Walk('r'); Walk('r', c);
			} else {
				c = 0; Pass(0, 'r', 0);
			}
		} else if(ret == 'l') {
			Walk('l'); c = Walk('r') - 1;
			Walk('l'); Walk('r', c);
		}
		if(c > low_c[u]) {
			low_idx = (i + 1) % m;
			low_c[u] = c;
		}
	}
	if(u != 1) {
		char cur = Pass(low_idx, 'l', low_idx);
		if(cur == 'l') Walk('l');
		Walk('r', low_c[u] - 1);
	}
	return u;
}

int main() {
	scanf("%d%s", &m, buf);
	Dfs();
	return 0;
}