自动搬运

查看原文

来自洛谷，原作者为

	泥土笨笨 《算法竞赛实战笔记》作者

搬运于2025-08-24 22:26:46，当前版本为作者最后更新于2021-02-16 15:35:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

我有个梦想，我想写一篇多图的，讲解细的，注释多的，$O(nlog26)$复杂度的题解。

前置知识

1. 树状数组 这个相信能参加NOIP的同学都会。
2. 扩展KMP算法 模板题：P5410 【模板】扩展 KMP（Z 函数） 这道题我也写了题解，欢迎评论点赞围观。这道模板题是紫色的，其实一点也不难，我觉得难度有点虚标了，相信你看了我的题解很快就可以学会的。

如果你不会扩展KMP算法，其实也不影响你阅读本文，只需知道这个算法提供了一个z函数的计算方式。

不妨设输入的字符串是$s$，下标从$0$开始，长度是$n$。用$s[i,j]$表示$s$中从下标$i$位置到下标$j$位置的子串，包括$i$和$j$。那么$z[i]$表示$s[i,n-1]$与$s$本身的最长公共前缀的长度。

比如$z[0]$表示$s$与$s$的公共子串的长度，那么$z[0]=n$

$z[1]$表示$s$去掉开头第一个字符以后，和自己的最长公共前缀的长度，依次类推。扩展KMP算法可以在$O(n)$时间内求出$z$数组的所有位置。

枚举循环节长度

先不考虑题中的出现奇数次这个条件。先考虑把$s$拆成$(AB)^kC$的方案数，其中$AB$合起来是一个循环节，我们先考虑一个循环节有多长。

不妨设循环节长度为$i$，第一个发现是，只要满足$2 \leq i \leq n-1$都可以。因为$A$和$B$都不能为空，所以循环节长度至少是$2$。循环节长度最多是$n-1$，因为$C$也不能为空。

当循环节长度是$i$的时候，至少$k$可以取到$1$，就是只循环一次，后面剩下的都给$C$。除此之外，k还可以取多少呢？不妨以$i=3$为例，画一个图看看

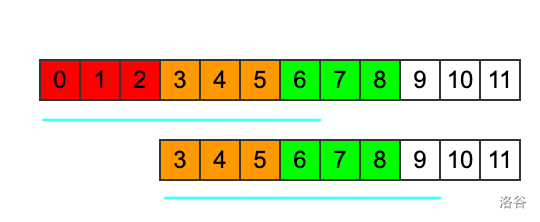
假设$z[3]=7$，也就是说，字符串从$3$位置开始，连续$7$个长度的子串，和字符串刚开头的$7$个字符相等。那么我们把$s$再画一遍，去掉前$3$个位置，抄在下面，如图所示，那么画蓝线的部分是相等的。

现在考虑长度为$3$的循环节，首先红色的$3$个位置，和下面橙色的三个位置肯定是相等的，因为它们都是蓝线部分开头的$3$个。而橙色的部分上下是对应相等的，于是红色和橙色相等。

同理，由于橙色和绿色相等，那么红，橙，绿都相等，也就是说长度为3的循环节，至少可以循环3次。这里可以看出，蓝线的长度，除以循环节的长度再加1，就可以算出来最多可以循环几次，如果不能整除，向下取整。这个例子里面就是$\lfloor 7/3 \rfloor +1$，那么$k$可以取$3$种。

那么第一个结论就出来了，枚举一下循环节的长度i，总的方案数就是

$$\lfloor \frac{z[i]}{i} \rfloor +1$$

之和。

考虑字符出现的次数

题目中还有一个条件我们没有考虑，为了说话方便，我们定义$f(i,j)$表示$s[i,j]$中出现奇数次的字符的个数。

假设现在枚举到循环节长度为$i$，此时根据前面的结论，我们算出来$k$的方案数有$t$种。其中一半$k$是奇数，一半$k$是偶数。当然奇数可能比偶数多一个。不妨设$k$是奇数的取值方案数是$tj$，那么有$tj = t-t/2$，同理设偶数的$k$的个数是$to$，有$to = t/2$

考虑$k$的取值。如果$k$的值是奇数:

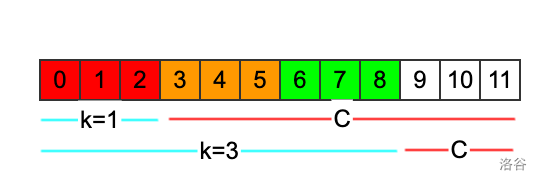
如图所示，$k=1$时候，$C$的长度是从$i$开头的后缀的长度。$k=3$的时候，$C$是更短的红线表示的范围。这两种情况下，$C$当中出现次数为奇数的字符的个数是一样多的，因为如果循环节多出现了两次，相当于循环节里面的每个字符都出现了偶数次，不影响$C$当中出现次数为奇数次的字符的个数。

所以，当$k$是奇数的时候，我们只需计算出来，以$i$为开头的后缀当中出现奇数次的字符的个数就行了。然后在长度为i的子串的前缀$s[0,j]$当中，找出来满足：

$$f(0,j) \leq f(i,n-1)$$

的$j$的个数，记为$t1$。而对于每个合法的$j$，我们发现，只要是奇数的$k$，都可以是一种合法方案，所以这里要乘法原理一下，把$t1$和$tj$的个数相乘。

再来考虑k是偶数的情况。

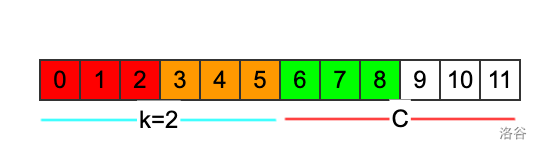
跟前面情况类似，当k是偶数的时候，后缀C里面的只出现奇数次的字符的个数，和整个串里面只出现奇数次的字符个数是相等的。在长度为i的子串的前缀$s[0,j]$当中，找出来满足：

$$f(0,j) \leq f(0,n-1)$$

的$j$的个数，记为$t2$。那么这种情况下的方案数，就是$t2$和$to$相乘。

具体实现

首先前面的算法中用到了$f(0,n-1)$，这个好办，直接预处理算出来就行了。

在从左往右扫字符串$s$的过程中，假设我们目前枚举到位置$i$，此时我们计算循环节长度为$i+1$的情况，此时$A$最远可以取到$i-1$位置，把$i$位置留着给$B$，保证$B$不为空。我们可以用一个桶，维护$i+1$开头的后缀里面每个字母出现的次数，当$i$向右循环的时候，每次只改一个字符，所以在桶的对应位置减$1$，然后看看出现奇数次的字符数量如何变化就行了。

不妨设这个桶叫$after$，一共有$26$个格，分别表示每个字符出现的次数。起始的时候，先扫一遍s，把整个字符串都统计一遍，这时候可以顺手求出整个串里面只出现奇数次的字符的个数，记到$all$变量里面。然后当后面循环的时候，循环到$i$位置，就把$after[s[i]-'a']$位置减$1$。设变量$suf$表示$f[i+1,n-1]$，如果在$after[s[i]-'a']$减1之前，$suf$是奇数，那么减完以后，后缀里面的奇数就会少一个，那么$suf$减$1$，否则$suf$加一。这样每次$i$移动，$suf$都可以$O(1)$维护。

那么循环节里面的每个前缀中出现奇数次的字符个数，可以放到一个树状数组里面，这样这个树状数组一共有$26$个位置，每个位置$p$保存出现奇数次的字符有$p$个的前缀有多少个。$i$每向右循环$1$位，就在计算完结果以后，把当前前缀扔到树状数组里面。

其他细节可以参考代码

代码时间

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
const int MAXN = (1 << 20) + 5;
char s[MAXN];//输入的字符串
int n, z[MAXN];//字符串长度，以及z函数的值
int before[30], after[30];//两个桶，分别统计当前枚举到的位置左侧和右侧每个字符出现的频次
int pre, suf, all;//当前枚举到的位置的前缀、后缀、整个串里面出现奇数次的字符的个数

//树状数组，对于s的某个前缀si，如果它里面出现奇数次的字符有m个，则在树状数组m+1位置+1
int c[30];

inline int lbt(int x) {
    return x & -x;
}

void update(int x) {
    while (x <= 27) {
        c[x]++;
        x += lbt(x);
    }
}

int sum(int x) {
    int r = 0;
    while (x > 0) {
        r += c[x];
        x -= lbt(x);
    }
    return r;
}

//扩展KMP算法，计算z函数的值
//可以参考良心博客 https://www.luogu.com.cn/blog/nitubenben/solution-p5410
void Z() {
    z[0] = n;
    int now = 0;
    while (now + 1 < n && s[now] == s[now + 1]) {
        now++;
    }
    z[1] = now;
    int p0 = 1;
    for (int i = 2; i < n; ++i) {
        if (i + z[i - p0] < p0 + z[p0]) {
            z[i] = z[i - p0];
        } else {
            now = p0 + z[p0] - i;
            now = max(now, 0);
            while (now + i < n && s[now] == s[now + i]) {
                now++;
            }
            z[i] = now;
            p0 = i;
        }
    }
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> s;
        n = strlen(s);
        memset(before, 0, sizeof(before));
        memset(after, 0, sizeof(after));
        memset(c, 0, sizeof(c));
        all = pre = suf = 0;
        Z();
        //如果发现循环节可以到结尾，减1，空至少一个位置给C
        for (int i = 0; i < n; ++i) {
            if (i + z[i] == n) z[i]--;
        }
        //先把字符串过一遍，频次统计到after数组里面
        for (int i = 0; i < n; ++i) {
            after[s[i] - 'a']++;
        }
        //扫一下每个字母，计算整个串中出现奇数次的字符的个数
        for (int i = 0; i < 26; ++i) {
            if (after[i] & 1) {
                all++;
            }
        }
        suf = all;//后缀中的值暂时和整个串一致
        long long ans = 0;
        for (int i = 0; i < n; ++i) {
            //再扫一次字符串，当循环到i位置的时候，循环节长度是i+1
            //s[i]要从右边去掉，维护after数组和suf变量
            if (after[s[i] - 'a'] & 1) {
                //之前是奇数，现在变成偶数了
                suf--;
            } else {
                suf++;
            }
            after[s[i] - 'a']--;
            //s[i]加到左边，维护before和pre变量
            if (before[s[i] - 'a'] & 1) {
                pre--;
            } else {
                pre++;
            }
            before[s[i] - 'a']++;
            if (i != 0 && i != n - 1) {
                //循环节大于1,才能对答案有贡献，因为题中说ABC都不为空
                int t = z[i + 1] / (i + 1) + 1;
                ans += 1LL * (t / 2) * sum(all + 1) + 1LL * (t - t / 2) * sum(suf + 1);
            }
            update(pre + 1);
        }
        cout << ans << endl;
    }
    return 0;
}