自动搬运

查看原文

来自洛谷，原作者为

	BFqwq 青く广がった あの空のように、昙りなく笑えたら あなたに会いたい。

搬运于2025-08-24 22:26:43，当前版本为作者最后更新于2020-12-01 23:03:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P7110 【晚秋绝诗】

先膜一发 sooke。

在月赛的时候我跳过了 T4，直接来开这道题，结果是因为各种浪费时间/评测机罢工导致我最后没能 AC（最后只有 jiangly 一个人过了）。

在赛后我听了 sooke 的讲评，并对我的做法进行了一点优化，于是就有了你们所看到的这篇题解。

首先，我们需要研究一下什么样的点是可以被测出高度的。

在如果这个点是已知的，那么它显然可以被测出。如果是未知的，那我们就需要依靠一些旗子的信息。

引理：对于若干座连着插旗的山，以及与这几座山相邻的未插旗的两座山，只要它们中有两座山能被测出，则这些山全部能被测出。

比如这张图：

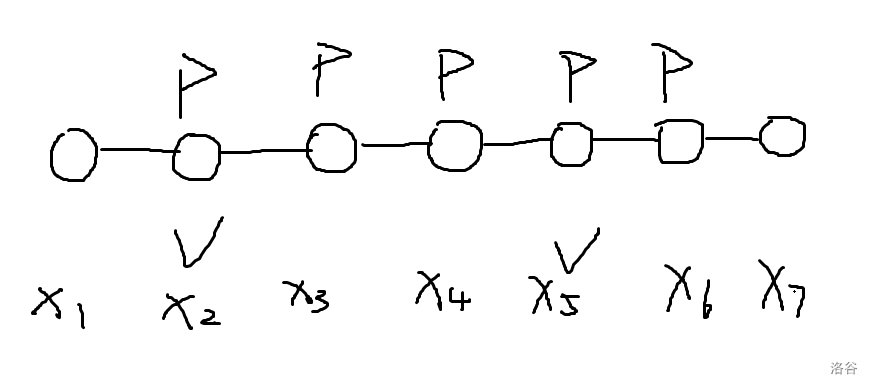
目前 $x_2,x_5$ 已知，并且 $x_2$ 到 $x_6$ 都插着旗，则我们一定可以推出 $x_1$ 到 $x_7$ 中的所有数。

因为我们首先可以列出两个式子：

$$x_2+x_4=2\times x_3$$ $$x_3+x_5=2\times x_4$$

其中 $x_2,x_5$ 已知。然后你会发现这就是一个一元二次方程组，并且是可以解的。于是我们就确定了中间的所有数。

然后我们根据 $x_3-x_2=x_2-x_1$ 可以推出 $x_1$，同理推出 $x_6,x_7$，因此证明了可行性。

但有人会问，如果中间不是两个，而是三个，四个……能解吗？

答案是可以。因为一元方程的数量比与未知数相同，并且没有构成循环之类的情况，那么方程就是有解的。

带着这个结论，我们继续思考。

我们称相邻的两个不插旗的节点与中间的若干个插旗的节点为一个段，其中这两个未插旗的点我们称为端点。

刚才我们说明了，在一个段中，知二求全。但现在的问题是，我们已知的这两个点不一定是从本段中出来的，可能是由边上的段传递过来的。

比如我们已知 $x_1,x_4,x_5$，然后又知道 $2,4$ 两点插旗。那我们可以通过 $x_4,x_5$ 求出 $x_3$，然后通过 $x_1,x_3$ 求出 $x_2$。

于是这个题就变得复杂了起来。我在比赛的时候也就是因为这里的处理一直没有调出来。

但随后我们又发现，对于传进来的值，一定是出现在段的端点处的。

那么对于一个子段，我们它可能存在四种情况：

1. 有两个及更多的已知点；

2. 有一个已知点且已知点在端点（不插旗）；

3. 有一个已知点且已知点不是端点（插旗）；

4. 没有已知点。

对于第一类的子段上的点，显然我们可以直接确定它是可以求出。同时，它还可以为两边的子段提供已知点，就好像一个信号发射器。

对于第四类的子段上的点，显然我们需要两边都收到一个已知点能确定其上面的所有值。同时，对于任意一边提供的已知点，它都不可以将它传递到其他另一端（因为求不出另一端的值），就好像一个信号阻隔器。

对于第三类的子段上的点，只要左右任意一个端点给出一个已知点，我们就能确定其上面的所有值。同时，对于任意一端给出的已知点，我们可以通过这一信息求出另一端的值，从而为另一端提供已知点，就好像一个信号传递器。

对于第二类子段上的点，已经有一个端点是已知点了。那么我们如果想要求出它上面的点，我们就需要再来一个已知点，而这个已知点就只能是另一个端点。相当于我们需要从另一个端点收到一个已知点，可以认为是单向的信号发射器。

然后我们考虑维护所有的段。这里可以使用一个 $set$。

对于操作 $1$，我们求出这个点所在的段（注意可能同时在两个段），然后分别重新求一次其类型即可。

对于操作 $2$，我们找到其对应的段，然后将段对应合并/分裂并求出其类型即可。

然后问题就是操作 $3$，我们如何判断是否可行。

要判断是否可行，我们需要知道它左右的段能否为其提供已知点。

对于左右是第 $1,2,4$ 种段的情况，非常方便。但问题是存在 $3$ 这样的段，需要继续遍历，可能会导致复杂度的增高。

于是我们可以再使用一个 $set$ 来进行维护。对于能提供已知点的点，我们在 $set$ 的对应位置插入 $1$，能阻隔已知点传递的点，我们则插入 $0$。

对于 $3$ 类段这种仅供传递的，我们直接不管。

然后我们只需要查询 $set$ 中左右最近的点是 $1$ 还是 $0$ 就好了。

（这个跳过第三类段的方法是 sooke 神仙的题解中提到的，比我当时写的东西简单许多，所以在这里我当时的写法就不讲了）

然后就是一些细节性的东西，比如左右插入防越界的段云云。因为大部分都是以 $STL$ 为主，所以细节挺多的，不仔细就容易错。

#include<bits/stdc++.h>
#define lb(o) lower_bound({o,-1})
using namespace std;
inline int read(){
	register int x=0;
	register bool f=0;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-48;
		ch=getchar();
	}
	return f?-x:x;
} 
char str[300];int kkk;
inline void print(register int x,register char k='\n'){
	if(!x) putchar('0');
	if(x<0) putchar('-'),x=-x;
	while(x){
		str[++kkk]=x%10+48;
		x/=10;
	}
	while(kkk){
		putchar(str[kkk--]);
	}
	putchar(k); 
}
bool a[500100],b[500100];
int n,m,s[500100<<2];
void change(int o,int l,int r,int q){
    if(l==r){
        s[o]=a[l];
        return;
    }
    int mid=l+r>>1;
    if(q<=mid) change(o<<1,l,mid,q);
    else change(o<<1|1,mid+1,r,q);
    s[o]=s[o<<1]+s[o<<1|1];
}
int query(int o,int l,int r,int ql,int qr){
	if(ql==0||qr==n+1){
		return 0;
	}
	if(ql<=l&&r<=qr){
		return s[o];
	}
	int mid=l+r>>1;int ans=0;
	if(ql<=mid) ans+=query(o<<1,l,mid,ql,qr);
	if(qr>mid) ans+=query(o<<1|1,mid+1,r,ql,qr);
	return ans;
}
struct node{
	int l,r,c;
	friend bool operator <(node a,node b){
		return a.l==b.l?a.r<b.r:a.l<b.l;
	}
}tmp;
struct pos{
	int o,v;
	friend bool operator <(pos a,pos b){
		return a.o==b.o?a.v<b.v:a.o<b.o;
	}
}t;
set<node> st;
set<pos> val;
set<node>::iterator it;
set<pos>::iterator it2;
void ins(node p){
	int l=p.l,r=p.r;
	int v=query(1,0,n+1,l,r);
	if(v>=2){
		p.c=1;t.v=1;
		st.insert(p);
		t.o=l*2+1;
		val.insert(t);
		t.o=r*2;
		val.insert(t);
	}
	if(v==0){
		p.c=4;t.v=0;
		st.insert(p);
		t.o=l*2+1;
		val.insert(t);
		t.o=r*2;
		val.insert(t);
	}
	if(v==1){
		if(!a[l]&&!a[r]){
			p.c=3;
			st.insert(p);
		}
		else{
			p.c=2;
			st.insert(p);
			t.o=l*2+1;t.v=a[l];
			val.insert(t);
			t.o=r*2;t.v=a[r];
			val.insert(t);
		}
	}
}
void del(node p){
	st.erase(p);
	if(p.c!=3){
		it2=val.lb(p.l*2+1);
		val.erase(it2);
		it2=val.lb(p.r*2);
		val.erase(it2);
	}
}
bool get(node p){
	if(p.c==1) return 1;
	if(p.c==2){
		if(a[p.l]){
			it2=val.lb(p.r*2+1);
			return it2->v;
		}
		else{
			it2=val.lb(p.l*2+1);it2--;
			return it2->v;
		}
	}
	if(p.c==3){
		it2=val.lb(p.r*2+1);t=*it2;
		it2=val.lb(p.l*2+1);it2--;
		return it2->v|t.v;
	}
	if(p.c==4){
		it2=val.lb(p.r*2+1);t=*it2;
		it2=val.lb(p.l*2+1);it2--;
		return it2->v&t.v;
	}
}
void change(int o){
	a[o]^=1;
	change(1,0,n+1,o);
	if(b[o]){
		tmp.l=o;tmp.r=0;
		it=st.upper_bound(tmp);it--;
		tmp=*it;
		del(tmp);
		ins(tmp);
	}
	else{
		tmp.l=o;tmp.r=0;
		it=st.lower_bound(tmp);
		tmp=*it;
		it--;
		node tmp2=*it;
		del(tmp2);ins(tmp2);
		del(tmp);ins(tmp);
	}
}
void update(int o){
	if(b[o]){
		b[o]=0;tmp.l=o,tmp.r=0;
		it=st.upper_bound(tmp);it--;
		tmp=*it;del(tmp);
		node tmp2;tmp2.l=tmp.l;
		tmp2.r=tmp.l=o;
		ins(tmp2);ins(tmp);
	}
	else{
		b[o]=1;tmp.l=o,tmp.r=0;
		it=st.lower_bound(tmp);tmp=*it;
		it--;node tmp2=*it;
		del(tmp2);del(tmp);
		tmp.l=tmp2.l;
		ins(tmp);
	}
}
void query(int o){
	if(a[o]){
		print(1);
		return;
	}
	if(b[o]){
		tmp.l=o;tmp.r=0;
		it=st.upper_bound(tmp);
		it--;tmp=*it;
		print(get(tmp));
	}
	else{
		tmp.l=o;tmp.r=0;
		it=st.lower_bound(tmp);
		tmp=*it;it--;
		print(get(tmp)|get(*it));
	}
}
signed main(){
//	freopen("1.in","r",stdin);
//	freopen("1.out","w",stdout); 
	n=read();m=read();
	for(int i=0;i<=n;i++){
		tmp.l=i;tmp.r=i+1;tmp.c=4;
		st.insert(tmp);
		t.o=i*2+1;t.v=0;
		val.insert(t);
		t.o=(i+1)*2;
		val.insert(t);
	}
	st.insert(tmp);
	tmp.l=n;tmp.r=n+1;tmp.c=4;
	st.insert(tmp);int cnt;
	for(int i=1;i<=m;i++){
		int opt=read();
		if(opt==1){
			change(read());
		}
		if(opt==2){
			update(read());
		}
		if(opt==3){
			query(read());
		}
	}
	return 0;
}