1 条题解
-
0
自动搬运
来自洛谷,原作者为

AsunderSquall
The cruelest fate is to have hope and see it crushed before your eyes.搬运于
2025-08-24 22:26:42,当前版本为作者最后更新于2020-11-28 19:36:57,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
刚推出式子时不知道为什么被卡常了,非常自闭 link
声明1:下文由于本人菜,分不清“结点”和“节点”,请忽略。
update:修改了一个笔误。
题意
有一个高度无限的有根满 叉树,你每次操作可以选择一棵子树全部删除,或者选择一棵子树,拼到另一个结点下面,问至少需要几次操作可以把这棵树变成高度为的满叉树。
(题意中有描述的不到位的地方,仅供回忆题目,具体见原题目题解
声明2:下文所说的“删除结点”为删除结点及其子树。
也就是说删得只剩根节点,输出 即可
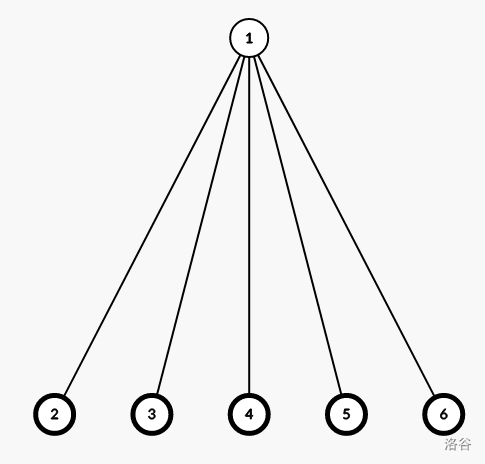
如图为 的情况,删去黑色节点。
if (h==0) cout<<(a);
只需要将多余的子树删去即可
设根为第层,那么要保留到第 层, 层的所有结点都要删去,而第 层有 个结点
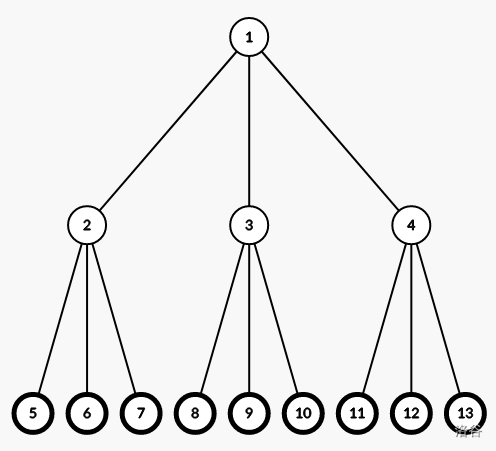
如图为 的情况,删去黑色节点。
if (a==b) cout<<(ksm(a,h+1,mod));
原始的树为一条链
那么我们可以把满 叉树分成若干条从上到下链,使数量最少,链的条数就是答案。
设层的满叉树的链的条数为 。
我们考虑使一棵满 叉树分成的链最少,根节点一定在某条链中,那我们任取一个儿子 ,把经过的链拼上一条 的边。
那么有 又有 ,所以。 以为例
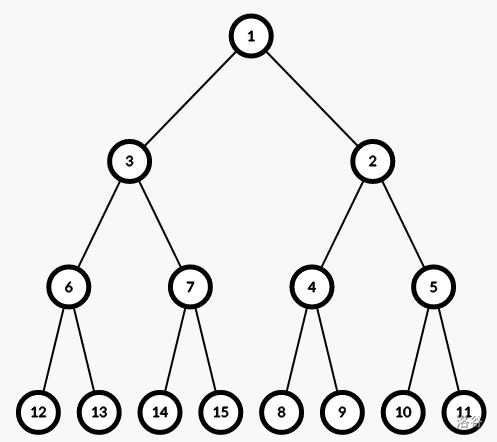
对于根的每个儿子,都可以分成 条链,总共 条链
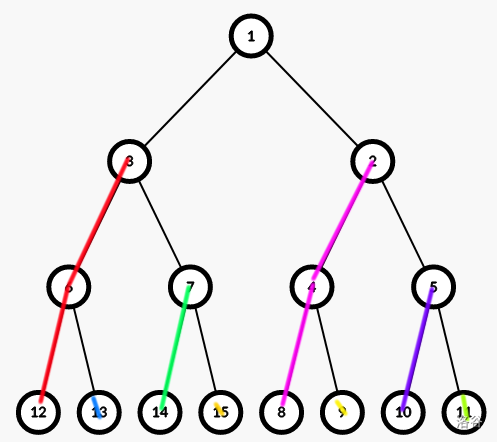
考虑根,只要连到一条经过儿子的链上就行了
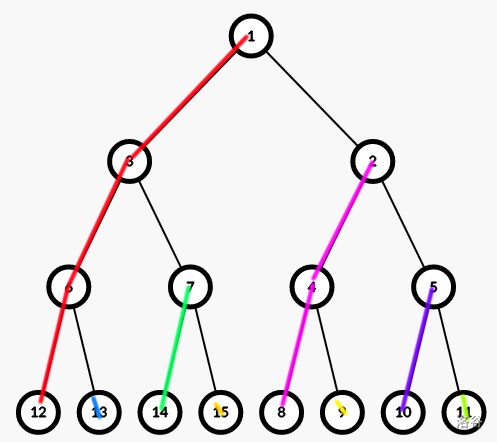
if (a==1) cout<<(ksm(b,h,mod));
要把树删得只剩一条链
那么第 层都有多余的 个结点,而第 层则有 个,将他们删除即可。
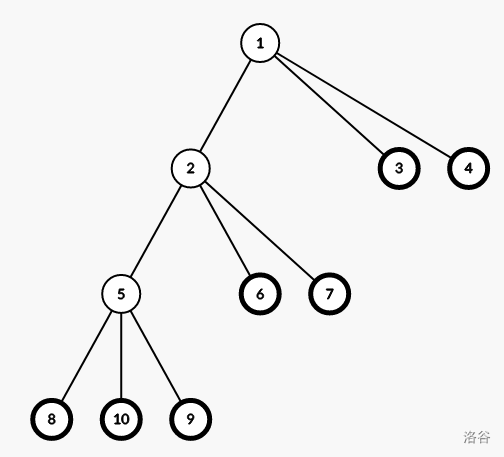
如图为 的情况,删去黑色节点。
if (b==1) cout<<(((a-1)*h+a)%mod);
我感觉后面的点都没什么用……其实只要把这个式子搞出来后面就一样了。。。分为 和 两种情况讨论(因为本人很菜)
我们要把满叉树补成满 叉树
那么我们分为两个步骤- 把前面层补成满叉树
- 删去第层多余的结点
对于第一步,我们考虑一层一层拖子树。
先把第层补完,拖来了 棵子树。
这个时候第层就有 棵子树要拖。
第层有 棵子树要拖。
那么我们只需要将他们加起来 。
对于第二步,第 层有 个结点,那么第 层有 棵子树,将他们全部删去。
所以答案为 。真 的 吗 ?
显然,如果我们将本来第二步中应该删去的子树给拖走,那么就省去了删除这个结点这一步骤。
所以答案为这样说可能有点模糊,我们来举个例子。
Example: (深度 的节点不画出)。
下面的图的标号和上面 出现什么标什么 的标号不太一样,对于标号为 的节点,我们给它的左儿子和右儿子分别标号为 和 。
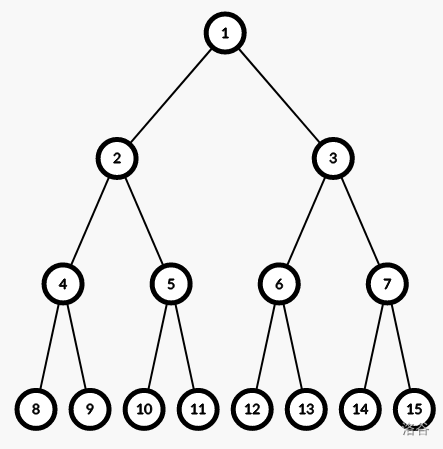
比如说第一层,如果我们随便拖一个下面的节点过来,这样是可行的,但是不够优秀。
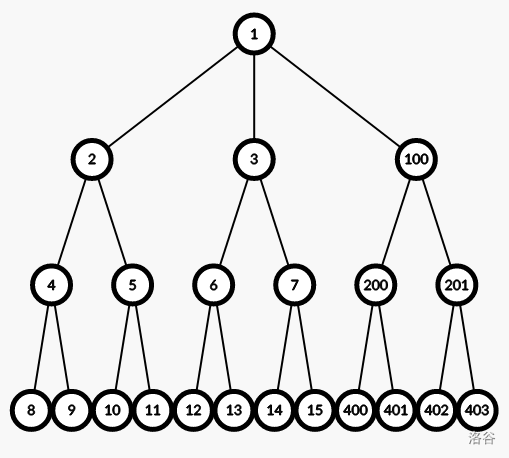
我们知道,到时候我们肯定要把 这个节点从 的儿子中移除,所以我们如果把 拖过来,就可以减少操作次数。
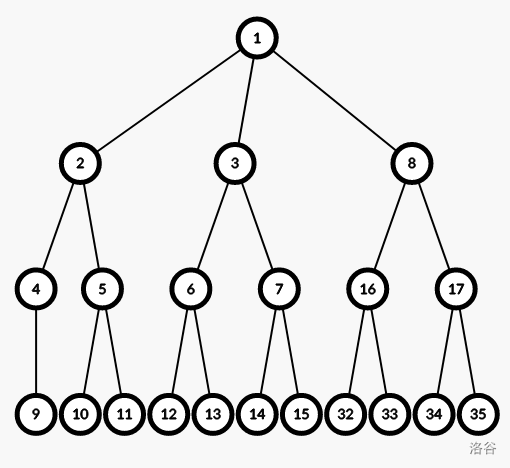
同理,要使 的儿子数目变成 ,我们把 号节点拖过去。
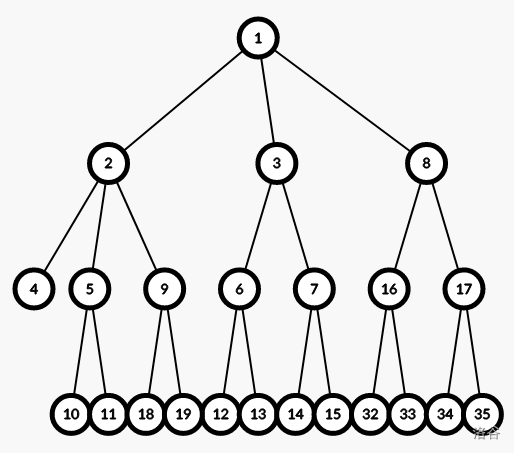
然后
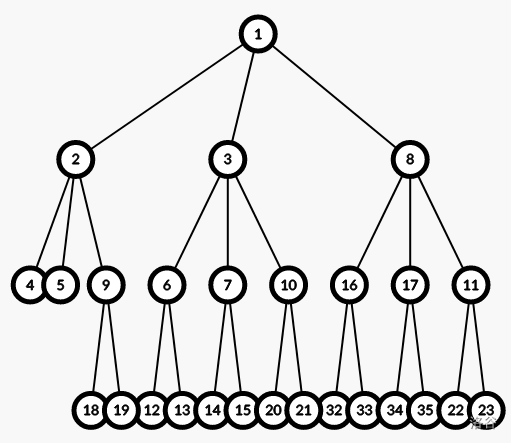
最后把底部的所有节点全部删去
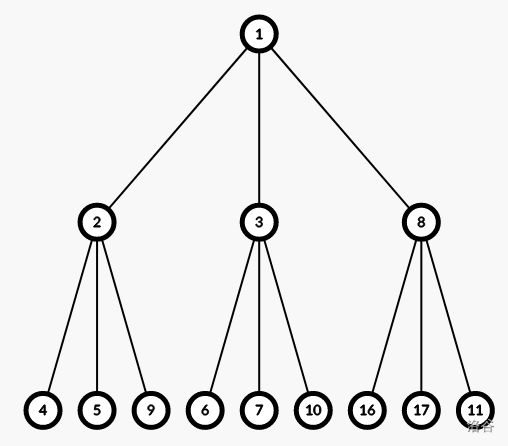
同样分为两个步骤- 把前面层删成满叉树
- 删去第层多余的结点
对于第一步,我们考虑一层一层删子树,答案与 的情况类似,为
对于第二步,为 ,那么答案就为
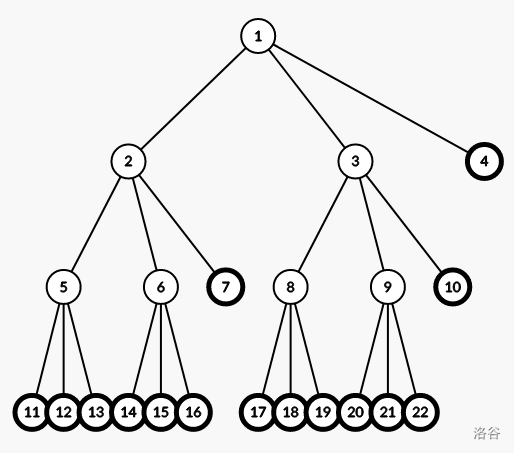
如图为 的情况,删去黑色节点事实上我并不理解为什么到了这一步还推不出正确答案(似乎也没有被卡到这一档部分分的人)。
显然可以快速计算。这个应该小学就会了吧。。。
同时这个也可以解释为什么
注意 的时候有除以 的情况,要特判。代码
真的很短,为什么不去自己写呢?
#include<bits/stdc++.h> #define int long long #define rd(x) x=read() using namespace std; const int mod=1e9+7; inline int read(){int x=0,f=1;char ch=getchar();while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;} int ksm(int x,int y,int z){int ret=1;while (y){if (y&1) ret=(ret*x)%z;x=(x*x)%z;y>>=1;}return ret;} int INV(int x){return ksm(x,mod-2,mod);} int a,b,h; int T; signed main() { rd(T); while (T--) { rd(a);rd(b);rd(h); if (b==1) cout<<(((a-1)*h+a)%mod);else if (a<=b) cout<<ksm(b,h,mod)*a%mod; else cout<<(a*ksm(b,h,mod)%mod+(ksm(b,h,mod)-1)*(a-b)%mod*INV(b-1)%mod)%mod; putchar('\n'); } }
- 1
信息
- ID
- 6021
- 时间
- 1000ms
- 内存
- 250MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
