自动搬运

查看原文

来自洛谷，原作者为

	Flying2018 **

搬运于2025-08-24 22:26:10，当前版本为作者最后更新于2020-11-03 20:49:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意

给定一个长度为 $n$ 的字符串。维护一个由其子串构成的集合。支持插入操作。

定义一个字符串（包括空串）是好的，当且仅当其是集合中 $>k$ 个元素的后缀。

每次插入操作后回答：有几个字符串是好的，最长的好字符串长度是多少。

题解

首先建出后缀自动机。对于这道题，其中有用的部分是后缀自动机的 parent 树。

通过 parent 树的性质，我们知道任何一条点到根的路径代表一个子串。同样，一个子串 $s$ 是另一个子串 $s'$ 的后缀当前仅当 $s$ 在后缀树上的位置是 $s'$ 到根路径上的某个节点/边。

我们试图让所有子串定位到点上。但是定位并不总是成功的，因为有一些点由于只有一个儿子，所以被直接缩去了。这时候我们定位到的是一条边。

所以一个子串要么定位到一个固定的点，要么对应到一条固定边上的一个被“压缩”掉的节点。

具体的定位方式有很多，树上倍增是其中一种。即预处理出后缀树上每个节点往上跳 $i$ 个父亲的结果，然后用类似于倍增 $\text{LCA}$ 的方法实现。

找到每个子串的对应位置后，由于这道题没有强制在线，我们不妨离线读入所有子串，全部插入进后缀树中，被“压缩”掉的节点复原出来，形成一颗新的树。

比如样例建出的树就长这样：

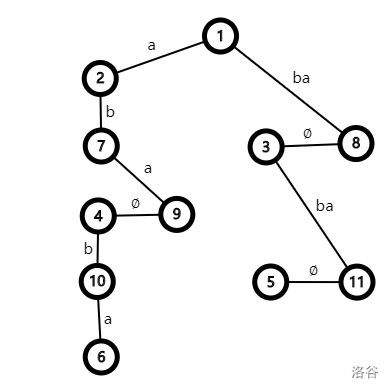
其中 $\varnothing$ 表示的是空串（也就是这两个点应该是在一起的，只是为了方便拆成两个点），点 $1$ 至 $6$ 对应是 parent 树上的点，$7$ 至 $11$ 对应是因询问而插入的点。这里为了方便，对于每一次询问都新建了一个点。这样并不会导致复杂度变劣。

我们定义新树的点权为其表示字符串长度与在后缀树上父亲的长度之差。即 $w_u=len_u-len_{fa_u}$。

可以发现，如果 $u$ 代表的字符串是好的，那么 $u$ 到 $fa_u$ 边上的所有被缩掉点表示的字符串都是好的，总个数就是 $w_u$ 个。

这样原问题就转化为：给定一颗树，每次将一个点染色，定义子树大小是子树中染色点的数量，要求每次操作后输出满足子树大小 $>k$ 的所有点的点权和 与 $len_u$ 的最大值。

随着新点的插入，每个点的子树大小一定是单调不降的。同样，任取树上的一条链，从底向上其子树大小也是单调不降的。

而根据 parent 树的性质，从底向上的 $len_u$ 始终是单调递减的。

所以，对于任何一条链，当我们确定了这条链的最深的点，使得其满足子树大小 $>k$ 后，这条链上所有深度比它小的点都是符合条件的。

同时它的 $len_u$ 也是最长的。所以这样最深的满足条件的点的深度随新点的插入也是单调不降的。

于是我们对新树使用轻重链剖分。即对于一条链我们维护其深度最深的点的位置。一次修改操作对应前缀 $[1,l]\ +1$，每次修改后暴力判断最深的点会不会往下移动。如果会那么暴力更新最深的点的位置，同时修改答案。

为了保证复杂度，修改操作我们要 $O(1)$ 进行。

我们发现最深的点是一步一步向下跳的，考虑差分，先给总权值 $+1$，再给 $l+1$ 位置 $-1$，意思是这次 $+1$ 到 $l+1$ 位置就失效了。每次更新最深的点时加上这个位置的代价即可。

特别的，假如更新位置已经高于最深点位置，这种情况下这次更新不会造成任何影响，直接跳过即可。

由于总链长是 $O(n)$，每次将一个点染色需要跳 $\log n$ 条链，加上预处理时倍增的 $O(\log n)$，总时间复杂度 $O((n+m)\log n)$，空间 $O(n\log n)$。

注意这题有一个坑点，就是如果插入本质相同的子串应当只算一次。这个在插入时特判一下就好了。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<set>
#define ll long long
#define N 1000010
#define D 25
using namespace std;
int nxt[N<<2],to[N<<2],head[N<<1],rcnt;
void add(int u,int v){nxt[++rcnt]=head[u];to[rcnt]=v;head[u]=rcnt;}
int las=1,scnt=1,fa[N<<1],f[N][D],ch[N][26],len[N<<1],acnt,k;
int insert(int c)
{
    int p=las,q=las=++scnt;
    len[q]=len[p]+1;
    for(;p && !ch[p][c];p=fa[p]) ch[p][c]=q;
    if(!p) fa[q]=1;
    else
    {
        int np=ch[p][c];
        if(len[np]==len[p]+1) fa[q]=np;
        else
        {
            int nq=++scnt;
            memcpy(ch[nq],ch[np],sizeof(ch[nq]));
            len[nq]=len[p]+1;
            fa[nq]=fa[np];
            fa[np]=fa[q]=nq;
            for(;p && ch[p][c]==np;p=fa[p]) ch[p][c]=nq;
        }
    }
    return q;
}
int pos[N],nd[N];
vector<int>ad[N];
set<int>s[N];
bool cmp(int a,int b){return len[a]<len[b];}
int work()
{
    int l,r;
    scanf("%d%d",&l,&r);
    int u=pos[r];
    ++acnt;
    len[acnt]=r-l+1;
    for(int i=D-1;i>=0;i--)
        if(f[u][i] && len[f[u][i]]>=len[acnt]) u=f[u][i];
    if(s[u].count(r-l+1)) return 0;//特判重复的插入
    s[u].insert(r-l+1);
    ad[u].push_back(acnt);
    return acnt;
}
void build()
{
    for(int i=2;i<=scnt;i++)
    {
        int p=fa[i];sort(ad[i].begin(),ad[i].end(),cmp);//按长度排序后依次连边即可
        for(int v:ad[i]) add(p,v),p=v;
        add(p,i);
    }
}
int son[N<<1],siz[N<<1],dep[N<<1],ldep[N<<1];
void dfs1(int u)
{
    siz[u]=1;
    ldep[u]=1;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];dep[v]=dep[u]+1;
        fa[v]=u;
        dfs1(v);
        if(siz[v]>siz[son[u]]) son[u]=v;
        siz[u]+=siz[v];
    }
    ldep[u]=ldep[son[u]]+1;
}
int ar[N*20],par;
int* _new(int k){par+=k;return ar+(par-k);}//动态分配内存，减小常数
int* b[N<<1];int g[N<<1],d[N<<1];
int top[N<<1],pp[N<<1];
void dfs2(int u,int topp)
{
    top[u]=topp;
    if(son[u]) dfs2(son[u],topp);
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v!=son[u]) dfs2(v,v);
    }
    if(u==topp) b[u]=_new(ldep[u]+1),pp[u]=u;
}
ll ans;int res;
void upd(int u)
{
    if(dep[u]<dep[pp[top[u]]]) return;
    b[top[u]][dep[u]-dep[top[u]]+1]--;g[top[u]]++;
    u=top[u];
    while(pp[u])
    {
        if(g[u]+b[u][dep[pp[u]]-dep[u]]>k)
        {
            ans+=len[pp[u]]-len[fa[pp[u]]];
            res=max(res,len[pp[u]]);
            g[u]+=b[u][dep[pp[u]]-dep[u]];
            pp[u]=son[pp[u]];
        }
        else break;
    }
}
void ins(int u){for(;u;u=fa[top[u]]) upd(u);}
char str[N];
int main()
{
    int n,m;
    scanf("%d%d%d%s",&n,&m,&k,str+1);
    for(int i=1;i<=n;i++) pos[i]=insert(str[i]-'a');
    for(int i=1;i<=scnt;i++) f[i][0]=fa[i];
    for(int j=1;j<D;j++)
        for(int i=1;i<=scnt;i++) f[i][j]=f[f[i][j-1]][j-1];
    acnt=scnt;
    for(int i=1;i<=m;i++) nd[i]=work();
    for(int i=1;i<=scnt;i++) s[i].clear();
    build();
    len[0]=-1;
    dfs1(1);dfs2(1,1);
    for(int i=1;i<=m;i++)
    {
        if(nd[i]) ins(nd[i]);
        printf("%lld %d\n",ans,res);
    }
    return 0;
}