自动搬运

查看原文

来自洛谷，原作者为

	catandcode 一生所爱，唯猫与代码

搬运于2025-08-24 22:26:05，当前版本为作者最后更新于2023-03-22 20:32:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

计算几何+状压，个人感觉是道好题，用最基础的奇偶变换搞人心态。

Provicy 大佬的思路非常清晰，我的对叉积的优化也来自于他，但像我这样的蒟蒻可能看不懂大佬的题解，所以我来写一篇。第一篇题解，如果有不足还请指出，欢迎 hack。

前置

本题需要运用叉积的知识。

首先是 $O(n^2)$ 的暴力判断，很明显是无法通过的，但我们可以对其进行优化。

由于题目给出全部坐标均为整点，根据叉积公式 $(x_1-x_0)\cdot(y_2-y_0)-(x_2-x_0)\cdot(y_1-y_0)$，可以看出返回叉积值必然为整数，而三角形的面积是叉积的一半。据此，我们可以根据奇偶性判断面积是否为整数，同时也避免了冗杂的计算。

对于输入的整点，可以直接与 $1$ 做与运算，利用前缀和处理面积。

这里先说一下我这里说的前缀和处理一般情况的面积的含义。

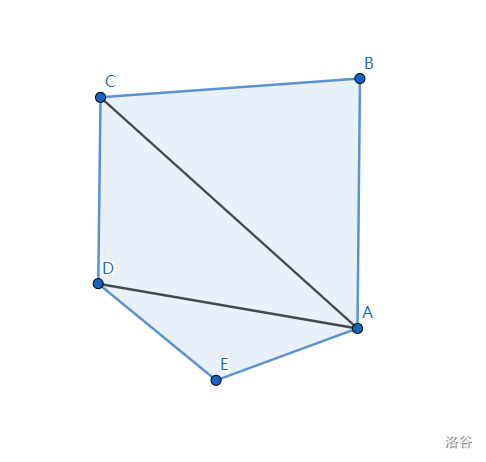
对于这样一个多边形，首先是计算 $AB\times AC$，累加到面积中，然后计算 $AC\times AD$，以此类推，这样对于任意的 $s[i]-s[j]$，计算的就是 $Ai$ 和 $Aj$ 所截面积。

对于任意数据，由于只需要考虑奇偶两种情况，可以对叉积的运算式进行优化。

如果原点坐标（单指横坐标或纵坐标，下同）是偶数，所得向量坐标的奇偶性（相对于终点，下同）是没有改变的，若为奇数，向量的奇偶性相反，但由于是对于两个终点都取反，最后影响可以抵消。对于原公式中的加减法，奇偶相加减得奇，偶偶或奇奇相加减得偶，这恰好和异或运算的规则相同，于是公式可以更改为 $(x_1\cdot y_2)\operatorname{xor}(x_2\cdot y_1)$.

同时时间复杂度的部分优化也在这里。由于我们可以剔除原点的影响，就没有必要分别计算从不同原点出发的前缀和，可以直接用一个前缀和数组表示。

这边要注意一下，原点是要从 $n$ 开始的，这是为了从第一个点开始有面积面积，将第一条边加入计数，当然也可以更改循环，但是这个比较麻烦。我在这里卡了好久 qaq

特判一下整个图形面积为奇数，这种情况显然无解。

DP

由于只考虑奇偶性，我们可以定义一个三维的数组 $dp_{i,j,k}$，$j$ 表示出发点的横坐标，$k$ 表示出发点的纵坐标，$i$ 表示从原点到出发点的面积，在每个顶点考虑之后将其加入 dp 数组。这里我将 $i$ 这一维放到了最后，因为这一维是由出发点坐标和终点时累计面积决定的。逆运算仍然是异或，是不是很神奇， 具体过程可以参考代码。

为了不重复计数，我们对于对角线的一般计数方式是只考虑 $i$ 至 $n$ 的对角线，这也营造了一种类似于单调性的性质。即若倒叙考虑，对于任意一个顶点，只会与前面遍历过的顶点相组合，这也满足了 dp 的一大性质。

但在实现之后会有一个问题，测试输出与样例输出并不吻合，且刚好相差 $n$。

手推一下实现过程，可以发现 $(i,i-1)$ 这一对无序点对是不符合对角线条件的，但是递推仍会将其考虑进去，所以最后 $ans$ 的结果要减去 $n$。

最终时间复杂度 $O(n)$。

代码

冷知识：short 类型的空间占用是小于 bool 类型的。

#include<bits/stdc++.h>
#define ld long double
#define ll long long
#define pre(x) x==1?n:x-1
using namespace std;
int aa,bb;
struct point
{
	short x,y;
	void give(){ x=abs(aa)&1,y=abs(bb)&1; }
	short operator ^(point a){ return (x*a.y)^(a.x*y); }
}p[200005];//个人习惯在结构体中初始化和重载，减少码量
int n;
short sum[200005];
ll ans,dp[2][2][2];
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin>>n;
	for(int i=1;i<=n;++i)
	{
		cin>>aa>>bb;
		p[i].give();
	}
	for(int i=1;i<=n;++i) sum[i]=sum[i-1]^(p[i]^p[pre(i)]);
	if(sum[n]&1) { cout<<0<<endl; return 0; }
	for(int i=1;i<=n;++i)
	{
		for(int j=0;j<=1;++j)
			for(int k=0;k<=1;++k)
			{
				point e=(point){j,k};
				short temp=sum[i]^(p[i]^e);
				ans+=dp[temp][j][k];
			}
		++dp[sum[i]][p[i].x][p[i].y];
	}
	cout<<ans-n<<endl;
	return 0;
}