自动搬运

查看原文

来自洛谷，原作者为

	zhylj 人生输家

搬运于2025-08-24 22:25:47，当前版本为作者最后更新于2022-01-17 19:32:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目

有 $n$ 个竖直放置的塔，第 $i$ 个高度为 $h_i$，你需要将其安装在一个折线上 $(x_1,y_1)-\cdots-(x_m,y_m)$ 的任意实数位置（两个塔可以被安装在相同位置，但此时只有最高的有贡献），使得从左上到右下，与水平地面夹角为 $\alpha\degree$ 的平行光线照到塔上的长度之和最大。

给出最大的长度之和，并构造方案。

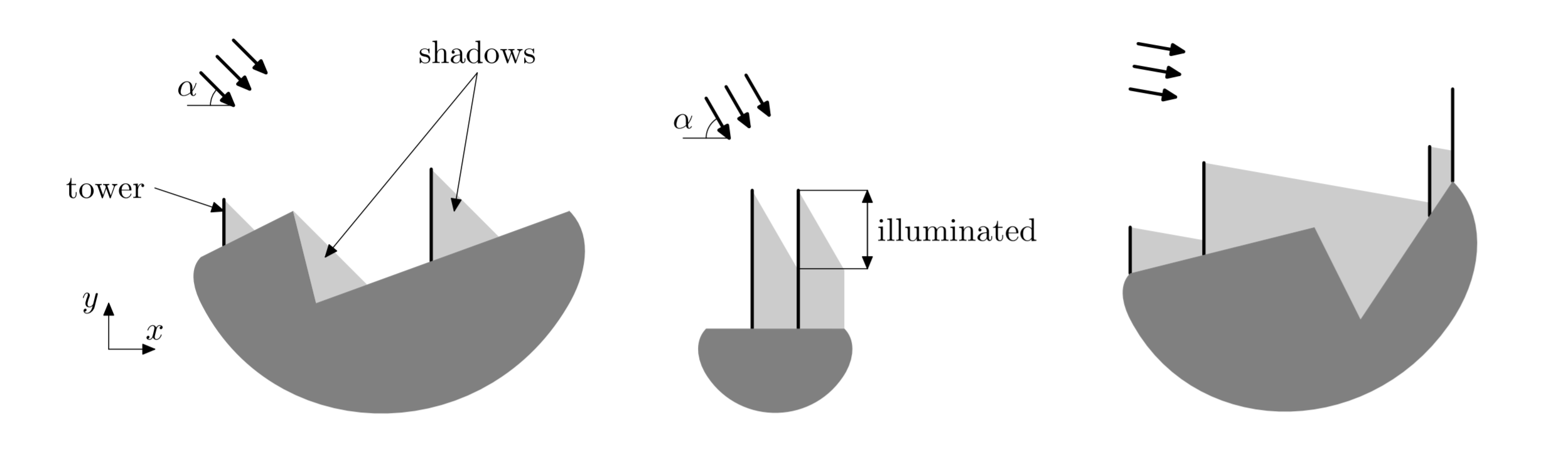
分析

显然可以将最后一个被照到光的塔移到折线的某个端点上使得答案不变劣，不妨设这个塔编号为 $i$，这个端点为 $(x_j,y_j)$。

考虑将所有塔被光照到的部分沿着光线平移至 $x=x_1$ 处，那么塔 $i$ 就在这条线的最高处，并且不难发现，此时最多能被覆盖的长度即为这条线的最高处到 $(x_1,y_1)$ 之间的长度，即存在一个显然的上界为：$\min\{(x_j-x_1)\tan \alpha + y_j - y_1 + h_i,\sum_k h_k\}$，不难发现这个上界是可以取到的，我们只需要先确定最高点后贪心填就可以了。

对于求答案，可以发现上式 $i$ 和 $j$ 的影响是独立的，可以分别枚举最大值然后加起来。

对于构造方案，上面已经说了，确定了最高点后，贪心的在最高点前填使得被光照到的地方尽可能多，然后再尽可能靠前。可以直接在 $x = x_1$ 上填，然后再找与折线的交点。

于是不难做到 $\mathcal O(n + m)$ 的时间复杂度。

代码

typedef long double ff;
const int N = 1e4 + 5;
const ff PI = acos(-1), EPS1 = 1e-20, EPS2 = 1e-6, INF = 1e20;

int n, m, h[N], X[N], Y[N]; ff alpha, pos[N];
ff GetHeight(int i) { return (X[i] - X[1]) * tan(alpha) + (Y[i] - Y[1]); }
ff Ints(int x_0, int y_0, int i) {
	ff k_1 = (Y[i + 1] - Y[i]) / (ff)(X[i + 1] - X[i]), k_2 = -tan(alpha),
		b_1 = -k_1 * X[i] + Y[i], b_2 = -k_2 * x_0 + y_0;
	return (b_2 - b_1) / (k_1 - k_2 + EPS1);
}
bool Check(int x_0, int y_0, int i) {
	ff x_ints = Ints(x_0, y_0, i);
	return x_ints > X[i] - EPS2 && x_ints < X[i + 1] + EPS2;
}

int main() {
	rd(n, m, alpha); alpha *= PI / 180;
	int h_sum = 0, h_mx = 0, h_mx_id = 0;
	for(int i = 1; i <= n; ++i) {
		rd(h[i]); h_sum += h[i];
		if(h[i] > h_mx) {
			h_mx = h[i];
			h_mx_id = i;
		}
	}
	for(int i = 1; i <= m; ++i) rd(X[i], Y[i]);
	ff ans = -INF;
	for(int i = 1; i <= m; ++i) {
		ff i_h = GetHeight(i);
		if(i_h > ans) {
			ans = i_h;
			pos[h_mx_id] = X[i];
		}
	}
	ans += h_mx;
	ans = std::min(ans, (ff)h_sum);
	int cur_y = Y[1];
	for(int i = 1, j = 1; i <= n; ++i) {
		if(i == h_mx_id) continue;
		for(; j < m - 1 && !Check(X[1], cur_y, j); ++j);
		pos[i] = std::max(std::min(Ints(X[1], cur_y, j), (ff)X[m]), (ff)X[1]);
		cur_y += h[i];
	}
	printf("%.15LF\n", ans);
	for(int i = 1; i <= n; ++i)
		printf("%.15LF\n", pos[i]);
	return 0;
}