1 条题解
-
0
自动搬运
来自洛谷,原作者为

zhylj
人生输家搬运于
2025-08-24 22:25:41,当前版本为作者最后更新于2022-01-10 00:09:45,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
考虑对每个平行于圆柱底面的截面,记其到圆柱底面的距离为 ,不妨求出截面上有油的面积 ,然后使用自适应辛普森法求出 即为答案。
我们以截面上圆柱轴与截面的交点为原点,截面上过原点且平行于底面的直线为 轴,过原点且垂直于 轴的直线为 轴建立坐标系,那么不难发现我们只需要求出截面所截得圆的半径以及水面与截面交线在坐标系中的高度即可求得截面上有油部分的面积,我们不妨分开讨论这两个问题:
对于水面与截面交线在坐标系中的高度 :
不妨考虑其与底面的高度 ,那么有:
$$\frac {Y + \frac d2}{h-x\cdot \frac tl} = \frac {l}{\sqrt {l^2-t^2}}\implies Y = \frac {h\cdot l-x\cdot t}{\sqrt {l^2-t^2}} - \frac d2 $$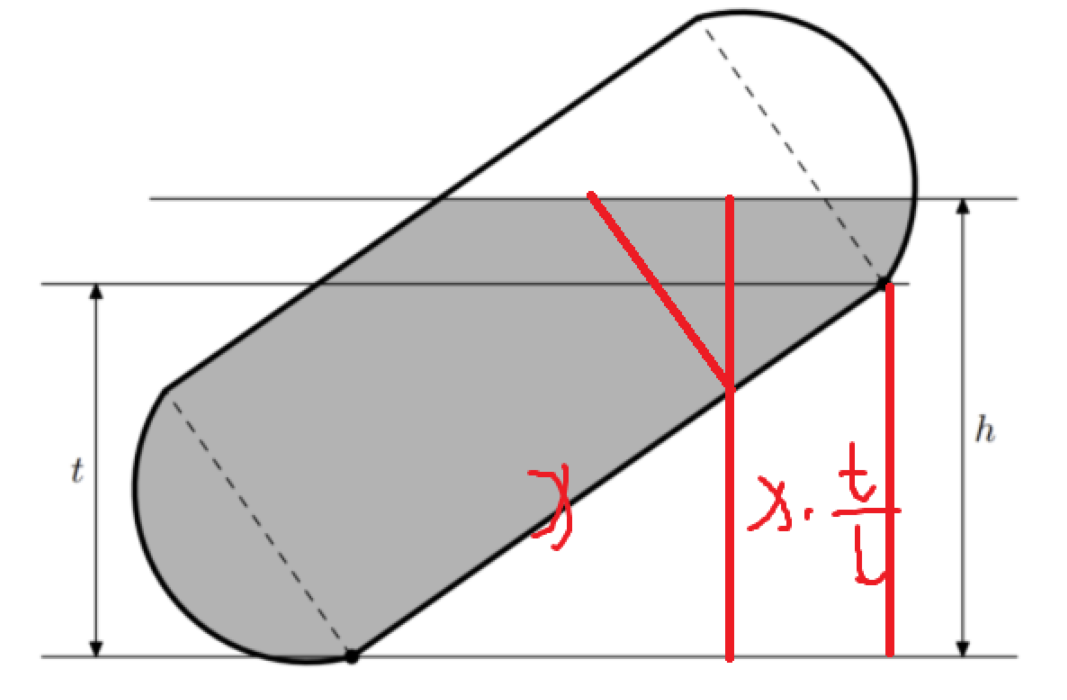
对于所截得圆的半径 ,分两种情况讨论:
-
,那么 。
-
否则求出 超出的部分的长度 或 (根据在左侧或者右侧),然后不难得到:
然后大力积分就做完了。
const ff EPS = 1e-8, INF = 1e5, PI = acos(-1); ff d, l, r, t, h; ff Sq(ff x) { return x * x; } ff F(ff x) { ff l_d = sqrt(Sq(l) - Sq(t)) + EPS; ff Y = (h * l - t * x) / l_d - d / 2, R = 0; if(x > -EPS && x < l + EPS) R = d / 2; else { R = Sq(r) - Sq(sqrt(Sq(r) - Sq(d / 2)) + (x < EPS ? -x : x - l)); if(R < 0) return 0; R = sqrt(R); } ff s_cir = Sq(R) * PI; if(Y > R - EPS) return s_cir; if(Y < -R + EPS) return 0; ff s = sqrt(Sq(R) - Sq(Y)) * Y, s_arc = acos(Y / R) * Sq(R); return s_cir - s_arc + s; } ff Simp(ff L, ff R) { return (R - L) * (F(L) + 4 * F((L + R) / 2) + F(R)) / 6; } ff Asr(ff L, ff R, ff ans, int step) { ff mid = (L + R) / 2, fl = Simp(L, mid), fr = Simp(mid, R); if(fabs(fl + fr - ans) < EPS && step < 0) return (fl + fr + ans) / 2; return Asr(L, mid, fl, step - 1) + Asr(mid, R, fr, step - 1); } ff Solve(ff L, ff R) { return Asr(L, R, Simp(L, R), 12); } int main() { rd(d, l, r, t, h); d /= 100; l /= 100; r /= 100; t /= 100; h /= 100; printf("%.2lf\n", Solve(-r, l + r)); return 0; } -
- 1
信息
- ID
- 6148
- 时间
- 1000ms
- 内存
- 256MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
