自动搬运

查看原文

来自洛谷，原作者为

	_wkjzyc 曲终人散。

搬运于2025-08-24 22:25:39，当前版本为作者最后更新于2020-12-01 13:25:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

先考虑“平坦”且不限次数时的最高高度。此时，除左右端点外皆可+1，相当于通过 $w-2$ 次操作使其变为长 $w-2$ ，高度 $1$ 的新区间。这是一个子问题。最后，得到的序列形如

可以证明这是+1次数最少的方案。而在“不平坦”的序列中，可选一段区间“填平”之后处理。于是得出性质：

• 对于最优解下的操作方案，其最高点向左右皆以 $1$ 每下标的速度下降。

• 若下降时被“阻挡”，之后无需+1操作。

• 若始终不被阻挡，则高度无法达到。

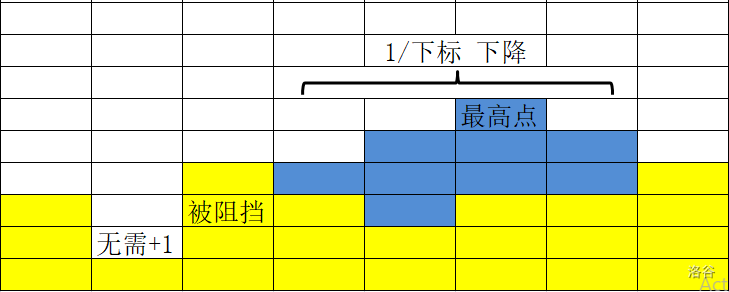
易知最高点单调。对于每个位置二分高度，判断能否达到，以及可达到时所需最少的+1次数。所有位置上二分结果的最大值就是答案。

判断

“被阻挡”相当于此时的蓝色高度低于黄色（原序列）高度。

记最高点 $p$ 高度 $m$ ，若在 $[l,q]$ 区间内（最高点左侧）被阻挡，则可以表达为

等价于

左边RMQ问题可以用st表维护，判断时二分左端点即可。最高点右侧同理。

代码

#include<iostream>
#include<cstdio>
#define int long long
using namespace std;

const int MAXN=1e5+5;
int n,ans,s[MAXN];
int w,h[MAXN];

namespace ST { //预处理
	int lg2[MAXN],l[MAXN][20],r[MAXN][20];
	int QueryL(int i,int j,int num) {
		int tmp=lg2[j-i+1];
		return max(l[i][tmp],l[j-(1<<tmp)+1][tmp])+j-num;
	}
	int QueryR(int i,int j,int num) {
		int tmp=lg2[j-i+1];
		return max(r[i][tmp],r[j-(1<<tmp)+1][tmp])-i-num;
	}
	void Init() {
		for(int i=2;i<=w;i++) lg2[i]=lg2[i-1]+(2<<lg2[i-1]==i);
		for(int i=1;i<=w;i++) l[i][0]=h[i]-i,r[i][0]=h[i]+i;
		for(int i=1;(1<<i)<=w;i++) for(int j=1;j+(1<<i)-1<=w;j++) {
			l[j][i]=max(l[j][i-1],l[j+(1<<(i-1))][i-1]);
			r[j][i]=max(r[j][i-1],r[j+(1<<(i-1))][i-1]);
		}
	}
}

bool Check(int p,int m) { //第二次 二分下标
	int _l,_r,l,r;
	for(l=1,r=p;l<r;) {
		int mid=l+r+1>>1;
		if(ST::QueryL(mid,p,m)>=0) l=mid;
		else r=mid-1;
	}
	if(ST::QueryL(l,p,m)<0) return 0; //必须“被阻挡”
	_l=l;
	for(l=p,r=w;l<r;) {
		int mid=l+r>>1;
		if(ST::QueryR(p,mid,m)>=0) r=mid;
		else l=mid+1;
	}
	if(ST::QueryR(p,l,m)<0) return 0; //必须“被阻挡”
	_r=l;
	if((_r-p)*(2*m-_r+p+1)/2+(p-1-_l)*(2*m-p+_l)/2-s[_r-1]+s[_l]>n) return 0; //操作不多于n次
	return 1;
}

signed main() {
	scanf("%lld%lld",&w,&n);
	for(int i=1;i<=w;i++) scanf("%lld",&h[i]),s[i]=s[i-1]+h[i];
	ST::Init();
	for(int i=1;i<=w;i++) {
		int l=h[i],r=h[i]+n;
		while(l<r) { //第一次 二分高度
			int mid=l+r+1>>1;
			if(Check(i,mid)) l=mid;
			else r=mid-1;
		}
		ans=max(ans,l);
	}
	printf("%lld\n",ans);
	return 0;
}